牛客刷题-Day8
今日刷题:\(1036-1040\)
1036 凸多边形的划分
题目描述
给定一个具有 \(N\) 个顶点的凸多边形,将顶点从 \(1\) 至 \(N\) 标号,每个顶点的权值都是一个正整数。将这个凸多边形划分成 \(N-2\) 个互不相交的三角形,试求这些三角形顶点的权值乘积和至少为多少。
输入描述
输入第一行为顶点数 \(N\)。
第二行依次为顶点 \(1\) 至顶点 \(N\) 的权值。
输出描述
输出仅一行,为这些三角形顶点的权值乘积和的最小值。
示例
输入
5
121 122 123 245 231
输出
12214884
备注
对于 \(100\%\) 的数据,有 \(N≤50\),每个点权值小于 \(10^9\)。
解题思路
- 状态表示:\(f_{i,j}\) 表示将 \([i,j]\) 区间的点划分为 \(j-i-2\) 个三角形的权值乘积和;
- 状态计算:枚举顶点 \(k\in[i+1,k-1]\),这样就可以将 \([i,j]\) 划分为三个区间,则 \(f_{i,j}=max\{f_{i,j},f_{i,k}+f_{k,r}+a_i*a_k*a_j\}\)。
C++ 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 55;template <typename T> void Out(T x) {if(x < 0) putchar('-') , x = -x;if(x > 9) Out(x / 10);putchar(x % 10 + '0');
}int n, a[N];
__int128 f[N][N];int main() {scanf("%d", &n);for (int i = 1; i <= n; i++)scanf("%d", &a[i]);for (int i = 1; i <= n; i++)f[i][i + 2] = (__int128) a[i] * a[i + 1] * a[i + 2];for (int len = 4; len <= n; len++)for (int l = 1; l + len - 1 <= n; l++) {int r = l + len - 1;f[l][r] = 1e30;for (int k = l + 1; k <= r - 1; k++)f[l][r] = min(f[l][r], f[l][k] + f[k][r] + (__int128) a[l] * a[k] * a[r]);}Out(f[1][n]);return 0;
}
1037 [NOIP2003]加分二叉树
题目描述
设一个 \(n\) 个节点的二叉树 \(tree\) 的中序遍历为 \((l,2,3,…,n)\),其中数字 \(1,2,3,…,n\) 为节点编号。每个节点都有一个分数(均为正整数),记第 \(j\) 个节点的分数为 \(d_i\),\(tree\) 及它的每个子树都有一个加分,任一棵子树 \(subtree\)(也包含 \(tree\) 本身)的加分计算方法如下:
\(subtree\) 的左子树的加分\(\times\)\(subtree\) 的右子树的加分\(+\)\(subtree\) 的根的分数
若某个子树为主,规定其加分为 \(1\),叶子的加分就是叶节点本身的分数。不考虑它的空子树。 试求一棵符合中序遍历为 \((1,2,3,…,n)\) 且加分最高的二叉树 \(tree\)。
要求输出:
(1)tree的最高加分
(2)tree的前序遍历
输入描述
第 \(1\) 行:一个整数 \(n\)(\(n<30\)),为节点个数。
第 \(2\) 行:\(n\) 个用空格隔开的整数,为每个节点的分数(分数\(<100\))。
输出描述
第 \(1\) 行:一个整数,为最高加分(结果不会超过 \(4,000,000,000\))。
第 \(2\) 行:\(n\) 个用空格隔开的整数,为该树的前序遍历。
示例
输入
5
5 7 1 2 10
输出
145
3 1 2 4 5
解题思路
- 状态表示:\(f_{i,j}\) 表示节点 \(i\) 到 \(j\) 成树的分数;
- 状态计算:因为只有中序遍历,因此无法确定二叉树的形状,\(i\) 到 \(j\) 的每个点都有可能成为该子树的根节点,因此 \(f_{i,j}=max\{f_{i,j}, f_{i,k-1}*f_{k+1,j}+f_{k,k}\}\)。
C++ 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 50, M = 20010, mod = 998244353;
typedef pair<int, int> PII;
typedef long long LL;int n;
LL f[N][N], root[N][N]; // 从节点 i 到 j 成树的分数void print(int l, int r) {if(l > r) return;printf("%lld ", root[l][r]);print(l, root[l][r] - 1);print(root[l][r] + 1, r);
}int main () {scanf("%d", &n);for(int i = 1; i <= n; i ++) {scanf("%lld", &f[i][i]);f[i][i - 1] = 1; // 左为空f[i + 1][i] = 1; // 右为空root[i][i] = i;}for(int len = 2; len <= n; len ++) {for(int i = 1; i + len - 1 <= n; i ++) {int j = i + len - 1; // 计算终点for(int k = i; k <= j; k ++) {if(f[i][j] < f[i][k - 1] * f[k + 1][j] + f[k][k]) {f[i][j] = f[i][k - 1] * f[k + 1][j] + f[k][k];root[i][j] = k;}}}}printf("%lld\n", f[1][n]);print(1, n);return 0;
}
1038 [NOIP2008]传纸条
题目描述
小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题。一次素质拓展活动中,班上同学安排做成一个 \(m\) 行 \(n\) 列的矩阵,而小渊和小轩被安排在矩阵对角线的两端,因此,他们就无法直接交谈了。幸运的是,他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里,小渊坐在矩阵的左上角,坐标 \((1,1)\),小轩坐在矩阵的右下角,坐标 \((m,n)\)。从小渊传到小轩的纸条只可以向下或者向右传递,从小轩传给小渊的纸条只可以向上或者向左传递。
在活动进行中,小渊希望给小轩传递一张纸条,同时希望小轩给他回复。班里每个同学都可以帮他们传递,但只会帮他们一次,也就是说如果此人在小渊递给小轩纸条的时候帮忙,那么在小轩递给小渊的时候就不会再帮忙。反之亦然。
还有一件事情需要注意,全班每个同学愿意帮忙的好感度有高有低(注意:小渊和小轩的好心程度没有定义,输入时用 \(0\) 表示),可以用一个 \(0-100\) 的自然数来表示,数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条,即找到来回两条传递路径,使得这两条路径上同学的好心程度只和最大。现在,请你帮助小渊和小轩找到这样的两条路径。
输入描述
输入第一行有 \(2\) 个用空格隔开的整数 \(m\) 和 \(n\),表示班里有 \(m\) 行 \(n\) 列(\(1<=m,n<=50\))。
接下来的 \(m\) 行是一个 \(m*n\) 的矩阵,矩阵中第 \(i\) 行 \(j\) 列的整数表示坐在第 \(i\) 行 \(j\) 列的学生的好心程度。每行的 \(n\) 个整数之间用空格隔开。
输出描述
输出共一行,包含一个整数,表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。
示例
输入
3 3
0 3 9
2 8 5
5 7 0
输出
34
备注
\(30\%\) 的数据满足:\(1<=m,n<=10\);
\(100\%\) 的数据满足:\(1<=m,n<=50\)。
解题思路
- 状态表示:\(f_{i,j,p,q}\) 表示从 \((1, 1)\) 到 \((i, j), (p, q)\) 的好心程度,\((i, j)\) 为左下方路径,\((p, q)\) 为右上方路径;
- 状态计算:\(f_{i,j,p,q} = max4(f_{i,j-1,p,q-1}, f_{i,j-1,p-1,q},f_{i-1,j,p,q-1}, f_{i-1,j,p-1,q}) + g_{i,j} + g_{p,q}\),注意不要经过重复的点。
C++ 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 55;int m, n;
int g[N][N];
int f[N][N][N][N]; // f[i][j][p][q] 表示从 (1, 1) 到 (i, j) (p, q) 的好心程度// (i, j) 为左下方路径 (p, q) 为右上方路径 int max4(int a, int b, int c, int d) {return max(max(a, b), max(c, d));
}int main() {scanf("%d%d", &m, &n);for (int i = 1; i <= m; i++)for (int j = 1; j <= n; j++)scanf("%d", &g[i][j]);for (int i = 1; i <= m; i++)for (int j = 1; j < n; j++)for (int p = 1; p <= m; p++)for (int q = j + 1; q <= n; q++)f[i][j][p][q] = max4(f[i][j - 1][p][q - 1], f[i][j - 1][p - 1][q], f[i - 1][j][p][q - 1], f[i - 1][j][p - 1][q]) + g[i][j] + g[p][q];printf("%d\n", f[m][n - 1][m - 1][n]);return 0;
}
1039 [NOIP2000]方格取数
题目描述
设有 \(N*N\) 的方格图(\(N ≤ 10\),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 \(0\)。如下图所示,见样例:
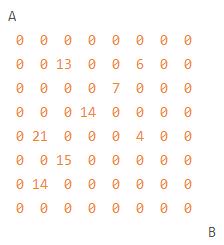
某人从图的左上角的 \(A\) 点出发,可以向下行走,也可以向右走,直到到达右下角的 \(B\) 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字 \(0\))。
此人从 \(A\) 点到 \(B\) 点共走两次,试找出 \(2\) 条这样的路径,使得取得的数之和为最大。
输入描述
输入的第一行为一个整数 \(N\)(表示 \(N*N\) 的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的 \(0\) 表示输入结束。
输出描述
只需输出一个整数,表示 \(2\) 条路径上取得的最大的和。
示例
输入
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
输出
67
解题思路
和 \(1038\) 类似。
C++ 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 15;int n, a[N][N];
int f[N][N][N][N];int max4(int a, int b, int c, int d) {return max(max(a, b), max(c, d));
}int main() {scanf("%d", &n);while (1) {int i, j, v;scanf("%d%d%d", &i, &j, &v);if (i == 0 && j == 0 && v == 0)break;a[i][j] = v;}for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)for (int p = 1; p <= n; p++)for (int q = 1; q <= n; q++) {f[i][j][p][q] = max4(f[i][j - 1][p][q - 1], f[i][j - 1][p - 1][q], f[i - 1][j][p][q - 1], f[i - 1][j][p - 1][q]) + a[i][j] + a[p][q];if (i == p && j == q)f[i][j][p][q] -= a[i][j];}printf("%d\n", f[n][n][n][n]);return 0;
}
1040 [NOIP2005]过河
题目描述
在河上有一座独木桥,一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子,青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数,我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点:\(0\),\(1\),\(……\),\(L\)(其中 \(L\) 是桥的长度)。坐标为 \(0\) 的点表示桥的起点,坐标为 \(L\) 的点表示桥的终点。青蛙从桥的起点开始,不停的向终点方向跳跃。一次跳跃的距离是 \(S\) 到 \(T\) 之间的任意正整数(包括 \(S,T\))。当青蛙跳到或跳过坐标为 \(L\) 的点时,就算青蛙已经跳出了独木桥。
题目给出独木桥的长度 \(L\),青蛙跳跃的距离范围 \(S,T\),桥上石子的位置。你的任务是确定青蛙要想过河,最少需要踩到的石子数。
输入描述
第一行有一个正整数 \(L\)(\(1<=L<=10^9\)),表示独木桥的长度。
第二行有三个正整数 \(S\),\(T\),\(M\),分别表示青蛙一次跳跃的最小距离,最大距离,及桥上石子的个数,其中 \(1<=S<=T<=10\),\(1<=M<=100\)。
第三行有 \(M\) 个不同的正整数分别表示这 \(M\) 个石子在数轴上的位置(数据保证桥的起点和终点处没有石子)。
所有相邻的整数之间用一个空格隔开。
输出描述
只包括一个整数,表示青蛙过河最少需要踩到的石子数。
示例
输入
10
2 3 5
2 3 5 6 7
输出
2
备注
对于 \(30\%\) 的数据,\(L<=10000\);
对于全部的数据,\(L<=10^9\)。
解题思路
P1052 [NOIP 2005 提高组] 过河 题解
需要记住一个结论:定理(\(Frobenius\) 硬币问题,两个变量)
设 \(a\) 和 \(b\) 是两个正整数,且 \(gcd(a,b)=1\)(即互质)。那么,最大的不能表示为 \(ax+by\)(其中 \(x,y\) 是非负整数)的正整数是:\(g(a,b)=ab−a−b\),这个数被称为 \(Frobenius\) 数。
C++ 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 10010, M = 110;int L, S, T, m;
int a[M], dist[M];
int f[N], stone[N];int main() {cin >> L >> S >> T >> m;for (int i = 1; i <= m; i++)cin >> a[i];if (S == T) {int ans = 0;for (int i = 1; i <= m; i++)if (a[i] % S == 0)ans++;cout << ans << endl;return 0;}sort(a + 1, a + m + 1);int DIST = 72;for (int i = 1; i <= m; i++) {int d = a[i] - a[i - 1];if (d >= DIST)dist[i] = dist[i - 1] + DIST;elsedist[i] = dist[i - 1] + d;}for (int i = 1; i <= m; i++)stone[dist[i]] = 1;L = dist[m] + DIST;for (int i = 1; i <= L; i++) {f[i] = 0x3f3f3f3f;for (int j = S; j <= T; j++)if (i >= j)f[i] = min(f[i], f[i - j] + stone[i]);}int ans = 0x3f3f3f3f;for (int i = dist[m]; i <= L; i++)ans = min(ans, f[i]);cout << ans << endl;return 0;
}
