查找基础概念
查找的定义
查找(又称搜索)是从一组数据中,找出 “关键字与目标值匹配” 的记录的操作;若找到则返回记录的位置(如数组下标),若未找到则返回 “不存在” 标识(如-1)。
查找效率的影响因素
- 数据存储特点:数据是否有序、存储结构是顺序表(数组)还是链表,或哈希表等;
- 查找算法本身:算法的时间复杂度(比较次数、操作次数)。
常见查找算法
线性查找(顺序查找)
核心思想
从数据序列的起始位置开始,逐个遍历元素,与目标值逐一比较,直到找到匹配元素或遍历结束。
算法步骤(序列:[3, 9, 8, 2, 1, 4, 6, 5, 7],目标值:6)
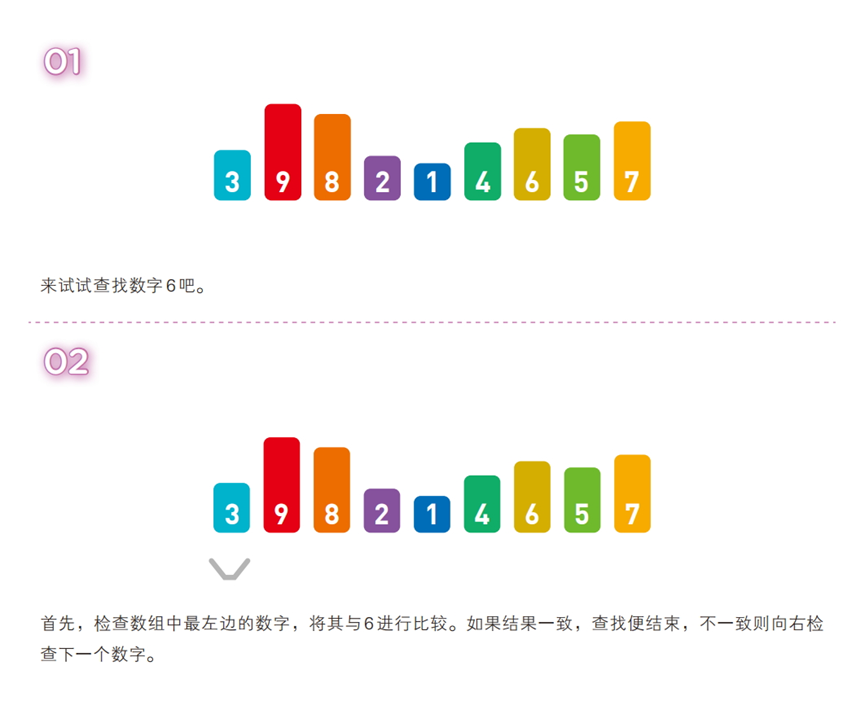
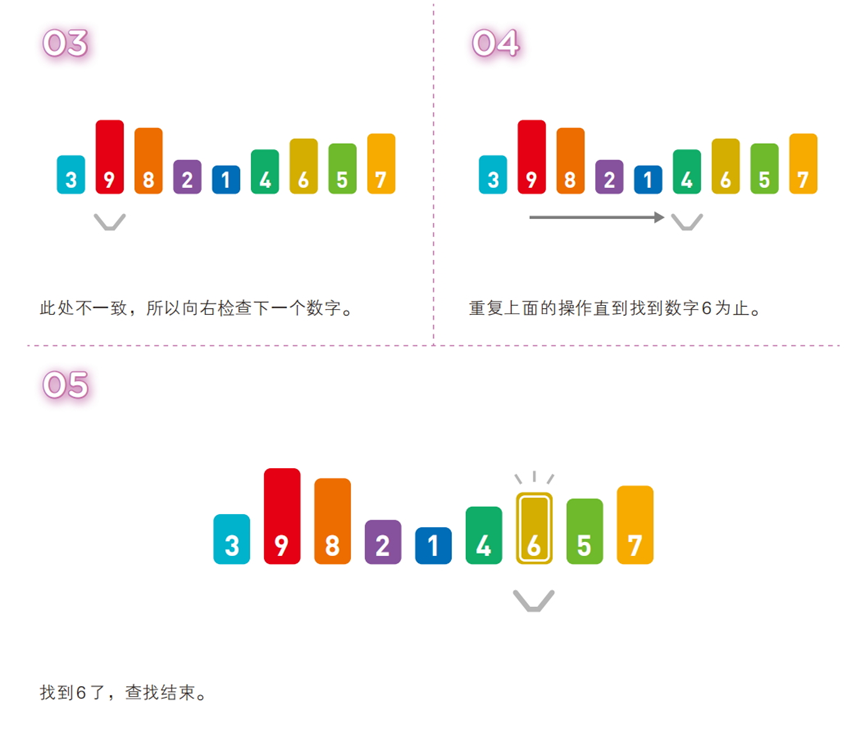
适用场景
- 数据存储结构:顺序表(数组)(通过下标递增遍历)、链表(通过指针
p = p->next遍历); - 数据状态:有序或无序均可(无需预处理)。
时间复杂度
- 最坏情况:
O(n)(目标值在序列末尾,或目标值不存在,需遍历所有元素); - 最优情况:
O(1)(目标值在序列首位)。
优缺点
- 优点:实现简单,无需数据预处理(无序数据也可查);
- 缺点:数据量较大时,效率低(比较次数多)。
代码(C 语言,数组实现)
// arr:待查找数组;size:数组长度;target:目标值;返回值:目标值下标(-1表示不存在)
int LinearSearch(int arr[], int size, int target) {for (int i = 0; i < size; ++i) {if (arr[i] == target) {return i; // 找到,返回下标}}return -1; // 未找到
}
二分查找(折半查找)
核心前提
待查找数据序列必须已排序(升序或降序,本文以升序为例);若无序,需先排序再查找。
核心思想
“从中间找,排除一半”:通过不断将查找区间缩小为原来的一半,快速定位目标值(类似字典查字:先翻中间,确定目标在左半本还是右半本)。
算法步骤(有序序列:[1, 2, 3, 4, 5, 6, 7, 8, 9],目标值:6)
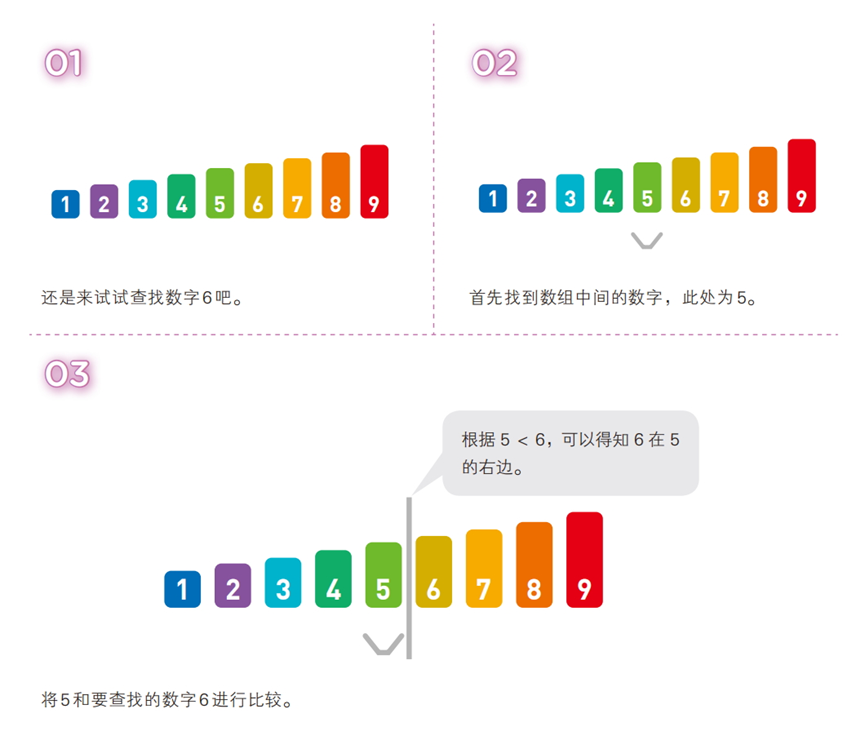
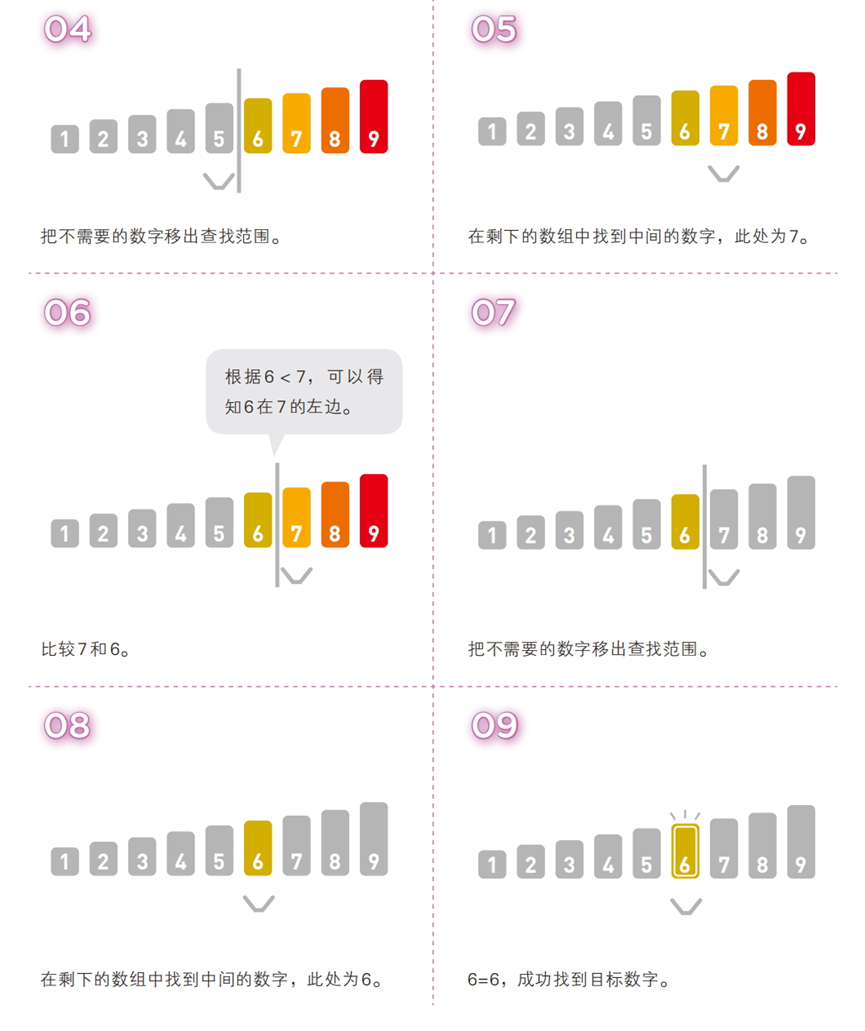
适用场景
二分查找仅适用于顺序表(数组),不适用于链表,链表通过二叉查找树实现二分查找。
时间复杂度
- 每轮排除一半数据,时间复杂度为
O(logn)(如n=1024时,最多仅需 10 次比较,效率远高于线性查找)。
优缺点与选择依据
- 优点:查找速度快(尤其数据量大时);
- 缺点:需数据已排序,且添加元素时需插入合适位置(维护成本高);
- 选择依据:
- 若 “查找操作频繁,添加操作少”(如静态数据:历史成绩表),选二分查找;
- 若 “添加操作频繁,查找操作少”(如动态数据:实时新增的日志),选线性查找。
代码(C 语言,升序数组)
int BinarySearch(int arr[], int size, int target) {int low = 0;int high = size - 1;while (low <= high) {int mid = (low + high) / 2; // 中间位置(避免溢出也可写为low + (high - low)/2)if (arr[mid] == target) {return mid; // 找到,返回下标} else if (arr[mid] < target) {low = mid + 1; // 目标在右半区间} else {high = mid - 1; // 目标在左半区间}}return -1; // 未找到
}
哈希表
当数据量极大时(如百万级用户数据),线性查找和二分查找效率仍不足,此时需用哈希表(又称散列表)—— 一种 “支持快速查找” 的数据结构,查找时间复杂度可接近O(1)。
哈希表基础
- 哈希表的定义
哈希表是一种 “key-value(键值对)” 存储结构,通过一个哈希函数将 “关键字 key” 映射到 “哈希表的索引(地址)”,使每个 key 对应唯一的索引,从而实现 “按 key 快速定位 value”。
- 例:key = 学生学号,value = 学生信息(姓名、分数),通过哈希函数将学号映射到数组下标,直接访问下标即可获取学生信息。
哈希函数(核心)
- 定义:将 key 转换为哈希表索引的函数,记为
H(key); - 要求:计算简单、映射均匀(尽量避免不同 key 映射到同一索引,即 “哈希冲突”);
- 常见哈希函数类型:
- 直接定址法:
H(key) = a*key + b(a、b 为常数);- 例:key = 员工工号(1001,1002,1003),取
a=1,b=-1000,则H(1001)=1,H(1002)=2,直接映射到下标 1、2; - 适用场景:key 范围小且连续。
- 例:key = 员工工号(1001,1002,1003),取
- 除留余数法:
H(key) = key % p(p 为小于等于哈希表长度的最大质数);- 例:哈希表长度 = 10,p=7(小于 10 的最大质数),key=15,则
H(15)=15%7=1,映射到下标 1; - 适用场景:key 范围大且不连续(最常用的哈希函数)。
- 例:哈希表长度 = 10,p=7(小于 10 的最大质数),key=15,则
- 数字分析法:取 key 的 “数字特征明显的部分” 作为索引;
- 例:key = 手机号(138xxxx1234),后 4 位唯一,取
H(key)=后4位,映射到下标 1234; - 适用场景:key 的某部分数字重复率低。
- 例:key = 手机号(138xxxx1234),后 4 位唯一,取
- 直接定址法:
哈希冲突(不可避免)
- 定义:不同的 key 通过哈希函数计算出相同的索引(如
H(7)=0,H(14)=0,key=7 和 14 映射到同一索引 0); - 解决方法:
- 开放定址法:若索引
H(key)已被占用,按一定规则寻找下一个空索引;- 线性探测:
H_i = (H(key) + i) % m(i=0,1,...,m-1;m 为哈希表长度);- 例:哈希表长度 m=10,H (7)=0(已占用),则 i=1 时
H_1=(0+1)%10=1,若 1 空则存 1,否则 i=2 找 H_2=2,以此类推;
- 例:哈希表长度 m=10,H (7)=0(已占用),则 i=1 时
- 二次探测:
H_i = (H(key) + i²) % m(避免线性探测的 “聚集问题”,即连续占用);
- 线性探测:
- 链地址法:将映射到同一索引的 key,用链表串联起来;
- 例:哈希函数
H(key)=key%3,key=1、4、7,H(1)=1,H(4)=1,H(7)=1,则在索引 1 处存储链表:1 → 4 → 7; - 优点:无聚集问题,处理冲突效率高(最常用的冲突解决方法)。
- 例:哈希函数
- 开放定址法:若索引
哈希查找
核心思想
通过哈希函数计算目标 key 的索引,直接访问该索引:
- 若索引对应位置为空:目标 key 不存在;
- 若索引对应位置有数据:比较 key 是否匹配,匹配则返回 value;若不匹配(哈希冲突),按冲突解决方法遍历查找。
算法步骤(以链地址法为例,哈希表:索引 0→[0,3,6],索引 1→[1,4,7],索引 2→[2,5,8],目标 key=4)
- 计算哈希函数:
H(4)=4%3=1,确定索引 1; - 访问索引 1 的链表,遍历链表元素
1、4; - 找到 key=4,匹配成功,返回对应的 value;
- 若目标 key=9:
H(9)=9%3=0,访问索引 0 的链表[0,3,6],遍历后无 9,返回 “不存在”。
时间复杂度
- 理想情况(无哈希冲突):
O(1)(直接访问索引); - 实际情况(有冲突):
O(1 + α)(α 为 “负载因子”,即哈希表中元素个数 / 哈希表长度,α 越小,冲突越少,效率越高,通常 α 控制在 0.7 以下)。
优缺点与适用场景
- 优点:查找速度极快(接近 O (1)),适合大规模数据;
- 缺点:哈希函数设计复杂、需处理冲突、内存占用可能较高(需预留哈希表空间);
- 适用场景:高频查找、大规模数据(如数据库索引、缓存系统、用户信息查询)。
代码C 语言,链地址法哈希表)
- 定义
typedef struct Node {int key;int value;struct Node* next;
} Node;// 哈希表(数组+链表,size为数组长度)
typedef struct HashTable {int size;Node** table;
} HashTable;
- 初始化
// 初始化哈希表
HashTable* initHashTable(int size) {HashTable* ht = (HashTable*)malloc(sizeof(HashTable));ht->size = size;// 初始化数组,每个元素为NULL(空链表)ht->table = (Node**)calloc(size, sizeof(Node*));return ht;
}
- 哈希函数
// 哈希函数(除留余数法,p为小于size的最大质数,此处简化取size)
int hashFunc(int key, int size) {return key % size;
}
- 插入
// 插入键值对到哈希表
void insert(HashTable* ht, int key, int value) {int idx = hashFunc(key, ht->size);// 创建新节点Node* newNode = (Node*)malloc(sizeof(Node));newNode->key = key;newNode->value = value;newNode->next = NULL;// 链地址法:新节点插入链表头部if (ht->table[idx] == NULL) {ht->table[idx] = newNode;} else {newNode->next = ht->table[idx];ht->table[idx] = newNode;}
}
- 查找
// 哈希查找(返回value,未找到返回-1)
int hashSearch(HashTable* ht, int key) {int idx = hashFunc(key, ht->size);Node* p = ht->table[idx]; // 指向对应索引的链表头// 遍历链表查找keywhile (p != NULL) {if (p->key == key) {return p->value; // 找到,返回value}p = p->next;}return -1; // 未找到
}
