在计算机科学中,Floyd-Warshall算法是一种在具有正或负边缘权重(但没有负周期)的加权图中找到最短路径的算法。算法的单个执行将找到所有顶点对之间的最短路径的长度(加权)。 虽然它不返回路径本身的细节,但是可以通过对算法的简单修改来重建路径。 该算法的版本也可用于查找关系R的传递闭包,或(与Schulze投票系统相关)在加权图中所有顶点对之间的最宽路径。———————百度百科
Floyd算法是一种全源最短路算法,它可以求出任意两点之间的最短路径,相对于Dijkstra算法,它的代码可读性高,简单易写,而且Dijkstra是单源最短路(即求的最短路都是以以同一个点为起点的),但由于Floyd算法的时间复杂度为\(O(n^3)\),所以对于点数太多的图来说不推荐使用。
定义\(f[i][j]\)为从i点到j点的最短距离。简单来说,Floyd使用了动态规划的思想,每次枚举一个\(k\)点作为中间点,算出起点经过\(k\)点到终点的距离,当前答案作比较,不断更新当前答案。
具体:
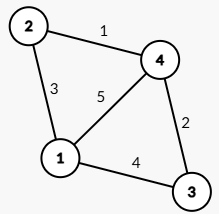
\(给出一个无向图\)
\(此图数据:\)
\(4\;5\)
\(1\;2\; 3\)
\(2 \;4 \;1\)
\(1\; 4 \;5\)
\(4\; 3 \;2\)
\(1\; 3 \;4\)
\(我们使用邻接矩阵来存储\)
\(记f[i][j]为从i点到j点的最短距离,那么我们首先要初始化f[i][j]\)
1.初始化:
\(\qquad输入点数n,边数m\)
\(\qquad每个点到自己的距离肯定为0,所以我们要在i==j的时候让f[i][j]=0\)
\(\qquad其余的f[i][j],由于此时没有添加边,所以各个点目前都没有连通,所以点与点之间现在到达不了彼此。\)
\(\qquad故我们可以初始化成一个很大的数,代表不连通,比如说1e9,或者0x7FFFFFFF等\)
\(\qquad容易写出如下代码:\)
for (int i = 1;i <= n;i ++)for (int j = 1;j <= n;j ++){if (i == j) continue ;f[i][j] = 1e9;}
\(现在我们得到了f=\begin{bmatrix}0 & 1e9 & 1e9 & 1e9\\1e9 & 0 & 1e9 & 1e9\\1e9 & 1e9 & 0 & 1e9\\1e9 & 1e9 & 1e9 & 0
\end{bmatrix}\)
2.输入/连边:
\(\qquad输入了m组u\;v\;w,由于是无向图,所以我们让f[u][v]=f[v][u]=\min(w,f[u][v]),\)
\(\qquad那为啥是\min(w,f[u][v])呢?\)
\(\qquad第一,我们初始化了每两个点之间的距离为1e9,添加的边的权值肯定要比我们设的这个值要小。\)
\(\qquad第二,可能会有重边的情况,这个时候我们肯定要选取更短的那条边。\)
\(\qquad容易写出如下代码:\)
while (m --){int u, v, w;cin >> u >> v >> w;f[u][v] = f[v][u] = min(w, f[u][v]);
}
\(然后,我们就得到了f=\begin{bmatrix}0 & 3 & 4 & 5\\3 & 0 & 1e9 & 1\\4 & 1e9 & 0 & 2\\5 & 1 & 2 & 0
\end{bmatrix}\)
3.核心部分:
for (int k = 1;k <= n;k ++)for (int i = 1;i <= n;i ++)for (int j = 1;j <= n;j ++)f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
\(\qquad我们要把每个点作为中间点k进行答案的更新,具体就是每次将通过k点到达终点的距离与当前保存的距离作比较,选取小的那个\)
\(\qquad易得:当前存储的距离为f[i][j],通过k点到达终点的距离为f[i][k]+f[k][j](重点理解)\)
\(\qquad所以我们容易得到式子f[i][j]=\min(f[i][j],f[i][k]+f[k][j])\)
\(\qquad我们将这段代码的效果部分演示一下:\)

\(\qquad当k=1时:1\rightarrow2=\min(1\rightarrow2,1\rightarrow1+1\rightarrow2)=\min(3,0+3)=3\)
\(\qquad······\)
\(\qquad2\rightarrow3=\min(2\rightarrow3,2\rightarrow1+1\rightarrow3)=\min(1e9,3+4)=7\)
\(\qquad······\)
\(\qquad k=2时\)
\(\qquad······\)
\(\qquad1\rightarrow4=\min(1\rightarrow4,1\rightarrow2,2\rightarrow4)=\min(5,3+1)=4\)
\(\qquad······\)
\(\qquad最终,我们的答案矩阵为变成f=\begin{bmatrix}0 & 3 & 4 & 4\\3 & 0 & 3 & 1\\4 & 3 & 0 & 2\\4 & 1 & 2 & 0
\end{bmatrix}\)
4.输出答案
for (int i = 1;i <= n;i ++){for (int j = 1;j <= n;j ++)cout << f[i][j] << ' ';cout << '\n';
}
完整代码:
#include <iostream>
#include <cmath>
using namespace std;
const int maxn = 1e2 + 5;
int f[maxn][maxn], n, m;
int main(){cin >> n >> m;for (int i = 1;i <= n;i ++)for (int j = 1;j <= n;j ++){if (i == j) continue ;f[i][j] = 1e9;}while (m --){int u, v, w;cin >> u >> v >> w;f[u][v] = f[v][u] = min(w, f[u][v]); }for (int k = 1;k <= n;k ++)for (int i = 1;i <= n;i ++)for (int j = 1;j <= n;j ++){f[i][j] = min(f[i][j], f[i][k] + f[k][j]); }for (int i = 1;i <= n;i ++){for (int j = 1;j <= n;j ++)cout << f[i][j] << ' ';cout << '\n'; } return 0;
}
\(可AC通过洛谷B3647:\)B3647 【模板】Floyd
\(下面我们可以简单应用一下floyd:\)
传递闭包问题(洛谷P3611)
B3611 【模板】传递闭包

\(数据范围1\leq n\leq 100,可以使用Floyd算法。\)
\(读题后我们发现,这道题并不是求最短路径,而是求连通性问题,那么如何用Floyd实现呢?\)
\(实际非常简单,主要是修改核心代码中的数据处理部分:\)
\(·如果这两个点直接就是连通的(f[i][j]==1),那么我们就可以不做修改\)
\(·如果这两个点中间经过k点后可以连通(也就是i到k,k到j都要等于1),那么我们也让此时的f[i][j]=1\)
\(可以写出代码:\)
for (int k = 1;k <= n;k ++)for (int i = 1;i <= n;i ++)for (int j = 1;j <= n;j ++)if (f[i][k] && f[k][j]) f[i][j] = 1;
\(最终代码:(可AC通过)\)
#include <iostream>
using namespace std;
const int maxn = 1e2 + 5;
int f[maxn][maxn], n;
int main(){cin >> n;for (int i = 1;i <= n;i ++)for (int j = 1;j <= n;j ++)cin >> f[i][j];for (int k = 1;k <= n;k ++)for (int i = 1;i <= n;i ++)for (int j = 1;j <= n;j ++)if (f[i][k] && f[k][j]) f[i][j] = 1;for (int i = 1;i <= n;i ++){for (int j = 1;j <= n;j ++)cout << f[i][j] << ' ';cout << '\n';}return 0;
}
\(下面我们再来看一道题:\)
[USACO08OPEN] Clear And Present Danger S(洛谷P2910)
P2910 [USACO08OPEN] Clear And Present Danger S
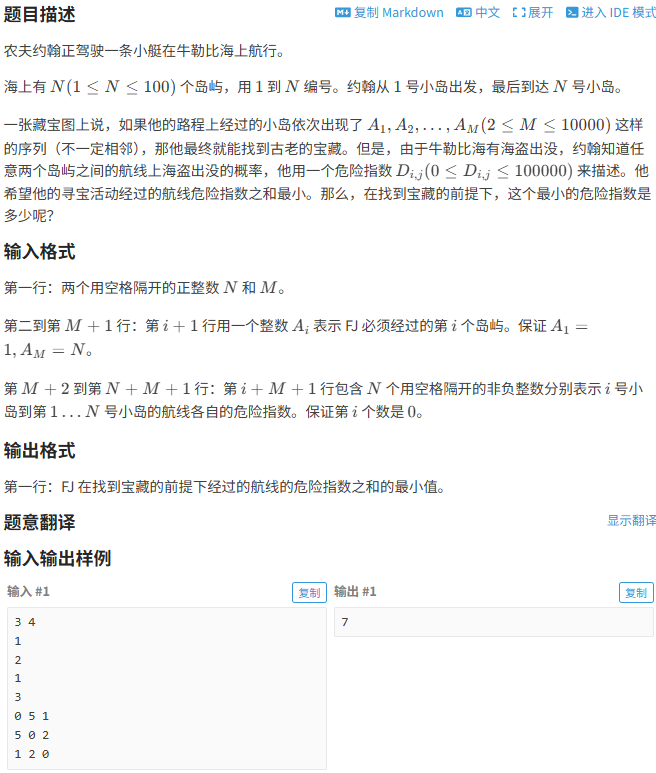
\(发现1\leq N\leq 100,可以使用Floyd\)
\(读题发现,这道题要求的最短路,是必须经过所有a_i的一条路径\)
\(如何求出经过所有a_i的一条最短路径呢?\)
\(可以想到把这一条路径拆成多条路径,即每个a_i\rightarrow a_{i+1}的最短路径,然后全都加起来。\)
\(定义一个ans变量,赋初值为0\)
\(在最后数据处理完成的时候,将我们所说的那些路径长度全都加起来。\)
\(即\)ans += f[a[i-1]][a[i]];
\(完整代码:\)
#include <iostream>
#include <cmath>
using namespace std;
const int maxn = 1e2 + 5;
int f[maxn][maxn], n, m, ans=0, a[10005], w;
int main(){cin >> n >> m;for (int i = 1;i <= m;i ++) cin >> a[i];for (int i = 1;i <= n;i ++)for (int j = 1;j <= n;j ++){if (i == j) continue ;f[i][j] = 1e9;}for (int i = 1;i <= n;i ++)for (int j = 1;j <= n;j ++){cin >> w;f[i][j] = f[i][j] = min(f[i][j], w);}for (int k = 1;k <= n;k ++)for (int i = 1;i <= n;i ++)for (int j = 1;j <= n;j ++)f[i][j] = min(f[i][j], f[i][k] + f[k][j]);for (int i = 2;i <= m;i ++)ans += f[a[i-1]][a[i]];cout << ans;return 0;
}
