好题!
首先是网络流。
此处求的是最小值,一般是最小割或者总值减去最大流。
但是最大流的话,扣去取 max 的东西不是很好维护。而且本质上是要把操作分给两侧,可以用最小割,于是我们考虑最小割!
首先,我们对于每个位置要取 max 而不是 min 不能用最小割的最小算上,所以在一个数轴上进行限制与决策,套路就是把数轴建出来。
把数轴建出来之后呢我们有两个方向,一个是将答案刻画为割掉的边的数量,但这样每一个限制都要连 \(O(V)\) 条边,太多了显然会 T 飞。
另一种方法是列出每个数的每一个选择,然后用最小割选同时满足几个 \(\ge x\) 的条件且最小的那一个,就是最大值。
对于这种方法我们发现相当好维护,我们每一个限制只需要连数轴上的点到另一侧的答案连一条 \(\infin\) 的边就行啦。
考虑限制,对于限制我们最小割一定是建一个虚点,这个虚点放到一边就算上割掉另一边的贡献。但我们的限制条件是取 max,相当于就是放到一边就要满足一个条件。
对于这种情况我们回忆 max 的限制是怎么做的,本质上是连 \(\infin\) 的边到 \(T\) 对不对?但具体结构并不重要,重要的是连通性。于是如果一个强制与 \(T\) 相连的点,我们也可以直接连到这个点对不对。
唉这个点不就是虚点吗!我们可以像虚点连 \(\infin\) 的边!再从虚点连 \(\infin\) 的边到 \(y\) 的那一侧,如果这个虚点割到了一边,那另一边就要相当于连到了 \(T\) 一个无穷边!
但是因为要这样限制,所以我们要把 \(y\) 那一侧的数轴方向颠倒一下,不然就变成限制最小值了。
这样就做完啦!我放一张 \(n=1\) 的示意图!
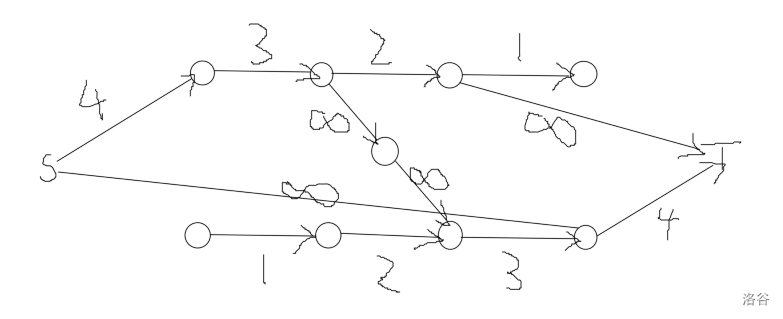
init();
cin >> n >> m;
s = ++cnt;
t = ++cnt;
rep (i, 1, n)rep (j, 1, V)idx[i][j] = ++cnt;
rep (i, 1, n)rep (j, 1, V)idy[i][j] = ++cnt;
rep (i, 1, n) {rep (j, 1, V - 1)add_edge(idx[i][j + 1], idx[i][j], j);add_edge(s, idx[i][V], V);
}
rep (i, 1, n) {rep (j, 1, V - 1)add_edge(idy[i][j], idy[i][j + 1], j);add_edge(idy[i][V], t, V);
}rep (i, 1, n) {int x;cin >> x;add_edge(idx[i][x], t, INF);
}
rep (i, 1, n) {int y;cin >> y;add_edge(s, idy[i][y], INF);
}
rep (i, 1, m) {int cur = ++cnt;rep (j, 1, n) {int a;cin >> a;add_edge(idx[j][a], cur, INF);add_edge(cur, idy[j][a], INF);}
}
cout << Flow::dinic() << endl;
