最近在看卫星通信,在学习星地链路传输的时候看到以下内容
对于频率低于 1 GHz 的频段,使用有源接收面积接收电波时效率提升很困难
频率较低时,波长较长,小口径天线有效接收面积(有效口径)反而较小
有源接收面积 \(A_{c}\) 有以下公式:
这是由增益反向推导出来的,增益为
看这个公式的推导,一直没找到,某某dn网站都要付费,然后我也翻了下那位作者推荐的书目,结合书本和一点点理解做了下推导
推导如下:
对于一个典型的天线,有如下传播场景,Figure 1 为天线方向图
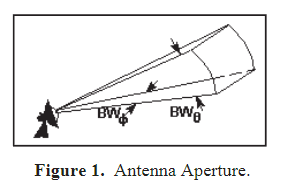
其中 \(BW_{\varphi}\) 为方位角波束宽度(横向波束宽度,the azimuth beamwidth),\(BW_{\theta}\) 为仰角波束宽度(纵向波束宽度,the elevation beamwidth), 一般情况下,波束宽度在半功率点或-3 dB 处测量得到,需要说明的是,该宽度是以角度的方式来度量
而天线(对于某个方向而言)增益(也可以理解为对该方向的指向性,directivity)是该特定方向的辐射强度(该区域的能量值)比上每个方向上的辐射密度的平均值(平均在各个方向上的平均能量值 ),可以由下式表示
对于指向性和增益:
值得说明的是,指向性(Directivity)与增益(Gain)经常被等价替换,但是指向性仅基于天线图案形状进行评估,忽略了天线损耗包括介电(dielect,指可被电极化的绝缘体)、阻抗、极化失配。
如果在计算天线增益时考虑这些损耗,则天线增益就被称为功率增益。
另外,如果在天线系统增益估算中考虑了阻抗失配问题和驻波比损耗,则该天线增益计算结果被称为放大增益(Realized Gain)。
当然,使用指向性(Directivity)对于一阶理想化天线性能的计算估计非常方便
利用综合的总功率对天线各个方向上的辐射功率进行归一化,就可以得到对应天线的指向性,指向性的归一化问题暂不讨论,具体见前文所述的书 3-1.2 中的内容
增益与辐射的角度或范围(辐射方向的投影覆盖角度或范围)大小有关,若辐射角度为所有方向,不妨设此时的增益为 0 dB,若此时角度缩小为近辐射一个半球(面积缩小了一半),此时的增益应当为 3 dB
另外,增益与实际输出功率、半径(测量点与信号源的距离)两个条件无关
假设天线的辐射模式是均匀辐射的(均匀的向任何方向发射信号,各向同性),则某方向的整个各向同性球面的面积比上天线增益为该方向的横截面积(接收到信号的面积),即:
那么对于增益而言,有
由于在特定方向上,都对于每个波源而言,都存在某个相位差为 \(\lambda /2\) 的对应点时,此时会存在干扰使得该方向上存在一个 null 点,即能量抵消,其中第一个 null 点由下列条件限定:
对于小角度而言,用近似的方法可以知道:
其中,如下图所示,\(L\) 是辐射出去的球面上的某一各线段,其垂直于线段上任意一点与信号源的连线(即红笔描出来的线,虽然这根线不一定在三维坐标系上是直线,但是应该不妨碍这样理解)
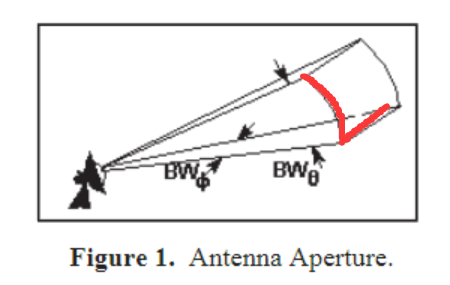
角度 \(\theta\) 是辐射模式中心(最大值)到第一个 null 的角度, null 至 null 波束宽度为 \(2\theta\)。
事实上,对于半功率点(-3 dB 点)而言,这个波束宽度大约是 null 到 null 波束宽度的二分之一,即:
此时增益为:
其中,接收有效面积 \(A_{c}=L_{azimuth}\cdot L_{elevation}\),且
参考书目:
通过网盘分享的文件:Electronic Warfare and Radar Systems Engineering Handbook.pdf
链接: https://pan.baidu.com/s/1h_bk4-ohJOEpC2SihC_JIw?pwd=wncg 提取码: wncg
一开始看到的网站:https://blog.csdn.net/little_soldier/article/details/124209332
