函数逼近(Function Approximation)
此前介绍的所有方法都是表格方法(tabular methods),即为每个状态–动作对存储一个值:要么是该动作的 Q 值,要么是该动作的偏好值。
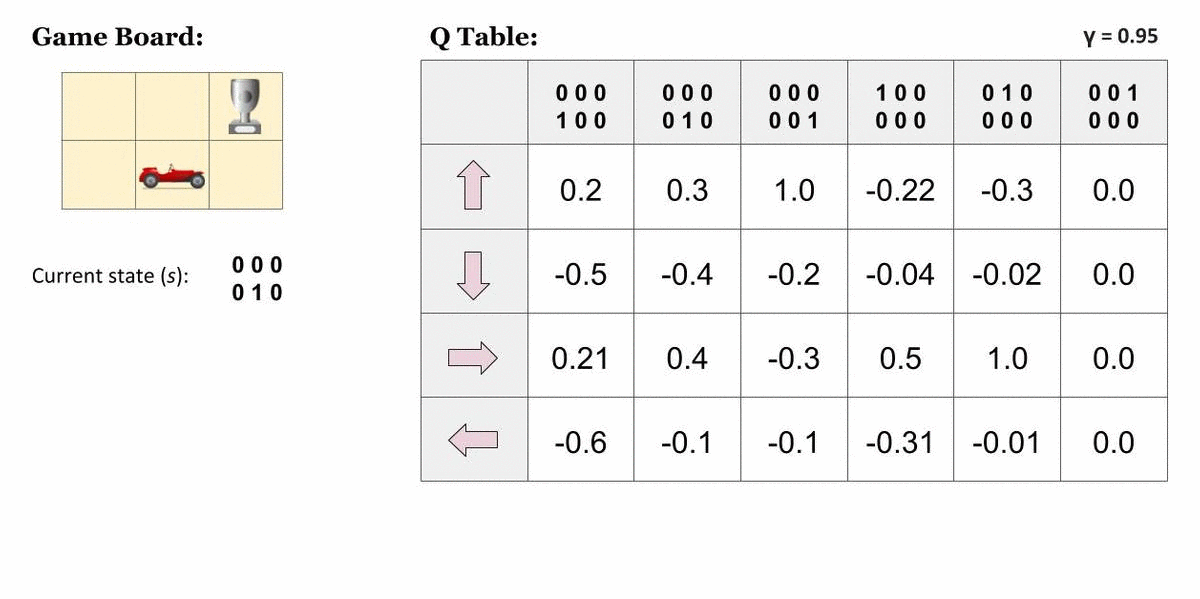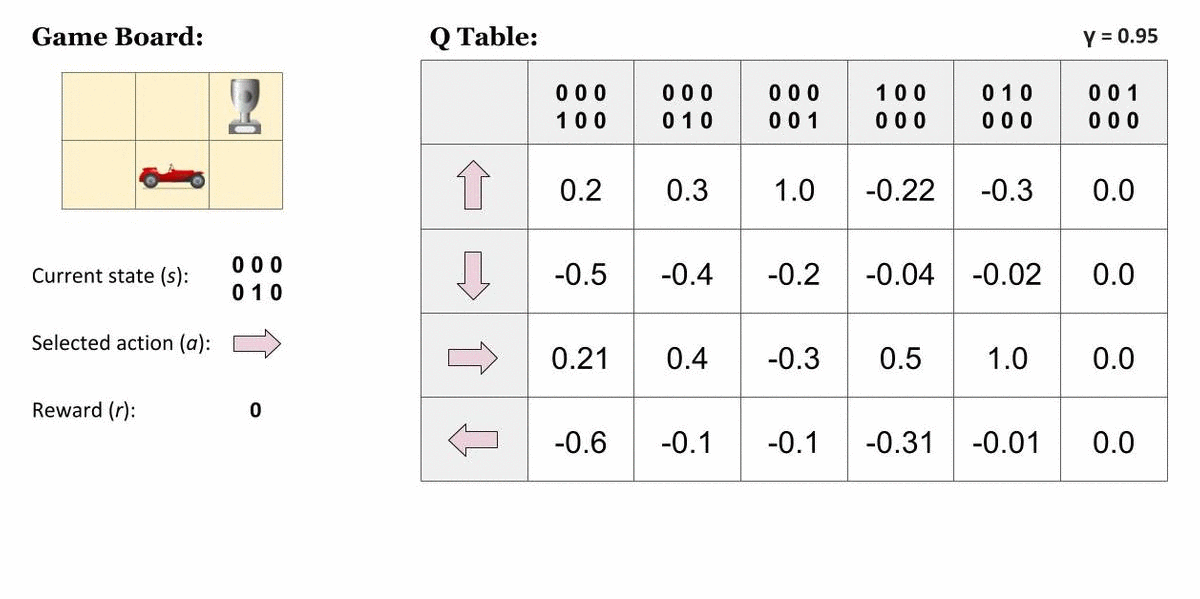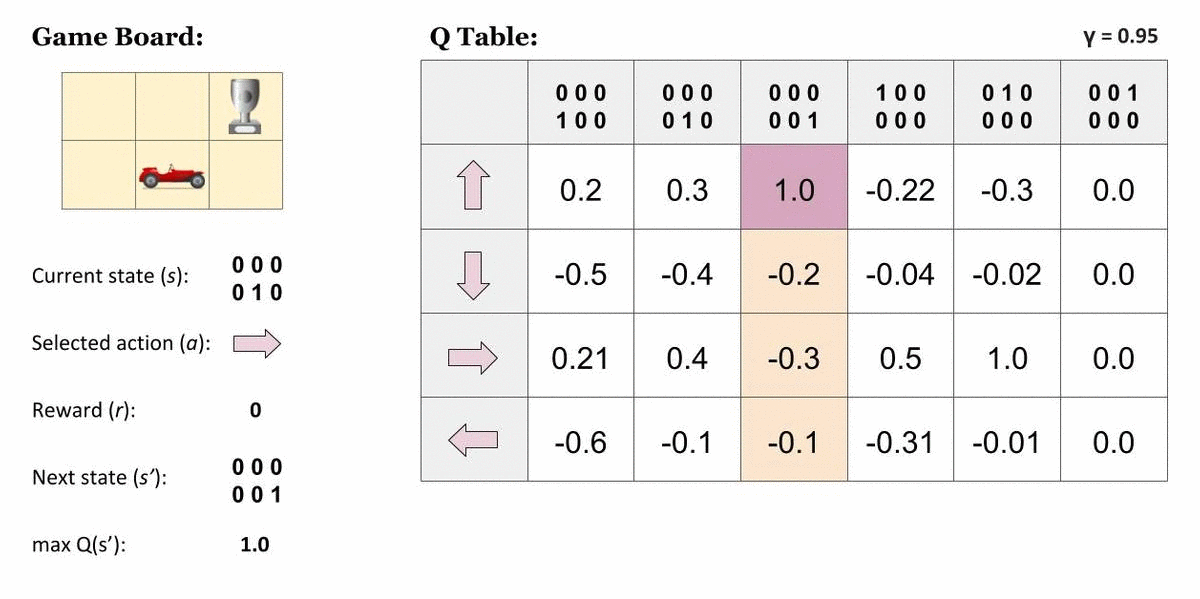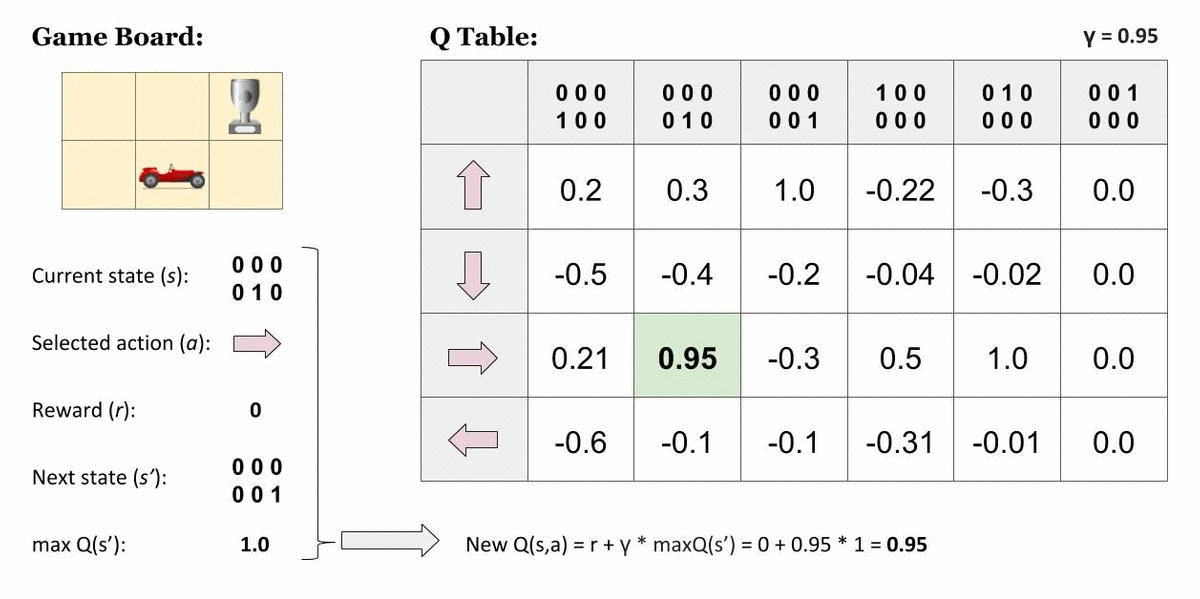
在大多数实际应用中,这样存储的值数量会迅速变得无法处理。例如当输入为原始图像时,可能的状态数目本身就是天文级的。此外,这些算法要求每个状态–动作对都被访问足够多次,才能收敛到最优策略;如果某个状态–动作对从未访问过,则无法保证找到最优策略。在连续状态或动作空间中,这一问题更加明显。
然而,在许多情况下,两个非常相似的状态下应采取的最优动作往往是相同的。例如在视频游戏中改变一个像素通常不会影响最佳动作。因此,若能在不同状态间插值 Q 值将极其有用:只需探索部分状态–动作对,其余的值可通过状态或动作间的相似性泛化(generalization)得到。这就是知识迁移问题,即如何将已学知识推广到未见但相似的情况。
这正是函数逼近(Function Approximation, FA)的用武之地:值函数或策略不再以表格形式存储,而是通过一个函数逼近器进行学习。
逼近器的类型不限:在深度强化学习中通常使用神经网络,但任何可微的回归模型(线性模型、径向基函数网络、支持向量回归等)都可以。
基于值的函数逼近(Value-based Function Approximation)
状态值函数逼近
用一个 \(d\) 维特征向量 \(\phi(s) = [\phi_1(s), \phi_2(s), \ldots, \phi_d(s)]^T\) 表示状态 \(s\)。
以“倒立摆(Cartpole)”为例:
其中 \(x\) 为小车位置,\(\theta\) 为杆角,\(\dot{x}\) 与 \(\dot{\theta}\) 为其导数。这样即可表示任意状态 \(s\)。
对于图像型输入,可以将像素展平为向量。更复杂的场景应包含所有必要信息以保证满足马尔可夫性质。
我们希望用一个参数化函数 \(V_\varphi(s)\) 来逼近真实的状态值函数 \(V^\pi(s)\):
该函数由参数 \(\varphi\) 控制,用于将特征向量 \(\phi(s)\) 映射为近似值 \(V_\varphi(s)\)。
最简单的逼近器是线性逼近器(Linear Approximator):
其中权重向量 \(\mathbf{w} = [w_1, w_2, \ldots, w_d]^T\) 即参数集 \(\varphi\)。
无论函数形式如何,我们希望找到参数 \(\varphi\) 使 \(V_\varphi(s)\) 尽可能接近 \(V^\pi(s)\)。
这就是一个回归问题,目标是最小化均方误差(MSE):
若假设函数可微,则可用梯度下降法(Gradient Descent, GD)迭代优化:
展开梯度形式:
由于计算整个状态空间的期望过于耗时(批量算法),采用随机梯度下降(SGD):
此时参数更新是随机的,噪声较大。
得到的更新规则与线性回归的“Delta 规则”一致,只需能计算 \(\nabla_\varphi V_\varphi(s)\)。
但问题在于我们并不知道真实值 \(V^\pi(s)\)。可用采样估计替代:
- 蒙特卡罗(Monte Carlo)函数逼近:\[\Delta \varphi = \eta (R_t - V_\varphi(s)) \nabla_\varphi V_\varphi(s) \]
- 时间差分(TD)函数逼近:\[\Delta \varphi = \eta (r_{t+1} + \gamma V_\varphi(s') - V_\varphi(s)) \nabla_\varphi V_\varphi(s) \]
因此,TD 实际上是最小化奖励预测误差(RPE):
梯度蒙特卡罗值估计算法
算法步骤:
- 初始化参数 \(\varphi\) 为 0 或随机值;
- while 未收敛:
- 按策略 \(\pi\) 生成一个完整回合 \(\tau = (s_0, a_0, r_1, s_1, \ldots, s_T)\);
- 对每个状态 \(s_t\):
- 计算回报 \(R_t = \sum_k \gamma^k r_{t+k+1}\);
- 更新参数:\[\Delta \varphi = \eta (R_t - V_\varphi(s_t)) \nabla_\varphi V_\varphi(s_t) \]
该算法无偏(因使用真实回报),但方差较高。
半梯度时间差分值估计算法
算法步骤:
- 初始化参数 \(\varphi\);
- while 未收敛:
- 从初始状态 \(s_0\) 开始;
- 对于每一步:
- 按策略 \(\pi\) 选择动作;
- 执行动作,观察 \((r_{t+1}, s_{t+1})\);
- 更新参数:\[\Delta \varphi = \eta (r_{t+1} + \gamma V_\varphi(s_{t+1}) - V_\varphi(s_t)) \nabla_\varphi V_\varphi(s_t) \]
- 若 \(s_{t+1}\) 为终止状态:break
该方法方差较小,但由于 \(V_\varphi(s_{t+1})\) 初期估计误差大,因此存在显著偏差。
动作值函数逼近
同样可以用参数化函数 \(Q_\theta(s,a)\) 逼近 Q 值。
两种常见结构如下:
-
以 \((s,a)\) 的联合特征向量为输入,输出单个 Q 值;
-
仅以状态特征为输入,输出每个可能动作的 Q 值(适用于离散动作空间)。
在两种情况下,目标都是最小化真实 Q 值 \(Q^\pi(s,a)\) 与近似值 \(Q_\theta(s,a)\) 之间的均方误差,可用 SARSA 或 Q-learning 估计目标。
函数逼近的 Q-learning 算法
算法步骤:
- 初始化参数 \(\theta\);
- while True:
- 从初始状态 \(s_0\) 开始;
- 对于每一步:
- 按行为策略 \(b\)(如 \(\epsilon\)-greedy)选择动作 \(a_t\);
- 执行动作,观察 \((r_{t+1}, s_{t+1})\);
- 更新参数:\[\Delta \theta = \eta (r_{t+1} + \gamma \max_a Q_\theta(s_{t+1}, a) - Q_\theta(s_t, a_t)) \nabla_\theta Q_\theta(s_t, a_t) \]
- 贪婪改进策略:\[\pi(s_t, a) = \text{Greedy}(Q_\theta(s_t, a)) \]
- 若 \(s_{t+1}\) 为终止状态:break
基于策略的函数逼近(Policy-based Function Approximation)
在策略逼近中,目标是直接学习一个参数化策略 \(\pi_\theta(s,a)\),使其最大化期望回报。
定义目标函数为:
其中轨迹 \(\tau = (s_0, a_0, s_1, a_1, \ldots, s_T)\) 的概率由策略 \(\pi_\theta\) 决定。
学习的目标是让策略产生高回报的轨迹,同时避免低回报的轨迹。
该目标函数理论上正确,但计算上不可行(需对所有可能轨迹积分)。
