A. 灯若辰星
题面link
赛时
一眼看出\(F\)属于第一类斯特林数,但\(G\)死活找不出规律QAQ。
然后又没对\(F mod 2\)进行分讨,0pts遗憾离场。。。
正解
让我们分开求解
F
手搓几个样例可发现其中的递推关系
rt:
考虑以下序列

其对应的图
尝试将一个点\(7\)放入序列中:
发现有两种情况
- 其单独成为一个连通块
此时连通块的个数加一
rt:
![image]()
- 和其他的连通块连接
此时连通块的个数不变
且有六(n-1)种连接方式(即分别和1,2,3,4,5,6连)
可以自己手模一下(不画是因为画图太难用惹。。)
由此得出求\(F(n,m)\)的递推式
发现其显然是第一类斯特林数,但观察1e9的\(n,m\)数据范围,递推显然不可做。
于是,我们从mod 2性质入手,对\(n\)的奇偶性进行分讨。
发现:
设其以下转移方式生成的为\(F'(n,m)\);
当\(n\)是奇数时,\(F(n,m)\)从\(F(n−1,m−1)\)转移。
当\(n\)是偶数时,\(F(n,m)\)从\(F(n−1,m−1),F(n−1,m)\)转移
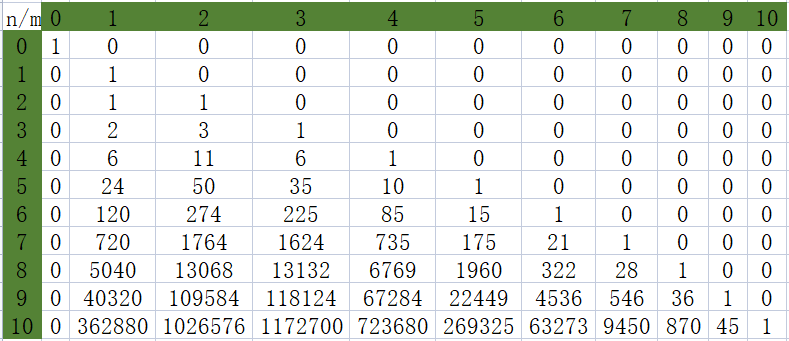
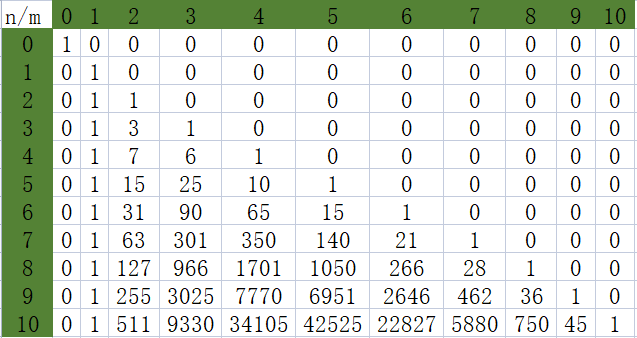
打表可得:
\(F(n,m)\)
\(F'(n,m)\)
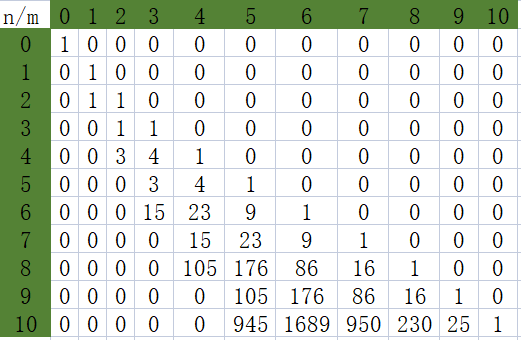
\(F(n,m)\mod2\)

\(F'(n,m)\mod2\)

其\(F(n,m)\mod2\)与\(F'(n,m)\mod2\)是相同的,即算出的答案是相同的。
观察发现\(F'(n,m)\)有以下几个取值:
好让我们先处理到这里,剩下的等会再说(因为我要去次饭啦)
G
手搓几个样例没发现其中的递推关系
赛后打开题解发现是第二类斯特林数
但那些奇奇怪怪的2的幂把鱼鱼撞晕惹(其实今天胯骨和后腰十分的痛但不是被它撞的,其实也不知为什么link)
所以只好去问了QEDQEDQED大蛇,豁然开朗!!再此%%%%%%%
让我们考虑以下两个图:
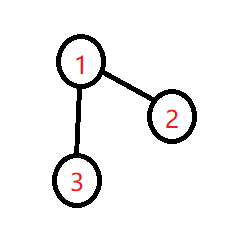
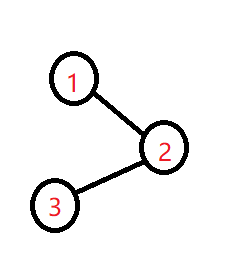
对于\(F\)来说,这两个是不同的连通块
但对于\(G\)中的\(val\)来说,它们是相同的
观察\(G\)的计算方式,发现若\(val\)有一个不同则\(G\)不同。(因为它的底数是2,由二进制的性质可得)
所以就可以将上图转化为一个集合\(\{1,2,3 \}\),若将一个元素\(4\)与其集合内的元素连接,只需将\(4\)加入这个集合。
所以有以下两个情况:
- 其单独成为一个集合
此时集合(连通块)的个数加一 - 加入其他的集合
此时集合的个数不变
且有连通块(m)种连接方式(即分别m个连通块连)
由此得出求\(G(n,m)\)的递推式
没发现其显然是第二类斯特林数,但观察1e9的\(n,m\)数据范围,递推当然不可做。
于是,我们又mod 2性质入手,对\(m\)的奇偶性进行分讨。
发现:
设其以下转移方式生成的为\(G'(n,m)\);
当\(m\)是奇数时,\(G(n,m)\)从\(G(n−1,m−1)\)转移。
当\(m\)是偶数时,\(G(n,m)\)从\(G(n−1,m−1),G(n−1,m)\)转移
打表可得:
\(G(n,m)\)
\(G'(n,m)\)
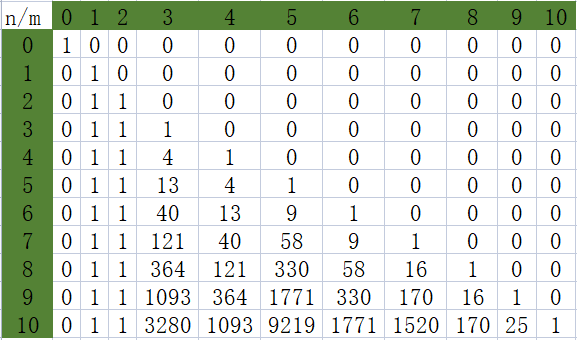
\(G(n,m)\mod2\)
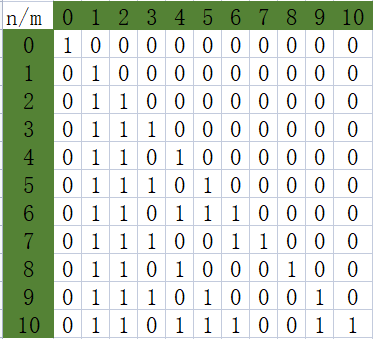
\(G'(n,m)\mod2\)

其\(G(n,m)\mod2\)与\(G'(n,m)\mod2\)是相同的,即算出的答案是相同的。
观察发现\(G'(n,m)\)有以下几个取值:
答案统计
发现组合数是无法计算辣么大的数的,让我们从\(\mod 2\)来考虑,提供以下两种方式。
- 使用Lucas定理
发现\(2\)是一个不大的质数,套用Lucas定理计算组合数
引用:Lucas 定理(from:Oi Wiki)
Lucas定理的代码实现
#include<iostream>
using namespace std;
int Q,n,m,op;
int C(int n,int m)
{if(m==0||m==n){return 1;}if(n==0){return 0; }return C(n%2,m%2)*C(n/2,m/2);
}
int F(int n,int m)
{return C((2*m-n)/2+n-m,n-m)%2;
}
int G(int n,int m)
{return C((m-1)/2+n-m,n-m)%2;
}
int main()
{freopen("light1.in","r",stdin);freopen("light.out","w",stdout); ios::sync_with_stdio(false);cin>>Q;while(Q--){cin>>op>>n>>m;if(n<m||(op==1&&2*m<n)) {cout<<0; }else if(m==0) {if(n==0){cout<<1;}else{cout<<0;}}else if(op==1){cout<<F(n,m);}else{cout<<G(n,m);}}return 0;
}
- 使用二进制集合关系求解
引理:\(\binom{n}{m}\mod 2=[m\subset n]\)
即\(n\) 在二进制下包含 \(m\) (\(m\)的二进制是\(n\)的二进制的子串)
证明:
根据Lucas定理,组合数 \(\binom{n}{m}\equiv \binom{\llcorner \frac{n}{2} \lrcorner}{\llcorner \frac{m}{2} \lrcorner} \times \binom{n \bmod 2}{m \bmod 2} \pmod{2}\)
于是,设\(n\)的二进制分解为\(n=\begin{matrix} \sum_{} a_i2^i \end{matrix}\),\(m\)的二进制分解为\(m=\begin{matrix} \sum_{} b_i2^i \end{matrix}\) (\(a_i,b_i \in\{0,1 \}\))
则\(\binom{n}{m}\equiv \begin{matrix} \prod _{} \binom{a_i}{b_i} \end{matrix} \pmod{2}\)
显然:\(\binom{0}{0}=1\) \(\binom{0}{1}=0\) \(\binom{1}{0}=1\) \(\binom{1}{1}=1\)
所以\(\binom{n}{m}\equiv 1 \pmod{2}\)当且仅当不能出现 \(a_i=0,b_i=1\)
于是即为 \(n\) 在二进制下包含 \(m\)。
二进制集合关系的代码实现
#include<iostream>
using namespace std;
int Q,n,m,op;
int F(int n,int m)
{if(((n-m)|((2*m-n)/2+n-m))==((2*m-n)/2+n-m)){return 1;}else{return 0;}
}
int G(int n,int m)
{if(((n-m)|((m-1)/2)+n-m)==((m-1)/2+n-m)){return 1;}else{return 0;}
}
int main()
{freopen("light.in","r",stdin);freopen("light.out","w",stdout); ios::sync_with_stdio(false);cin>>Q;while(Q--){cin>>op>>n>>m;if(n<m||(op==1&&2*m<n)) {cout<<0; }else if(m==0) {if(n==0){cout<<1;}else{cout<<0;}}else if(op==1){cout<<F(n,m);}else{cout<<G(n,m);}}return 0;
}