分块
我们以P3372 【模板】线段树 1 - 洛谷为模板讲一下
概览
首先,严格意义上将分块并不是一种数据结构,而是一种思路
顾名思义,就是把一个东西分成很多个块,一个块一个块遍历
所以分块就是一种优雅的暴力,只是把一个一个遍历变成了多个多个遍历
预处理操作
首先,要进行分块
块太多或者块太少都会影响时间,所以这里每个块有 \(\sqrt n\) 个元素
然后并不是每一个数都是完全平方数,所以最后多出来的一小部分单独成块
那么,我们需要记录一下每一个块的首尾节点
可以发现,右端点实际上就是 \(i\sqrt n\),那么左端点就可以用上一个右端点加一得到
同时,最后一个要特殊处理,因为我们只有 \(n\) 个元素
int len=sqrt(n);//每一块的数量
int num=n/len;//块数
if(n%len!=0){num++;//不为完全平方数特殊判断
}
for(int i=1;i<=num;i++){//总共num块L[i]=(i-1)*len+1;//左=上一个右+1R[i]=i*len;
}
R[num]=n;//最后一块特殊处理
然后,记录每一块的初始值和每一个点所在的块
for(int i=1;i<=num;i++){for(int j=L[i];j<=R[i];j++){pos[j]=i;//j号点在第i块中val[i]+=a[j];//第i块的初始答案}}
修改操作
我们的分块可以这样理解:
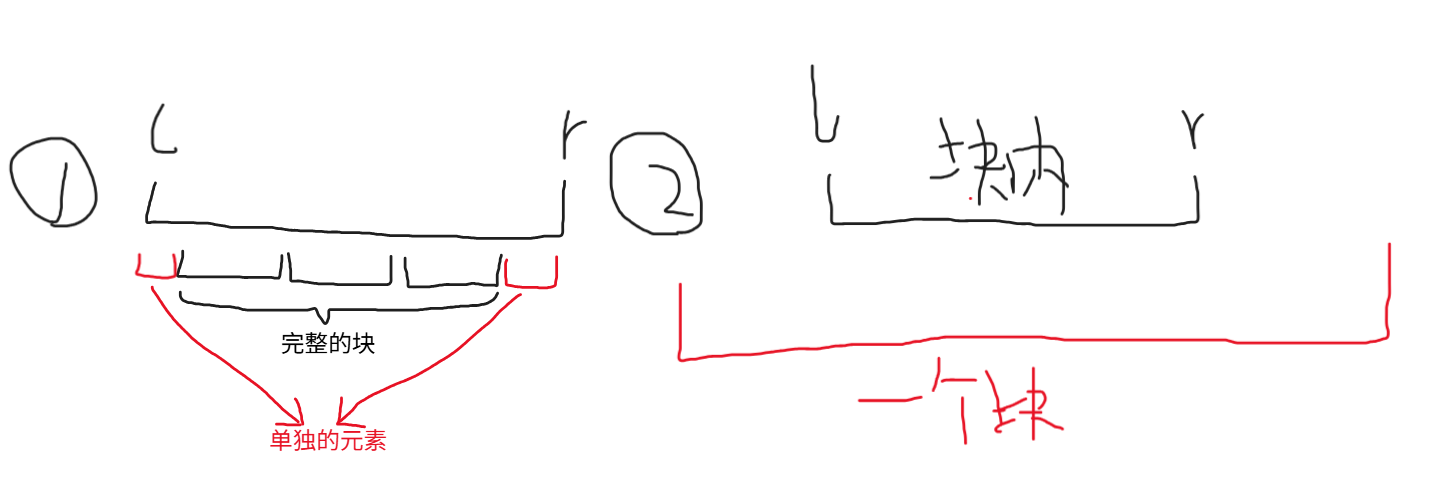
对于情况1
我们先枚举两个单独的区间,再给中间的完整区间打上lazy标记
对于情况2
我们直接枚举l到r,暴力修改
所以分块的代码不难
void update(int x,int y,int k){int b1=pos[x],b2=pos[y];//获取两个点所在的块if(b1==b2){//情况2(同一块)for(int i=x;i<=y;i++){a[i]+=k;//暴力修改val[b1]+=k;//别忘了加块内答案}}else{//情况2(不同块)for(int i=b1+1;i<b2;i++){//枚举中间的完整块lazy[i]+=k;//打上懒标记val[i]+=(R[i]-L[i]+1)*k;//累加区间答案}for(int i=x;i<=R[b1];i++){//左区间枚举a[i]+=k;//暴力修改val[b1]+=k;//加块内答案}for(int i=L[b2];i<=y;i++){//右区间枚举a[i]+=k;val[b2]+=k;}}
}
查询
同理,思路不展示了,细节见代码
int query(int x,int y){int b1=pos[x],b2=pos[y],ans=0;if(b1==b2){for(int i=x;i<=y;i++){ans+=a[i]+lazy[b1];//记得加上懒标记}}else{for(int i=b1+1;i<b2;i++){ans+=val[i];}for(int i=x;i<=R[b1];i++){ans+=a[i]+lazy[b1];//同上}for(int i=L[b2];i<=y;i++){ans+=a[i]+lazy[b2];//同上}}return ans;
}
总结
分块是一种优化暴力思路,可在 \(O(\sqrt n)\) 的时间内完成区间查询和区间修改操作,在\(O(n)\)的时间复杂度内完成预处理操作,时间比线段树和树状数组略差,但比线段树和树状数组更为灵活
那么自行整合完成P3372 【模板】线段树 1 - 洛谷
P4145 上帝造题的七分钟 2 / 花神游历各国 - 洛谷
请先自行思考
思路如下
首先,开平方操作肯定不能区间做
但是,我们可以发现,开平方最后只能到1这个数,所以我们在区间修改的时候特判区间长度是否和答案一样(全为1),如果是就跳过,剩下的就一个一个暴力修改
void init(){int len=sqrt(n);int num=n/len;if(n%len!=0){num++;}for(int i=1;i<=num;i++){L[i]=(i-1)*len+1;R[i]=i*len;}R[num]=n;for(int i=1;i<=num;i++){for(int j=L[i];j<=R[i];j++){pos[j]=i;val[i]+=a[j];}}
}
void update(int x,int y){int b1=pos[x],b2=pos[y];if(b1==b2){for(int i=x;i<=y;i++){val[b1]-=a[i];a[i]=sqrt(a[i]);val[b1]+=a[i];}}else{for(int i=b1+1;i<b2;i++){if(val[i]==(R[i]-L[i]+1)){continue;}for(int j=L[i];j<=R[i];j++){val[i]-=a[j];a[j]=sqrt(a[j]);val[i]+=a[j];}}for(int i=x;i<=R[b1];i++){val[b1]-=a[i];a[i]=sqrt(a[i]);val[b1]+=a[i];}for(int i=L[b2];i<=y;i++){val[b2]-=a[i];a[i]=sqrt(a[i]);val[b2]+=a[i];}}
}
int query(int x,int y){int b1=pos[x],b2=pos[y],ans=0;if(b1==b2){for(int i=x;i<=y;i++){ans+=a[i];}}else{for(int i=b1+1;i<b2;i++){ans+=val[i];}for(int i=x;i<=R[b1];i++){ans+=a[i];}for(int i=L[b2];i<=y;i++){ans+=a[i];}}return ans;
}
