深度学习(Deep Learning)
深度强化学习(Deep RL)使用深度神经网络作为函数逼近器,从而能够学习状态–动作对的复杂表示。本节对深度学习进行简要概述,更多细节可参考 @Goodfellow2016。
前馈神经网络(Feedforward Neural Networks)
一个深度神经网络(DNN)或多层感知机(MLP)由输入层 \(\mathbf{x}\)、一个或多个隐藏层 \(\mathbf{h_1}, \mathbf{h_2}, \ldots, \mathbf{h_n}\),以及输出层 \(\mathbf{y}\) 组成。
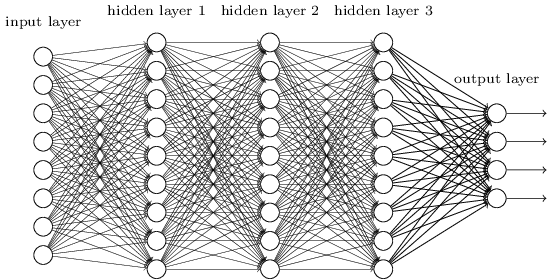
每一层(称为全连接层,FC层)将上一层的输出向量 \(\mathbf{h_{k-1}}\) 通过线性变换和非线性激活函数转换为新的表示:
其中 \(W_k\) 为权重矩阵,\(\mathbf{b_k}\) 为偏置项,\(f\) 为激活函数。
现代网络常用的激活函数是 ReLU(Rectified Linear Unit):\(f(x)=\max(0, x)\),也可使用其变体。
学习的目标是找到参数集 \(\theta\)(包含所有权重和偏置),使定义在训练集 \(\mathcal{D}\) 上的损失函数最小化。
-
回归问题中最小化均方误差(MSE):
\[\mathcal{L}(\theta) = \mathbb{E}_{\mathbf{x}, \mathbf{t} \in \mathcal{D}} [||\mathbf{t} - \mathbf{y}||^2] \]其中 \(\mathbf{x}\) 为输入,\(\mathbf{t}\) 为真实输出,\(\mathbf{y}\) 为预测值。
-
分类问题中最小化交叉熵(或负对数似然):
\[\mathcal{L}(\theta) = - \mathbb{E}_{\mathbf{x}, \mathbf{t} \in \mathcal{D}} [\sum_i t_i \log y_i] \]分类任务中输出层通常采用 softmax 激活,与交叉熵函数配合良好。
定义损失函数后,通过梯度下降(Gradient Descent)优化参数:
其中 \(\eta\) 为学习率。若梯度为正,说明增加该参数会使损失变大,应减少它;反之则增加。
梯度的计算由反向传播(Backpropagation)算法实现,即链式法则在神经网络中的应用:
每一层在反向传播中对梯度都有贡献。
对于 @eq-fullyconnected 所示的全连接层:
ReLU 的导数简单易算:
现代框架(TensorFlow、PyTorch等)会自动计算这些梯度。
接下来需要选择一个优化器(Optimizer)来更新参数。
常用优化器包括:
- SGD(随机梯度下降)
- SGD + 动量(Momentum / Nesterov)
- Adagrad
- Adadelta
- RMSprop
- Adam
经验上,SGD + Nesterov 动量效果较好但需调参;Adam一般“开箱即用”,因此在深度强化学习中更常使用 Adam。
为防止过拟合,还可引入正则化机制:L1/L2 正则化、Dropout、Batch Normalization 等。
卷积神经网络(Convolutional Neural Networks, CNN)
卷积神经网络是为处理高维输入(如图像)而设计的 DNN 变体。
其核心思想是:隐藏层中的神经元在输入空间上共享权重,从而捕捉局部特征(如边缘)。
卷积层(Convolutional Layer)使用若干小矩阵(如 3×3 或 5×5)作为卷积核,在输入图像上滑动计算,生成特征图(Feature Maps)。
如果输入为 \(N \times M \times 3\) 彩色图像,则卷积层输出为 \(N \times M \times F\) 的张量,\(F\) 为提取的特征数。
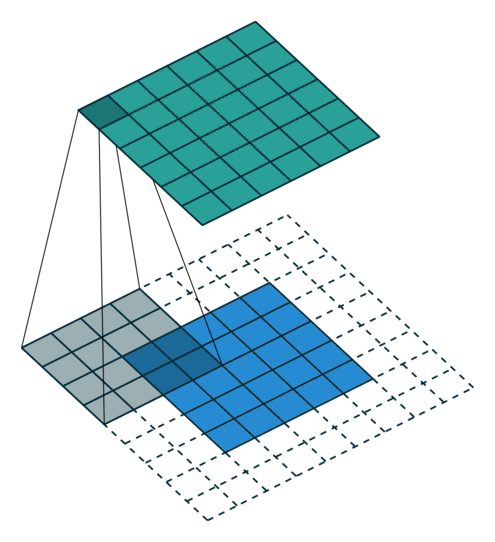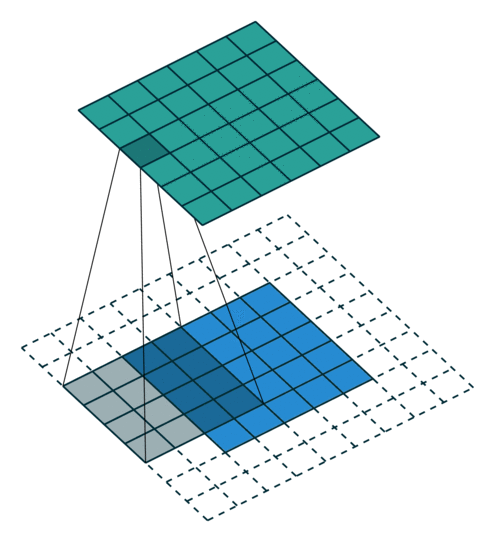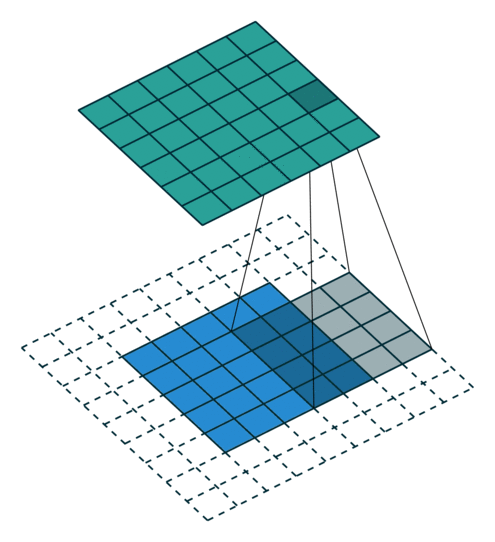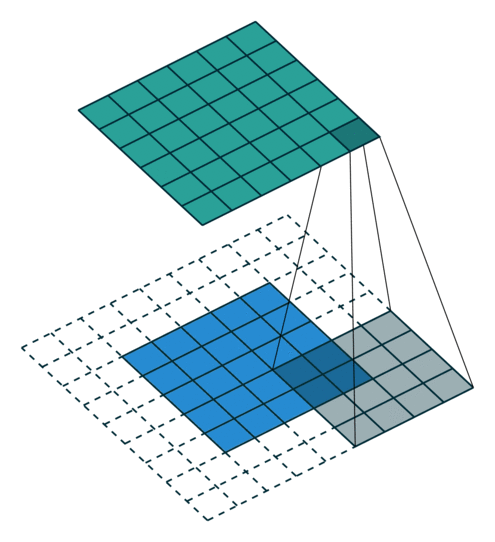
卷积层保持空间尺寸,而最大池化层(Max-Pooling Layer)用于降低空间分辨率并增强平移不变性:
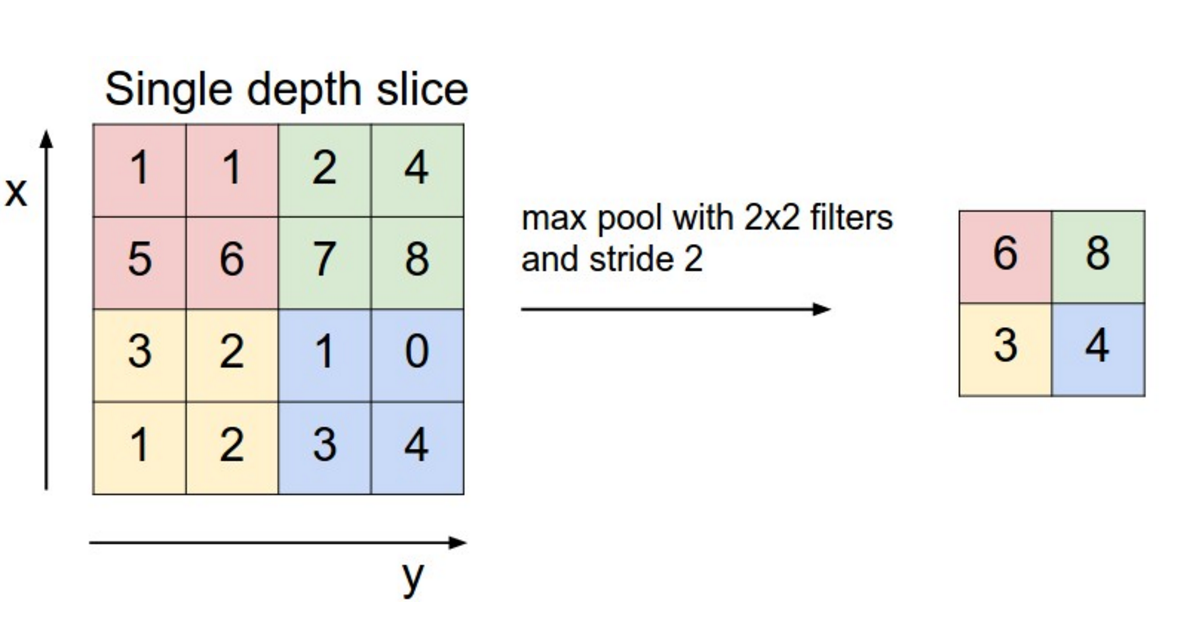
每个特征图被划分为 2×2 区块,仅保留每块中的最大激活值,从而使尺寸减半。
典型的 CNN 结构由若干卷积层和池化层交替组成,最后连接全连接层与 softmax 输出层。
下图展示了 2012 年 ImageNet 冠军模型 AlexNet 的结构:

虽然自 2012 年以来已有许多改进(如 ResNet),但基本思想相同:
卷积层提取特征,池化层下采样,最后将小尺寸特征映射展平送入全连接层。
在深度强化学习中,通常不使用池化层。
因为位置信息至关重要(例如球的位置、人物的朝向等),去掉池化层可保留空间细节。
这会增加网络参数量与所需样本量,也是 CNN 在深度强化学习中最大的限制。
循环神经网络(Recurrent Neural Networks, RNN)
前馈网络只能处理静态输入 \(\mathbf{x}\),输出 \(\mathbf{y}\),无法捕捉时间依赖。
在处理序列任务(如视频分析)时,这会导致低效。
循环神经网络(RNN)通过引入时间递归解决此问题:当前输出依赖于当前输入和上一步输出。
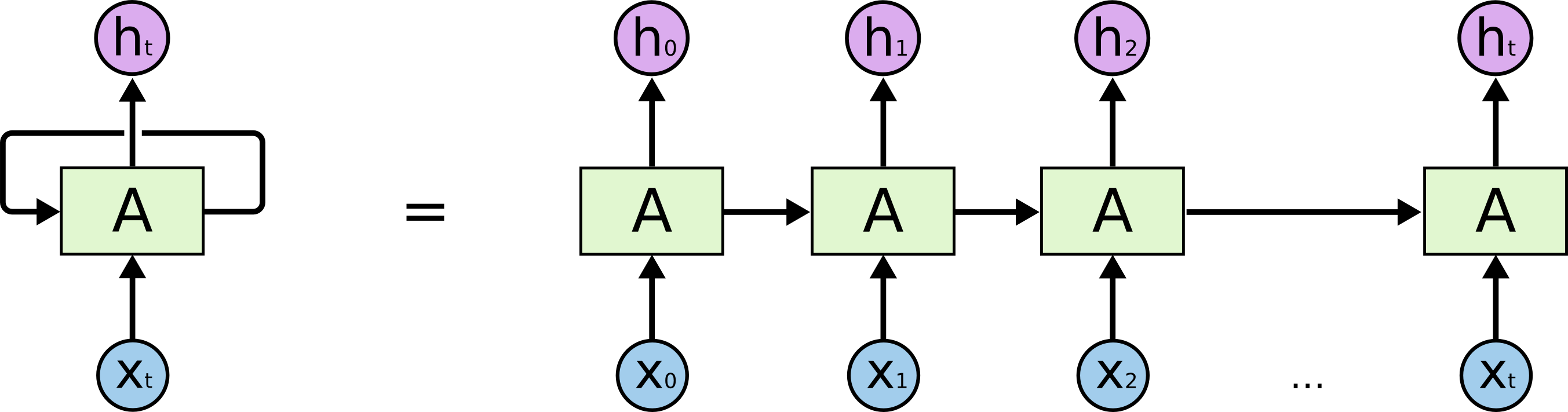
RNN 通过“时间反向传播”(BPTT)更新参数。
但由于梯度在时间步间多次相乘,若 \(|W_h|<1\),梯度会消失;若 \(|W_h|>1\),梯度会爆炸。
为解决此问题,引入了长短期记忆网络(LSTM) [@Hochreiter1997]。
LSTM 在标准 RNN 的基础上加入了一个“记忆单元” \(\mathbf{C}_t\) 及三个门控:输入门、遗忘门和输出门。
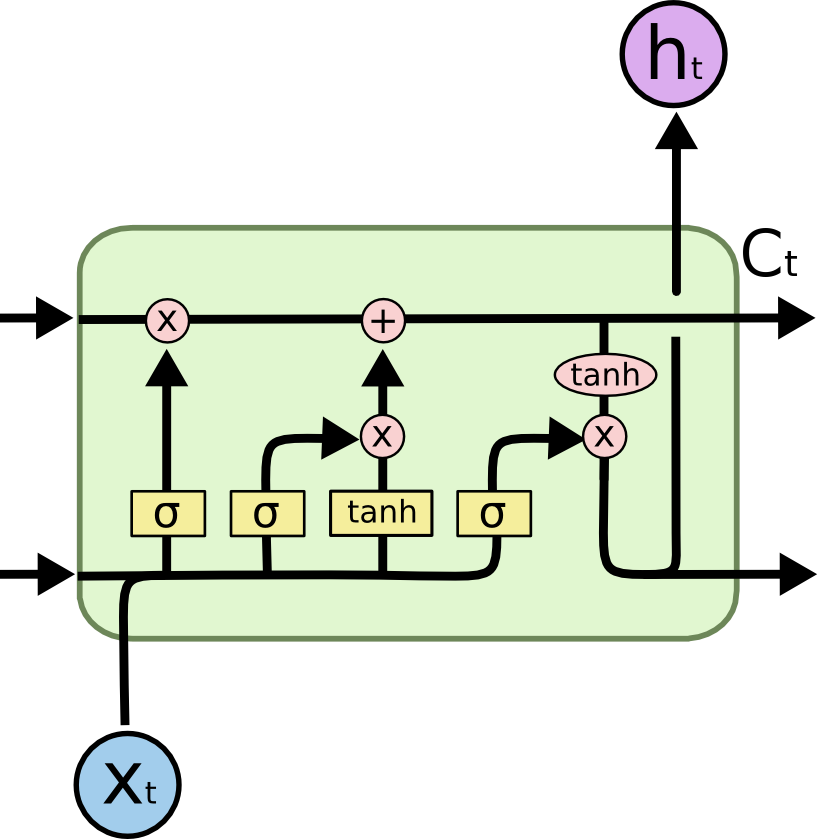
-
候选状态:
\[\tilde{\mathbf{C}_t} = f(W_x \mathbf{x}_t + W_h \mathbf{h}_{t-1} + \mathbf{b}) \] -
输入门:
\[\mathbf{i}_t = \sigma(W^i_x \mathbf{x}_t + W^i_h \mathbf{h}_{t-1} + \mathbf{b}^i) \] -
遗忘门:
\[\mathbf{f}_t = \sigma(W^f_x \mathbf{x}_t + W^f_h \mathbf{h}_{t-1} + \mathbf{b}^f) \] -
状态更新:
\[\mathbf{C}_t = \mathbf{i}_t \odot \tilde{\mathbf{C}_t} + \mathbf{f}_t \odot \mathbf{C}_{t-1} \] -
输出门与最终输出:
\[\mathbf{o}_t = \sigma(W^o_x \mathbf{x}_t + W^o_h \mathbf{h}_{t-1} + \mathbf{b}^o) \]\[\mathbf{h}_t = \mathbf{o}_t \odot \tanh(\mathbf{C}_t) \]
LSTM 可避免梯度消失问题,并能在长时间跨度上保留关键信息。
其变体包括 GRU(门控循环单元)[@Cho2014] 和 Peephole LSTM [@Gers2001]。
在深度强化学习中,RNN 尤其适用于部分可观测马尔可夫决策过程(POMDP),例如:单帧图像中不包含速度信息,LSTM 可在时间上整合多帧输入,从而隐式地表示速度等状态信息。
Transformer
即将添加
扩散模型(Diffusion Models)
即将添加
