3.5 自然梯度（Natural Gradients）

自然梯度（Natural Gradients）

---

学习稳定性

此前介绍的深度强化学习方法均使用随机梯度下降（SGD）或其变体（RMSProp、Adam 等）来训练神经网络函数逼近器。
其基本思想是：沿损失函数梯度的反方向（或策略梯度的正方向）按比例调整参数 \(\theta\)：

\[\Delta \theta = - \eta \, \nabla_\theta \mathcal{L}(\theta) \]

SGD 也被称为最速下降法（steepest descent）：
目标是在参数变化尽可能小的前提下，使损失函数下降得最快。
在监督学习中，这种方式效果良好，但学习率的选择十分关键：

• 学习率过大 → 不稳定；
• 学习率过小 → 收敛缓慢。

在强化学习中，情况更复杂：问题是非平稳的（non-stationary）。
例如在 Q-learning 中，目标 \(r + \gamma \max_{a'} Q_\theta(s',a')\) 会随着 \(\theta\) 不断变化。
若目标变化过快，模型将无法稳定收敛。
DQN 使用目标网络（target network）来缓解该问题，但会引入偏差与高样本复杂度。

在 on-policy 方法中无法使用目标网络，尤其在 Actor–Critic 框架中：
评论者必须从当前演员生成的最新样本中学习。
若策略更新过快，评论者提供的 Q 值将代表完全不同的策略，导致梯度严重偏差。

一种直观的解决方法是：降低演员的学习率，但这只会让学习更慢。

因此，更合理的思路是——

寻找能让参数变化尽可能大、但策略变化尽可能小的方向。

若每次更新后策略变化很小，便能更好地复用过往经验，减少样本浪费。
这正是自然梯度（Natural Gradient）的核心思想。

最早由 @Amari1998 提出，用于在概率分布空间上进行高效优化。
@Kakade2001 将其引入策略梯度理论；
@Peters2008 进一步提出自然演员–评论家（Natural Actor–Critic, NAC）算法。
后续 @Schulman2015 与 @Schulman2017 分别发展出 TRPO 与 PPO，成为当前强化学习中最稳定且高效的策略优化方法。

---

自然梯度的原理

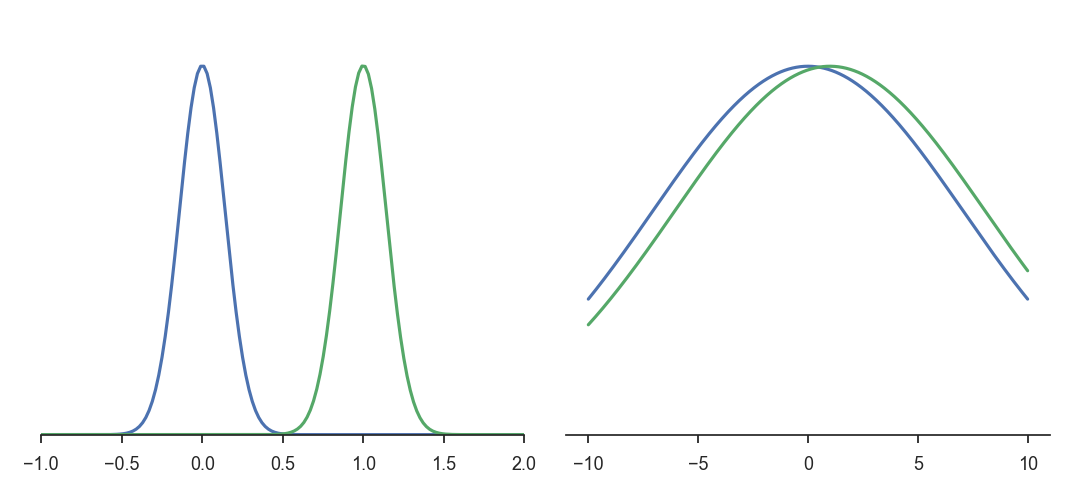
考虑两对高斯分布：

• 左侧：\(\mathcal{N}(0,0.2)\) 与 \(\mathcal{N}(1,0.2)\)；
• 右侧：\(\mathcal{N}(0,10)\) 与 \(\mathcal{N}(1,10)\)。

两组分布在参数空间中的欧几里得距离相同，但右侧分布显然更接近。
这说明：参数空间的欧几里得距离无法正确刻画概率分布的相似性。

衡量分布差异的常用指标是 Kullback–Leibler (KL) 散度：

\[D_{KL}(p||q) = \mathbb{E}_{x \sim p}[\log \frac{p(x)}{q(x)}] \]

当 \(p=q\) 时取最小值 0。
机器学习的监督学习目标实际上也可理解为最小化 KL 散度：
希望模型输出分布 \(q(x)\) 与真实标签分布 \(p(x)\) 一致。

由于 KL 散度不对称，常使用对称形式——Jensen–Shannon (JS) 散度：

\[D_{JS}(p||q) = \frac{D_{KL}(p||q) + D_{KL}(q||p)}{2} \]

---

Riemann 度量与 Fisher 信息矩阵

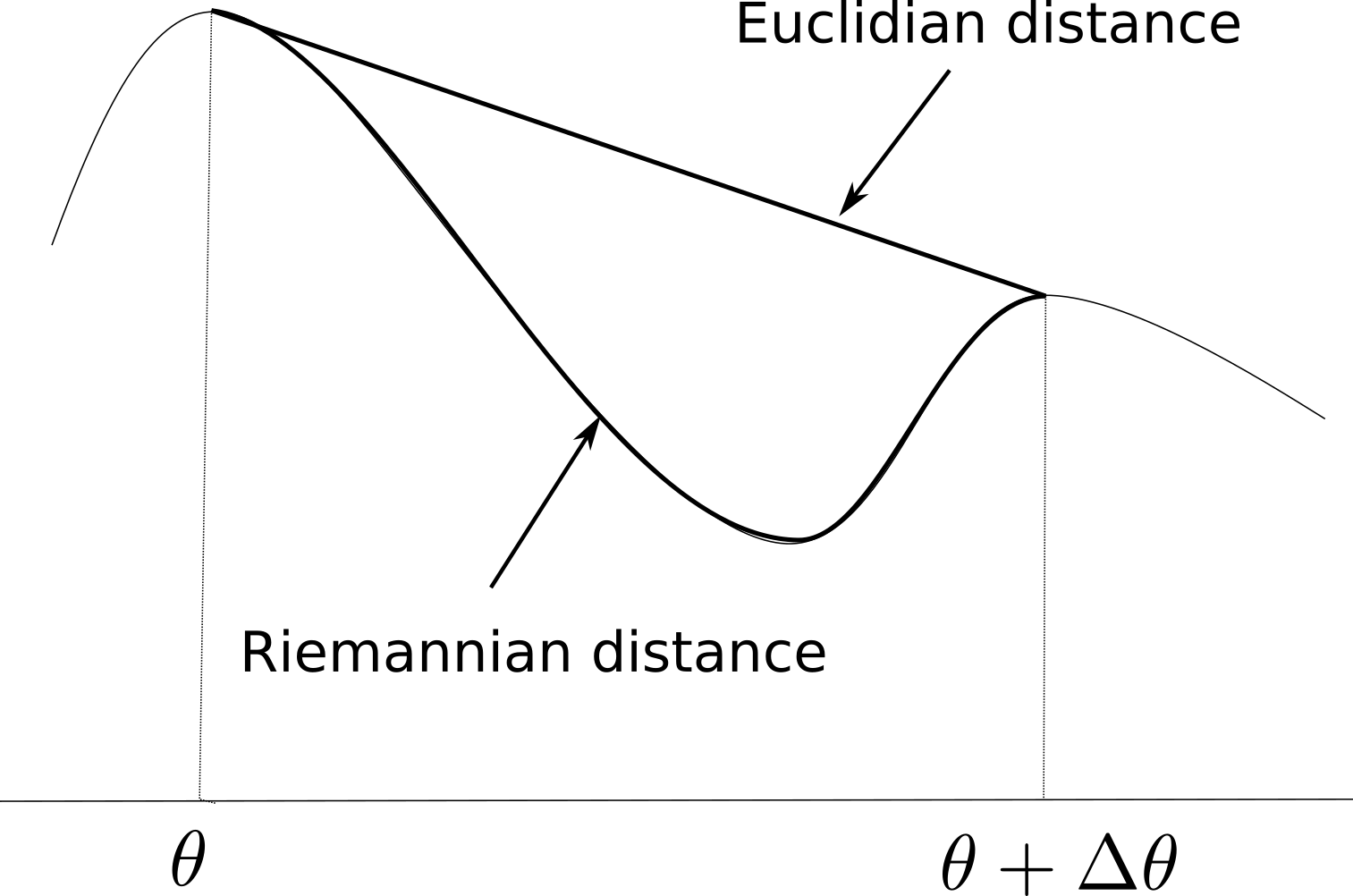
设有参数化分布 \(p(x;\theta)\)。
若参数发生微小变化 \(\Delta \theta\)，则对应分布 \(p(x;\theta + \Delta \theta)\)。
在参数空间中，欧几里得距离无法反映流形结构。
我们引入 Riemann 度量（Riemannian Metric），定义为：

\[||\Delta \theta||^2 = \langle \Delta \theta, F(\theta) \Delta \theta \rangle \]

其中 \(F(\theta)\) 称为度量张量（metric tensor）。
当使用 KL 散度定义距离时，\(F(\theta)\) 即为Fisher 信息矩阵（FIM）：

\[F(\theta) = \mathbb{E}_{x \sim p(x;\theta)}[\nabla \log p(x;\theta)(\nabla \log p(x;\theta))^T] \]

它表示流形在 \(\theta\) 附近的局部曲率。

局部二阶展开可得：

\[D_{JS}(p(x;\theta) || p(x;\theta+\Delta\theta)) \approx \Delta\theta^T F(\theta)\Delta\theta \]

因此最小化 KL 散度等价于考虑 Fisher 矩阵加权下的“真实”梯度方向。

---

自然梯度定义

自然梯度通过修正普通梯度的方向与尺度，使其在统计流形上以“自然距离”前进：

\[\tilde{\nabla_\theta} L(\theta) = F(\theta)^{-1} \nabla_\theta L(\theta) \]

更新规则为：

\[\Delta \theta = -\eta \, \tilde{\nabla_\theta} L(\theta) \]

当 \(F(\theta)\) 为单位矩阵时，自然梯度退化为普通梯度。
与传统 SGD 相比：

• 平坦区域（曲率小）中：步长增大，加快收敛；
• 陡峭区域（曲率大）中：步长减小，避免震荡；
• 收敛更稳定、学习率敏感性更低。

其主要缺点是：需计算并求逆 Fisher 信息矩阵（维度为参数数目平方）。
常用近似方法包括：

• 共轭梯度法（Conjugate Gradient）；
• Kronecker 分解近似（K-FAC）。

---

自然策略梯度（Natural Policy Gradient）与自然演员–评论家（NAC）

@Kakade2001 将自然梯度原理应用于策略梯度定理：

\[\nabla_\theta J(\theta) = \mathbb{E}_{s \sim \rho_\theta, a \sim \pi_\theta}[\nabla_\theta \log \pi_\theta(s,a) Q^{\pi_\theta}(s,a)] \]

其 Fisher 信息矩阵为：

\[F(\theta) = \mathbb{E}_{s \sim \rho_\theta, a \sim \pi_\theta}[\nabla \log \pi_\theta(s,a)(\nabla \log \pi_\theta(s,a))^T] \]

自然策略梯度为：

\[\tilde{\nabla_\theta} J(\theta) = F(\theta)^{-1} \nabla_\theta J(\theta) \]

可理解为：在保持策略变化最小的情况下，使期望回报提升最大。

@Kakade2001 证明：

• 可将 \(Q^{\pi_\theta}\) 替换为任意满足兼容条件的近似 \(Q_\varphi\)；
• 自然梯度保证策略单调改进（每次更新后策略性能不下降）。

@Peters2008 提出 自然演员–评论家（Natural Actor–Critic, NAC），
在此基础上进一步推导了低方差基线与采样版本的 Fisher 矩阵近似，
并在机器人学习（如棒球挥杆控制）中验证其高效性。

---

进一步阅读

• http://andymiller.github.io/2016/10/02/natural_gradient_bbvi.html
• https://hips.seas.harvard.edu/blog/2013/01/25/the-natural-gradient/
• http://kvfrans.com/what-is-the-natural-gradient-and-where-does-it-appear-in-trust-region-policy-optimization
• https://wiseodd.github.io/techblog/2018/03/14/natural-gradient/
• John Schulman（OpenAI）讲座视频：https://www.youtube.com/watch?v=xvRrgxcpaHY
• 共轭梯度与 Hessian-free 优化教程：http://andrew.gibiansky.com/blog/machine-learning/hessian-free-optimization/
• K-FAC 方法综述：https://syncedreview.com/2017/03/25/optimizing-neural-networks-using-structured-probabilistic-models/
• 共轭梯度法入门：https://www.cs.cmu.edu/~quake-papers/painless-conjugate-gradient.pdf

注： 自然梯度也可用于 DQN 网络训练，可显著提升学习效率与稳定性 [@Knight2018]。