介绍
如题,这是一种适用于正整数值域的平衡树。其主要特点如下:
-
不带旋
-
常数小
-
实现简单,好理解
与此同时,该算法具有以下局限性:
-
只适用于正整数值域
-
时间复杂度依赖于值域大小
-
似乎只能解决传统平衡树问题
目前暂不清楚 OI 界是否有相同(或类似)的算法。
基本思想
假设我们将 \([1, 2^{31} - 1]\) 中的所有数都插入同一棵平衡树内,那么这棵平衡树的理想状态应该如下:
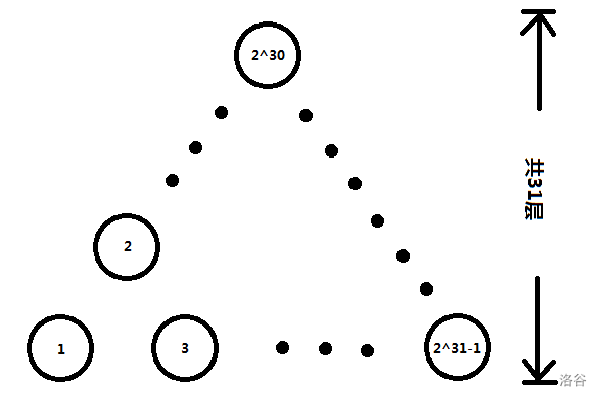
我们将上面这棵树称为值域 \([1, 2^{31} - 1]\) 内的理想平衡树。
一棵值域 \(V\) 内的理想平衡树,其树高为 \(\lceil \log V \rceil\)。
对应地,在值域 \(V\) 内,该算法构建的平衡树具有以下性质:
-
任意节点的父亲都为其在值域 \(V\) 内的理想平衡树内的祖先。
-
任意节点的左 / 右儿子均位于其在值域 \(V\) 内的理想平衡树内的左 / 右子树内。
可以看出具有这两条性质的平衡树的树高不超过 \(\lceil \log V \rceil\)。
具体内容
显然我们不能真的把值域里的所有数都存起来,所以我们需要动态开点。
节点结构
struct Node {ll l, r, val, cnt, siz;
};
\(l, r\):该节点的左 / 右儿子。
\(val\):该节点对应的值。
\(siz\):以该节点为根的子树的大小。
\(cnt\):该节点的大小。
你会发现这个结构跟普通 BST(二叉搜索树)没什么区别。
插入
从根节点开始递归,每遍历到一个节点,使该节点的 \(siz\) 加 \(1\)。
设插入的值为 \(x\),当前节点的编号为 \(i\):
- \(x = val_i\)
直接让 \(cnt_i\) 加 \(1\)。
- \(x < val_i\),且节点 \(i\) 不存在左儿子
直接在 \(i\) 的左儿子处插入一个值为 \(x\) 的节点。
- \(x < val_i\),且节点 \(i\) 存在左儿子
设 \(v\) 为 \(i\) 的左儿子的值,\(g\) 为 \(x\) 和 \(v\) 在理想线段树上对应节点的 \(\text{lca}\) 值。
若 \(g = v\),说明 \(x\) 应该在 \(v\) 对应节点的子树内。在 \(v\) 对应节点的子树内递归即可。
若 \(g = x\),说明 \(v\) 应该在 \(x\) 对应节点的子树内。将 \(i\) 的左儿子设为 \(v\),将 \(v\) 对应节点的左 / 右儿子设为 \(x\)(视 \(v, x\) 大小而定),并调整对应节点的 \(siz\)。
否则,\(x\) 和 \(v\) 都应该在 \(g\) 对应节点的子树内。
我们可以考虑在 \(i\) 的左子树内插入一个“虚拟节点”:该节点的值为 \(g\),但是该节点的 \(cnt\) 值为 \(0\),表示当前平衡树内不存在 \(g\) 这个数,这个节点是为了结构需要而设立的。
接下来将 \(x, v\) 分别设为这个虚拟节点的左 / 右儿子即可。可以证明 \(x, v\) 一个比 \(g\) 大,一个比 \(g\) 小。
当然上面的分类讨论还是太复杂了。我们可以将上面的所有操作简化为下面两步:
若 \(g \neq v\),则建立虚拟节点,将 \(i\) 的左儿子设为该虚拟节点,将 \(v\) 对应节点设为虚拟节点的儿子。
将 \(x\) 放在 \(i\) 的左子树内递归。
- \(x > val_i\)
同上。
时间复杂度 \(O(\log V)\)。
void add(Node &rt, ll x) {rt.siz++;if(x == rt.val) {rt.cnt++;return;}ll &l = (x < rt.val ? rt.l : rt.r);ll v, g;if(!l) {l = ++idx;tr[idx] = {0, 0, x, 1, 1};return;}v = tr[l].val, g = lca(v, x);if(g != v) {tr[++idx] = {(v < g) * l, (v > g) * l, g, 0, tr[l].siz};l = idx;}add(tr[l], x);
}
这样,该平衡树的插入操作就完成了。但我们还有一个非常重要的东西没讲——
如何求两个节点在理想线段树上对应节点的 \(\text{lca}\) 值
观察理想平衡树的结构,我们可以发现三个重要性质:
-
同一层节点的值的 \(\text{lowbit}\) 相等
-
一个节点的父亲的值为该节点的值加上 / 减去其 \(\text{lowbit}\)。
-
一个节点的父亲的 \(\text{lowbit}\) 为该节点的 \(\text{lowbit}\) 乘 \(2\)。
其中,上述性质中的 \(\text{lowbit}\) 与树状数组中的 \(\text{lowbit}\) 定义相同。
根据上述性质,我们可以得到下列结论:
设理想平衡树中某个节点的值为 \(x\) ,则其父亲的值为 \((x \oplus \text{lowbit}(x)) | (\text{lowbit}(x) << 1)\)
接下来我们记 \((x \oplus \text{lowbit}(x)) | (\text{lowbit}(x) << 1)\) 为 \(fa(x)\) 。
与此同时,我们得到了一个简单的求 \(u, v\) 在理想平衡树中的 \(\text{lca}\) 值的方法(假定 \(\text{lowbit}(u) \leq \text{lowbit}(v)\)):
-
若 \(\text{lowbit}(u) < \text{lowbit}(v)\),则 \(u := fa(u)\)。
-
若 \(\text{lowbit}(u) < \text{lowbit}(v)\) 且 \(u \neq v\),则 \(u := fa(u)\), \(v := fa(v)\)。
-
否则,\(u\) 即为我们所求的 \(\text{lca}\) 值。
由于树高为 \(\lceil \log V \rceil\),因此该方法的时间复杂度为 \(O(\log V)\)。
也许还有更优秀的方法,但 \(O(\log V)\) 的时间复杂度够用了。
#define lbt(x) (x & -x)
#define fa(x) ((x ^ lbt(x)) | (lbt(x) << 1))ll lca(ll x, ll y) {if(lbt(x) < lbt(y)) {swap(x, y);}while(lbt(y) < lbt(x)) {y = fa(y);}while(x != y) {x = fa(x), y = fa(y);}return x;
}
删除
暴力删除即可。
如果一个节点的 \(cnt\) 被减到 \(0\) 了,我们把它当做虚拟节点即可。
void del(Node &rt, ll x) {rt.siz--;if(x == rt.val) {rt.cnt--;return;}if(x < rt.val) {del(tr[rt.l], x);} else {del(tr[rt.r], x);}
}
求 \(x\) 排名 / 排名为 \(x\) 的数
同 BST,这里不再赘述。
ll rk(Node &rt, ll x) {if(x < rt.val) {return rt.l ? rk(tr[rt.l], x) : 0;} else if(x == rt.val) {return tr[rt.l].siz;} else {return tr[rt.l].siz + rt.cnt + (rt.r ? rk(tr[rt.r], x) : 0);}
}ll kth(Node &rt, ll x) {if(x <= tr[rt.l].siz) {return kth(tr[rt.l], x);} else if(x <= tr[rt.l].siz + rt.cnt) {return rt.val;} else {return kth(tr[rt.r], x - tr[rt.l].siz - rt.cnt);}
}
来做点板子
P3369 【模板】普通平衡树
注意到值域为 \([-10^7, 10^7]\),所以我们需要将值域整体右移。
需要在一开始插入一个虚拟根节点。要求该节点的值为 \(2^k\),可以设为 \(2^{30}\)(但对于这题可以不用这么大)。
#include <bits/stdc++.h>
#define lbt(x) (x & -x)
#define fa(x) ((x ^ lbt(x)) | (lbt(x) << 1))
using namespace std;
typedef long long ll;
constexpr ll N = 2e5 + 10;
struct Node {ll l, r, val, cnt, siz;
};
ll n, m, op, k, lst = 0, ans = 0, idx = 1;
array<Node, N> tr;ll lca(ll x, ll y) {if(lbt(x) < lbt(y)) {swap(x, y);}while(lbt(y) < lbt(x)) {y = fa(y);}while(x != y) {x = fa(x), y = fa(y);}return x;
}void add(Node &rt, ll x) {rt.siz++;if(x == rt.val) {rt.cnt++;return;}ll &l = (x < rt.val ? rt.l : rt.r);ll v, g;if(!l) {l = ++idx;tr[idx] = {0, 0, x, 1, 1};return;}v = tr[l].val, g = lca(v, x);if(g != v) {tr[++idx] = {(v < g) * l, (v > g) * l, g, 0, tr[l].siz};l = idx;}add(tr[l], x);
}void del(Node &rt, ll x) {rt.siz--;if(x == rt.val) {rt.cnt--;return;}if(x < rt.val) {del(tr[rt.l], x);} else {del(tr[rt.r], x);}
}ll rk(Node &rt, ll x) {if(x < rt.val) {return rt.l ? rk(tr[rt.l], x) : 0;} else if(x == rt.val) {return tr[rt.l].siz;} else {return tr[rt.l].siz + rt.cnt + (rt.r ? rk(tr[rt.r], x) : 0);}
}ll kth(Node &rt, ll x) {if(x <= tr[rt.l].siz) {return kth(tr[rt.l], x);} else if(x <= tr[rt.l].siz + rt.cnt) {return rt.val;} else {return kth(tr[rt.r], x - tr[rt.l].siz - rt.cnt);}
}int main() {cin.tie(nullptr)->sync_with_stdio(false);tr[1] = {0, 0, (1 << 30), 0, 0};cin >> m;while(m--) {cin >> op >> k;switch(op) {case 1:add(tr[1], k + (ll)1e7 + 1);break;case 2:del(tr[1], k + (ll)1e7 + 1);break;case 3:lst = rk(tr[1], k + (ll)1e7 + 1) + 1;break;case 4:lst = kth(tr[1], k) - (ll)1e7 - 1;break;case 5:lst = kth(tr[1], rk(tr[1], k + (ll)1e7 + 1)) - (ll)1e7 - 1;break;case 6:lst = kth(tr[1], rk(tr[1], k + (ll)1e7 + 2) + 1) - (ll)1e7 - 1;break;}if(op >= 3) {cout << lst <<'\n';}}
}
结语
写完之后发现这东西没有其他平衡树那么有用
总之,这个算法的一些其他功能还有待发掘,期待各位神犇的进一步完善(或者之前有人发现了类似的算法可以分享一下)。
名字吗……没想好,各位给一下建议吧(如果没人发现过这个算法的话)。
