【第十五周】机器学习的学习笔记11 - 实践
文章目录
- 摘要
- Abstract
- 一、pytorch
- 1. torch.nn模块
- 1.1 损失函数
- 1.2 反向传播和优化器
- 2. 已有模型的使用
- 3. 完整模型训练
- 二、机器学习
- 1. 朴素贝叶斯
- 1.1 基本概念
- 1.2 朴素贝叶斯适用问题
- 1.3 案例:商品评论情感分析
- 2. 支持向量机SVM
- 2.1 算法定义
- 2.2 SVM计算过程和算法步骤
- 2.2.1 推导目标函数
- 2.2.2 目标函数的求解
- 总结
摘要
本周主要学习了Pytorch中的torch.nn模块中的损失函数和反向传播、利用已有模型进行迁移学习以及完整模型训练的实操。
机器学习部分学习了朴素贝叶斯模型和SVM支持向量机模型。朴素贝叶斯主要学习了基本概念,对概率论部分知识的回顾,以及项目实操。支持向量机学习了算法定义,目标函数的推导,目标函数求解等知识。
Abstract
This week, I mainly learned about the loss functions and backpropagation in the torch.nn module of PyTorch, transfer learning using pre-existing models, and also conducted practical operations on complete model training.
In the machine learning section, I studied the Naive Bayes model and the SVM (Support Vector Machine) model. For Naive Bayes, the learning content primarily included its basic concepts, a review of probability theory knowledge, and practical project implementation. For Support Vector Machines, I learned knowledge such as the algorithm definition, the derivation of the objective function, and the solution of the objective function.
一、pytorch
1. torch.nn模块
1.1 损失函数
作用:
①计算实际输出和目标之间的差距
②为反向传播的更新提供依据
#L1Loss
loss_1_1 = L1Loss(reduction='sum')
loss_1_2 = L1Loss(reduction='mean')
result_1_1 = loss_1_1(inputs,targets)
result_1_2 = loss_1_2(inputs,targets)
print(result_1_1)
print(result_1_2)
#MSELoss
loss_M = nn.MSELoss()
result_M = loss_M(inputs,targets)
print(result_M)
#CrossEntropyLoss交叉熵
x = torch.tensor([0.1,0.8,0.2])
y = torch.tensor([1])
#需要变换x维度,由3×1变换为1×3,否则无法与y进行运算
x = torch.reshape(x,(1,3))
loss_CEL = nn.CrossEntropyLoss()
result_CEL = loss_CEL(x,y)
print(result_CEL)交叉熵损失函数实际为与softmax函数结合: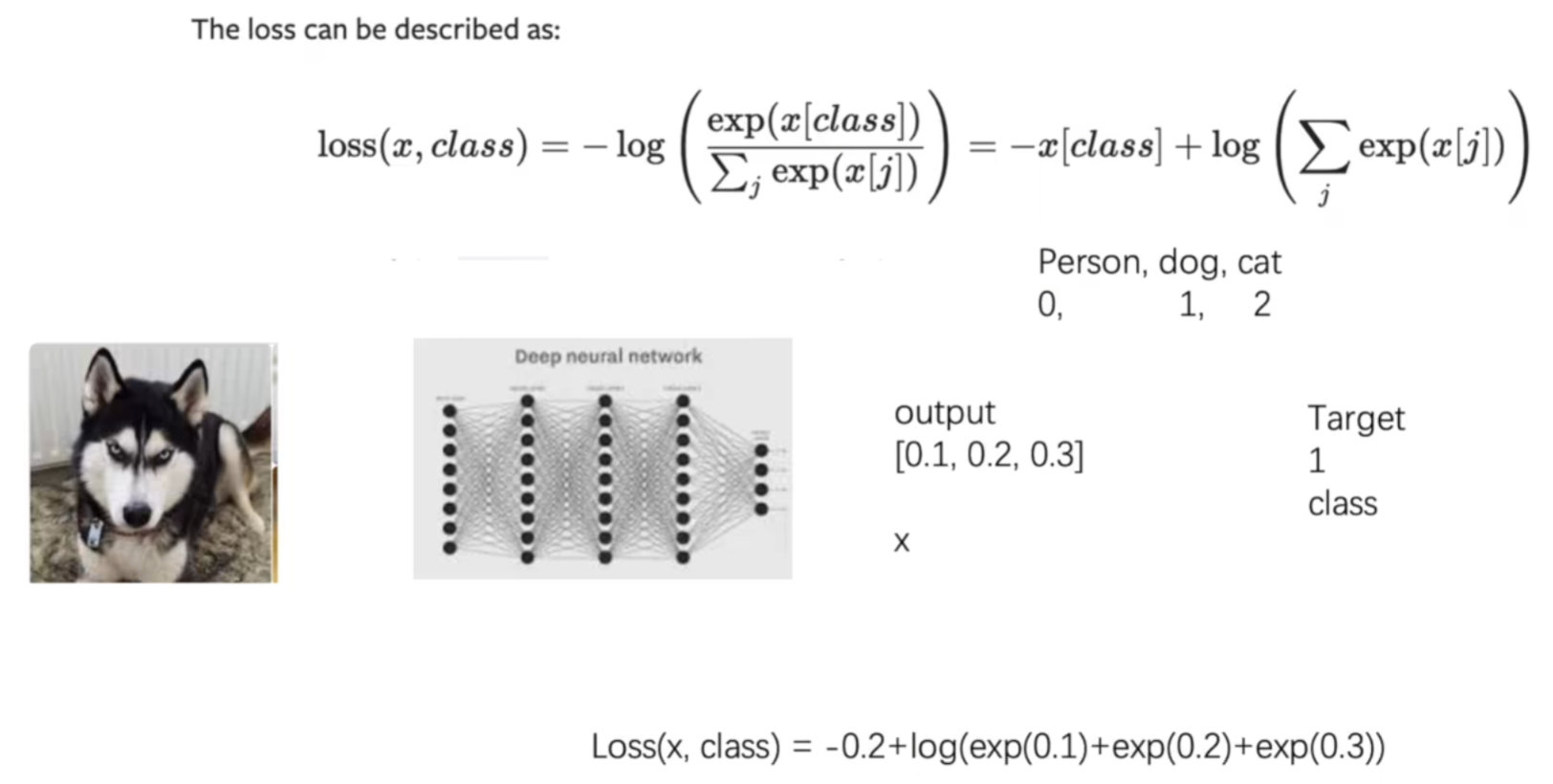
输出为各个类别的概率,target为目标类别,计算出的损失函数越小越好,因此当预测准确时输出最小。
1.2 反向传播和优化器
优化器:减小损失值,使预测接近目标。
#网络模型NeuralNet
model = NeuralNet()
loss = nn.CrossEntropyLoss()
#优化方法:随机梯度下降(SGD),lr为学习率
optim = torch.optim.SGD(NeuralNet.parameters(),lr=0.01)
#对所有数据进行多轮训练优化
for i in range(10):
run_loss =0.0
#对每一个数据进行一次优化,因此损失值变化不明显
for data in dataloader:
imgs,targets = data
outputs = model(imgs)
result_loss = loss(outputs,targets)
optim.zero_grad() # 每次都需要对梯度清0,否则容易对下一次梯度下降造成影响
result_loss.backward() #反向传播
optim.step() #进行优化
run_loss = run_loss + result_loss2. 已有模型的使用
VGG16模型:
VGG(
(features): Sequential(
(0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace=True)
(2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(3): ReLU(inplace=True)
(4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(5): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(6): ReLU(inplace=True)
(7): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(8): ReLU(inplace=True)
(9): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(10): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): ReLU(inplace=True)
(12): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(13): ReLU(inplace=True)
(14): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(15): ReLU(inplace=True)
(16): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(17): Conv2d(256, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(18): ReLU(inplace=True)
(19): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(20): ReLU(inplace=True)
(21): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(22): ReLU(inplace=True)
(23): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(24): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(25): ReLU(inplace=True)
(26): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(27): ReLU(inplace=True)
(28): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(29): ReLU(inplace=True)
(30): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(avgpool): AdaptiveAvgPool2d(output_size=(7, 7))
(classifier): Sequential(
(0): Linear(in_features=25088, out_features=4096, bias=True)
(1): ReLU(inplace=True)
(2): Dropout(p=0.5, inplace=False)
(3): Linear(in_features=4096, out_features=4096, bias=True)
(4): ReLU(inplace=True)
(5): Dropout(p=0.5, inplace=False)
(6): Linear(in_features=4096, out_features=1000, bias=True)
)
)在 VGG16 的实现中,开发者可能将网络分为多个逻辑部分:
- features:所有卷积层(特征提取)。
- avgpool:全局池化层(自定义添加,非原生)。
- classifier:全连接层(分类或回归)。
由使用文档可知VGG16训练模型的数据是ImageNet,ImageNet项目是一个用于视觉对象识别软件研究的大型可视化数据库。根据VGG16模型的神经网络可知最终将数据分为1000个类别,那么如何利用已训练好的模型特征对未训练的数据进行学习呢?
迁移学习
#导入VGG16模型
vgg16_true = torchvision.models.vgg16(weights='DEFAULT',progress = True)参数说明:
- weights:权重。'DEFAULT’表示使用默认预训练权重,若需使用特定版本的预训练权重需直接通过字符串指定(如 weights=‘IMAGENET1K_V1’)。
- progress:在下载模型权重时是否显示进度条。True表示显示下载进度条。
CIFAR10中共有10个类别,如何利用VGG16模型对该数据集进行学习:
#方法一:增加线性层
vgg16_true.classifier.add_module('add_linear',nn.Linear(1000,10))
#方法二:修改线性层
vgg16_true.classifier[6] = nn.Linear(4096,10)修改前: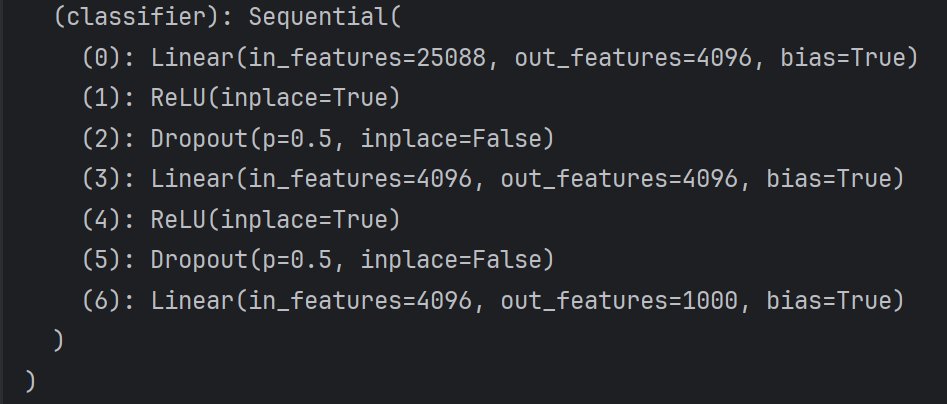
方法一修改后: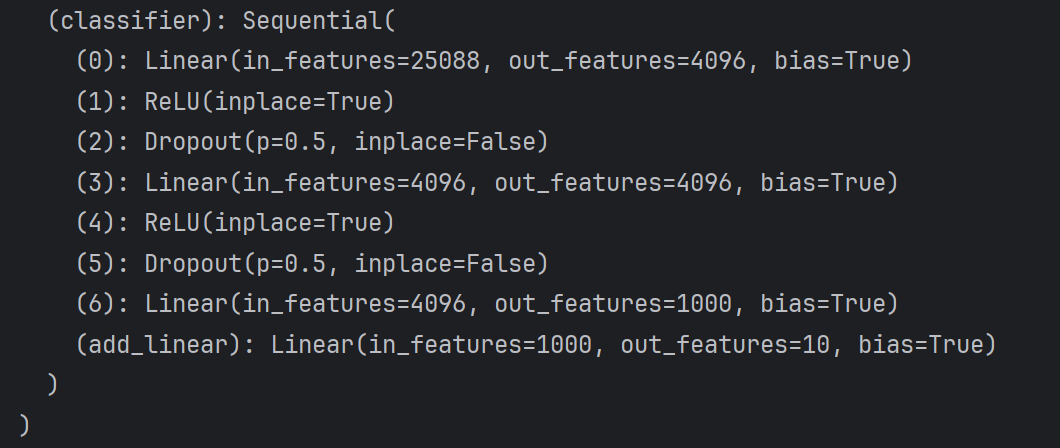
方法二修改后: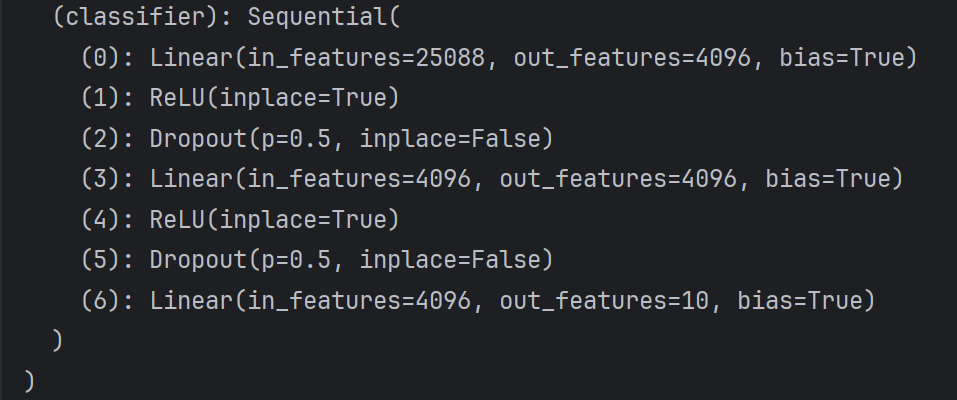
模型的保存
#保存方式1,模型结构+模型参数
torch.save(vgg16,"vgg16_method1.pth")
#保存方式2,模型参数
torch.save(vgg16.state_dict(),"vgg16_method2.pth")方式2所占用内存小于方式1
模型的加载
vgg16 = torchvision.models.vgg16(weights='DEFAULT',progress = True)
#方式1, 保存方式1,加载模型
model = torch.load("vgg16_method1.pth")
print(vgg16)
#方式2,加载模型
#model = torch.load("vgg16_method2.pth") 该种情况加载不是网络模型,而是字典数据类型,若要加载网络模型,需如下
vgg16 = torchvision.models.vgg16(weights='DEFAULT',progress = True)
vgg16.load_state_dict(torch.load("vgg16_method2.pth"))
print(vgg16)当加载自己定义的模型时,需要也要把模型复制到当前文件下,否则无法像已有模型进行加载。具体如下: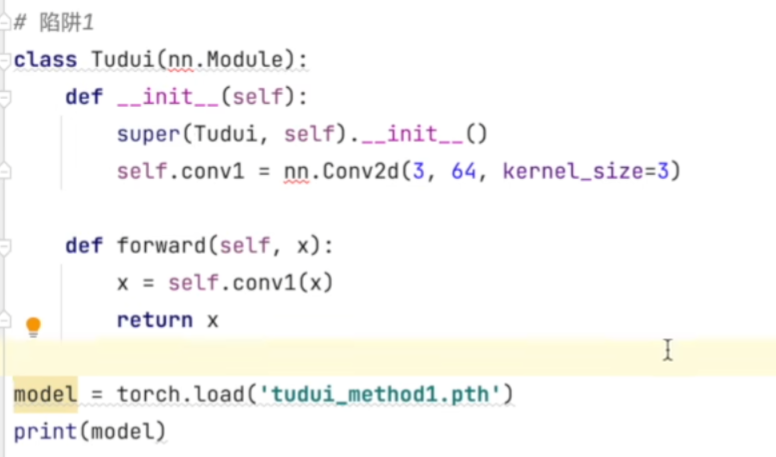
3. 完整模型训练
import torch
import torchvision.datasets
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter
from Model import *
#准备数据集
train_dataset = torchvision.datasets.CIFAR10("./vision_dataset",train = True,transform=torchvision.transforms.ToTensor(),download=True)
test_dataset = torchvision.datasets.CIFAR10("./vision_dataset",train = False,transform=torchvision.transforms.ToTensor(),download=True)
#查询数据集分类数量
train_dataset_size = len(train_dataset)
test_dataset_size = len(test_dataset)
print("训练集数据有{}个".format(train_dataset_size))
print("测试集数据有{}个".format(test_dataset_size))
#加载数据
train_dataloader = DataLoader(train_dataset,batch_size=64)
test_dataloader = DataLoader(test_dataset,batch_size=64)
#导入神经网络
model = NeuralNet()
#损失函数:交叉熵
loss_fn = nn.CrossEntropyLoss()
#优化器
#设置学习率
learning_rate = 1e-2 #0.01
optimizer = torch.optim.SGD(model.parameters(),lr=learning_rate)
#设置训练网络的一些参数
#记录训练的次数
total_train_step = 0
#测试次数
total_test_step = 0
#训练轮数
epoch = 10
writer = SummaryWriter()
for i in range(epoch):
print("这是第{}轮训练".format(i+1))
# 训练
model.train()
for data in train_dataloader:
imgs,targets = data
outputs = model(imgs)
loss = loss_fn(outputs,targets)
#优化器优化模型
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_train_step = total_train_step + 1
if total_train_step % 100 == 0:
print("训练次数:{},Loss:{}".format(total_train_step,loss))
writer.add_scalar("train_loss",loss.item(),total_train_step)
#测试(每训练完一轮就测试一次)
model.eval()
total_test_loss = 0
total_accuracy = 0
with torch.no_grad(): #with内的代码没有梯度
for data in test_dataloader:
imgs,targets = data
outputs = model(imgs)
loss = loss_fn(outputs,targets)
total_test_loss = total_test_loss + loss.item()
accuracy = (outputs.argmax(1) == targets ).sum()
total_accuracy = total_accuracy + accuracy
print("整体测试集Loss:{}".format(total_test_loss))
print("整体测试集上的正确率:{}".format(total_accuracy/test_dataset_size))
#可视化
writer.add_scalar("test_loss",total_test_loss, total_test_step)
writer.add_scalar("test_accuracy",total_accuracy/test_dataset_size,total_test_step)
total_test_step = total_test_step + 1
torch.save(model,"model_{}.pth".format(i))
print("模型已保存")
writer.close()- argmax(x),x=0代表以列为方向找到每列最大值的索引;x=1代表以行为方向找到每行最大值的索引。
- eval()模型进入验证状态,train()模型进入训练状态。且只在特定层(Dropout,BatchNorm)有作用,因此方法可以只在模型中存在上述特殊层才加入。
GPU训练模型是将网络模型,数据,损失函数转移大GPU上训练:
方法一:cuda()方法
方法二:to(device)
二、机器学习
1. 朴素贝叶斯
1.1 基本概念
联合概率、条件概率和相互独立
联合概率:包含多个条件,且所有条件同时成立的概率。P(A,B)
条件概率:在事件A在另一个事件B已经发生条件下的发生概率。P(A|B)
相互独立:如果P(A,B)=P(A)P(B),则A,B相互独立。若各个属性相互独立,则P(A,B|C)=P(A|C)P(B|C)。
贝叶斯公式:
当样本数量不充足,但需要判断某一事件的发生概率,那么可以假设各个条件之间相互独立,即朴素贝叶斯。
拉普拉斯平滑系数用于解决由样本数不足引起的不合理的事件发生概率。
1.2 朴素贝叶斯适用问题
文本分类:通过分析文本中的词汇、短语等特征,利用朴素贝叶斯算法判断文本。类别。
- 垃圾邮件识别
- 情感分析
- 新闻分类
1.3 案例:商品评论情感分析
#1,获取数据
data = pd.read_csv("./书籍评价.csv",encoding="gbk")
#2,数据基本处理
#2.1 取出内容,对数据进行分析
content = data["内容"]
content.head()
#2.2 评判
#读取评价列,好评记作1,差评记作0
data.loc[data.loc[:,"评价"]=='好评','评价符号']=1
data.loc[data.loc[:,"评价"]=='差评','评价符号']=0
#data.head()
good_or_bad = data["评价"].values
print(good_or_bad)
#2.3选择停用词.停用词表(如常见的无意义词汇 "的"、"是"、"在" 等),这些词会在处理过程中被过滤掉。
#加载停用词
stopwords = []
with open('./stopwords.txt','r',encoding='utf-8') as f:
#按行读取
lines = f.readlines()
print(lines)
for tmp in lines:
line = tmp.strip() #除去字符两端空白字符
print(line)
stopwords.append(line)
#对停用词去重
stopwords = list(set(stopwords)) #去重
print(stopwords)
#2.4 把“内容”处理,转化成标准格式
comment_list = []
for tmp in content:
print(tmp)
#把一句话变成一个个词
seg_list = jieba.cut(tmp,cut_all = False)
seg_str = ','.join(seg_list) #使用“,”隔开分割词
print(seg_str)
comment_list.append(seg_str)
#2.5统计词的个数
# CountVectorizer 将文本中的词语转换为词频矩阵
con = CountVectorizer(stop_words= stopwords)
#进行词数统计
X = con.fit_transform(comment_list) #计算各个词出现的次数
name = con.get_feature_names_out() #获取词袋所有文本关键字
print(X.toarray())
print(name)
#2.6准备训练集和测试集
x_train = X.toarray()[:10,:] #选取前十行
y_train = data["评价"][:10]
#测试集
x_test = X.toarray()[10:,:] #选取十行后的数据
y_test = data["评价"][10:]
#3模型训练
mb = MultinomialNB(alpha=1)
mb.fit(x_train,y_train)
y_pre = mb.predict(x_test)
print("预测值:",y_pre)
print("真实值:",y_test)
#模型评估
print(mb.score(x_test,y_test))步骤分析以及使用的方法说明:
(1)获取数据
(2)数据基本处理
①取出内容列,对数据进行分析
②判定评判标准
③选择停用词。
停用词:如常见的无意义词汇 “的”、“是”、“在” 等,这些词会在处理过程中被过滤掉。
④内容处理,转换格式
jieba.cut()jieba.cut ()方法基于词典(覆盖日常用语、专业术语等)将连续的中文字符切分为有意义的词语,匹配规则:按最长匹配原则,优先匹配词典中存在的词语。示例:“清华大学”会整体切分(词典中存在),而不是“清华/大学”。,接受三个输入参数:
1,需要分词的字符串
2,cut_all 参数用来控制是否采用全模式。它支持三种分词模式:精确模式、全模式和搜索引擎模式,满足不同场景下的需求。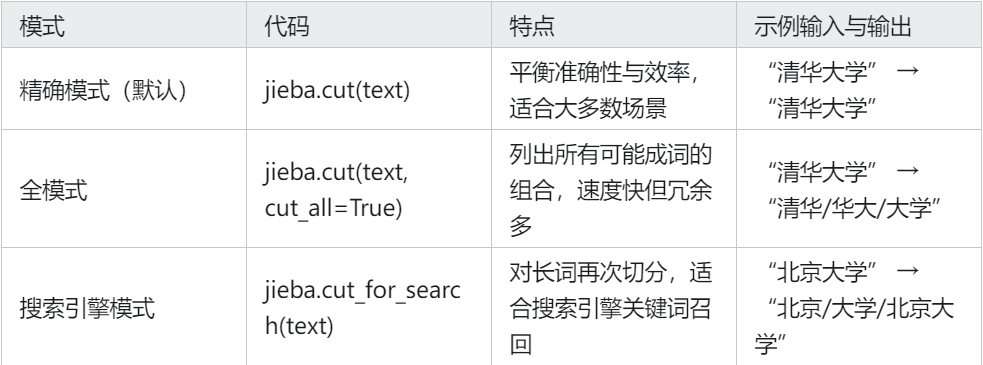
3,HMM 参数用来控制是否使用 HMM 模型
隐马尔可夫模型(HMM):识别未登录词(词典中未收录的词),例如人名、网络新词。
⑤统计词的个数
fit_transform()主要用于对训练数据执行拟合和转换操作,核心步骤:
fit:分析文本数据,构建词汇表(记录所有出现的有意义词汇)。
transform:将每个文本转换为基于词汇表的词频向量,最终形成一个矩阵X(形状为:文本数量 × 词汇表大小),矩阵中的每个元素表示某个词在某篇文本中出现的次数。
get_feature_names_out()获取构建的词汇表,返回一个数组,其中包含所有被纳入词频矩阵的词汇(即fit过程中提取的有意义词汇,已过滤停用词)。
⑥准备训练集和测试集
(3)模型训练
1,初始化多项式朴素贝叶斯模型
MultinomialNB(alpha=1)创建了一个多项式朴素贝叶斯分类器实例,其中:
alpha=1表示使用拉普拉斯平滑(Laplace smoothing),用于避免在计算概率时出现零概率的情况(当某个特征在训练集中未出现时)。alpha 值越大,平滑效果越强。
2,训练模型
fit()通过适配数据生成模型参数。其核心功能是调整算法参数以匹配输入数据特征,最终生成可用于预测的模型。
(4)模型评估
2. 支持向量机SVM
2.1 算法定义
SVM支持向量机:寻找一个超平面将样本分为两类,并且间隔最大。SVM能够执行线性或非线性分类、回归,甚至异常值检测任务,适用于中小型复杂数据集分类。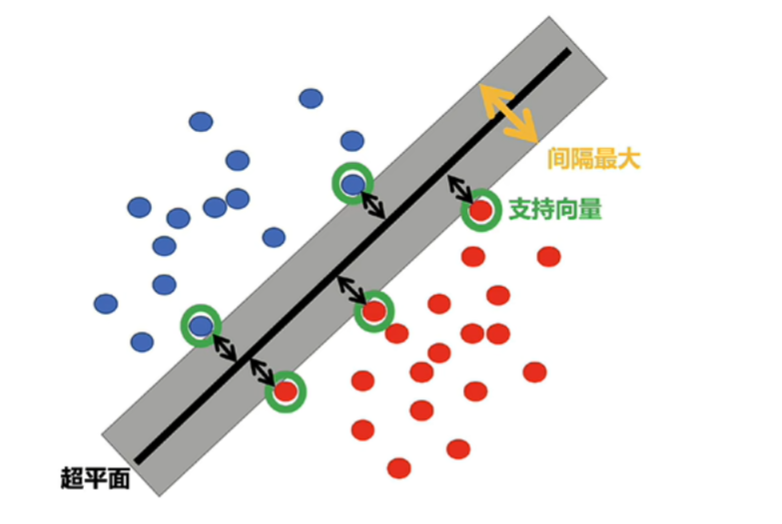
支持向量:构建足够宽的超平面落在平面上的点就是支持向量
间隔:
软间隔:允许存在少数分类不正确的样本。尽可能保持最大间隔宽度和限制间隔违例(位于最大间隔之上,甚至在错误一边的实例)之间找到良好的平衡。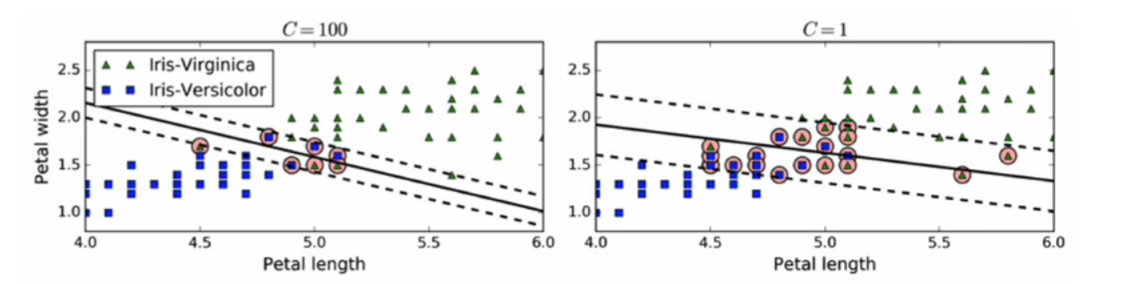
注:C表示惩罚因子,衡量间隔宽度。C值越大间隔越小,间隔违例较少;C值越小间隔越大。
硬间隔:必须将所有样本分类正确。只在数据是线性可分离的时候有效,对异常值非常敏感。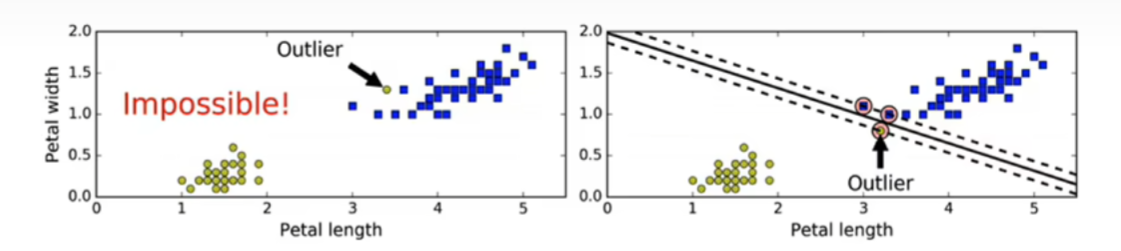
算法原理
数据要求: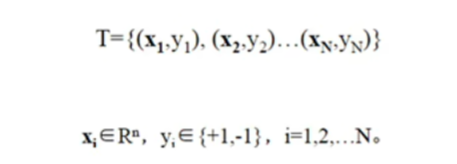
其中y=1时,xᵢ为正例;y=-1,xᵢ为负例。y的值设置为-1,1为方便后续运算。
线性可分支持向量机
将数据集通过间隔最大化得到的分离超平面: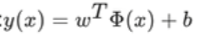
相应的分类决策函数,即线性可分支持向量机: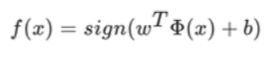
Φ(x):某个确定的特征空间转换函数,将x映射到更高的维度,即核函数。举例说明:
当有两个特征:x₁,x₂组成最常见的线性函数:w₁x₁+w₂x₂,由于数据不能被很好表示,因此函数变为:w₁x₁+w₂x₂+w₃x₁x₂+w₄x₁x₁+w₅x₂x₂,于是多出三个特征。
一般Φ(x)=x
2.2 SVM计算过程和算法步骤
2.2.1 推导目标函数
当Φ(x)=x,决策边界的表达式为 WᵀX + b = 0。W = (w₁, w₂, …, wₙ)ᵀ 是系数向量,X = (x₁, x₂, …, xₙ)ᵀ 是空间中的点。此时W为法向量:
证明:
WᵀX₁ + b = 0
WᵀX₂ + b = 0 两式相减可得:Wᵀ(X₁ - X₂) = 0。
其中,X₁ - X₂是超平面上的任意一条方向向量(两点连线),而Wᵀ · (X₁ - X₂) = |Wᵀ| × |X₁ - X₂| × cosα =0表示W与该方向向量的点积为 0,即W与超平面上的所有方向向量都垂直。
因此W为法向量。b为位移项,决定了超平面与远点的距离。样本空间中任意点x到超平面(w,b)的距离为: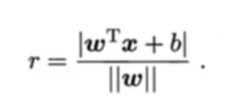
式子说明:
分子 | wᵀxᵢ + b |是点 x 代入超平面方程后结果的绝对值(因为分类在超平面下方时为负值,所以需要使用绝对值);
分母 (||w||) 是法向量 w 的范数(可以简单理解为法向量的 “长度”)。
补充:“范数”
假设超平面能将样本分类正确,对于(xᵢ,yᵢ)∈D,若
yᵢ = +1,则有wᵀxᵢ + b > 0
yᵢ = -1,则有wᵀxᵢ + b < 0整理式子可以得到:
yᵢ = +1,wᵀxᵢ + b >= +1
yᵢ = -1,wᵀxᵢ + b <= -1,注:
①支持向量使上述式子等号成立。两个异类支持向量到超平面距离之和为:γ = 2 / ||W||,即间隔。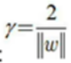
②yᵢ ( wᵀxᵢ + b ) >= 1恒成立,因此约束表达式可以进一步提炼为 yᵢ ( wᵀxᵢ + b ) >= 1 ,其中y为分类值,约束表达式均为仿射函数约束。
补充:
仿射函数概念:最高次数为1的多项式函数,其一般形式为f(x)=Ax+b,其中A为m×k矩阵,b为m维向量。当b=0时称为线性函数。
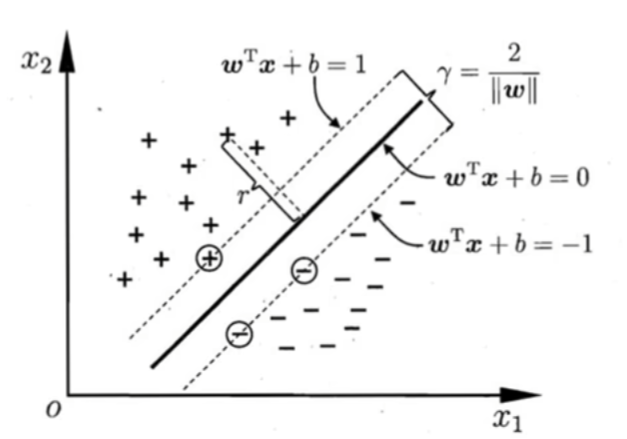
若要找到具有最大间隔的划分超平面,则需使得γ最大,并由此推导出目标函数:
注:目标函数改为÷2的方式是为了方便计算,后续需要求导,求导后系数为1
2.2.2 目标函数的求解
使用拉格朗日乘子法求解目标函数最优值。
拉格朗日乘子法:一种寻找多元函数在一组约束下的极值的方法。可以将d个变量与k个约束条件的最优化问题转化为具有 d+k 个变量的无约束优化问题求解。
当没有约束的时候,我们可以直接令目标函数的导数为零,求最优解。
有约束,最直观的办法就是把约束放进目标函数里。拥有几个约束就引入几个拉格朗日乘子λ,构造新函数,拉格朗日函数h(x)。
仿射函数约束是等式可以直接使用拉格朗日乘子,若为不等式则需要添加一个非负变量将不等式转化为等式约束,再使用拉格朗日乘子法。如下:
说明:
①:①式子为不等式约束
②:将①转换为等式约束
③:拉格朗日方程式。为目标函数使用拉格朗日最值法求最值。
KKT条件
(1)基本KKT条件
接着求最值,对拉格朗日方程式所有自变量进行求导,并且偏导等于0。
说明:后面将③式带入④式得到横线处式子,而根据横线处式子可以推出两种情况:
λᵢ = 0,yᵢ ( wᵀxᵢ + b ) -1 > 0
λᵢ ≠ 0,yᵢ ( wᵀxᵢ + b ) -1 = 0(2)惩罚系数λ的分析:
将λᵢ看作违背约束条件的惩罚系数,当yᵢ ( wᵀxᵢ + b ) - 1 < 0 , 如果 λᵢ < 0 ,则拉格朗日式子后半部分小于0,虽然此时拉格朗日方程式会变更小,但违反约束条件yᵢ ( wᵀxᵢ + b ) -1 >= 0 。因此推测:λᵢ >= 0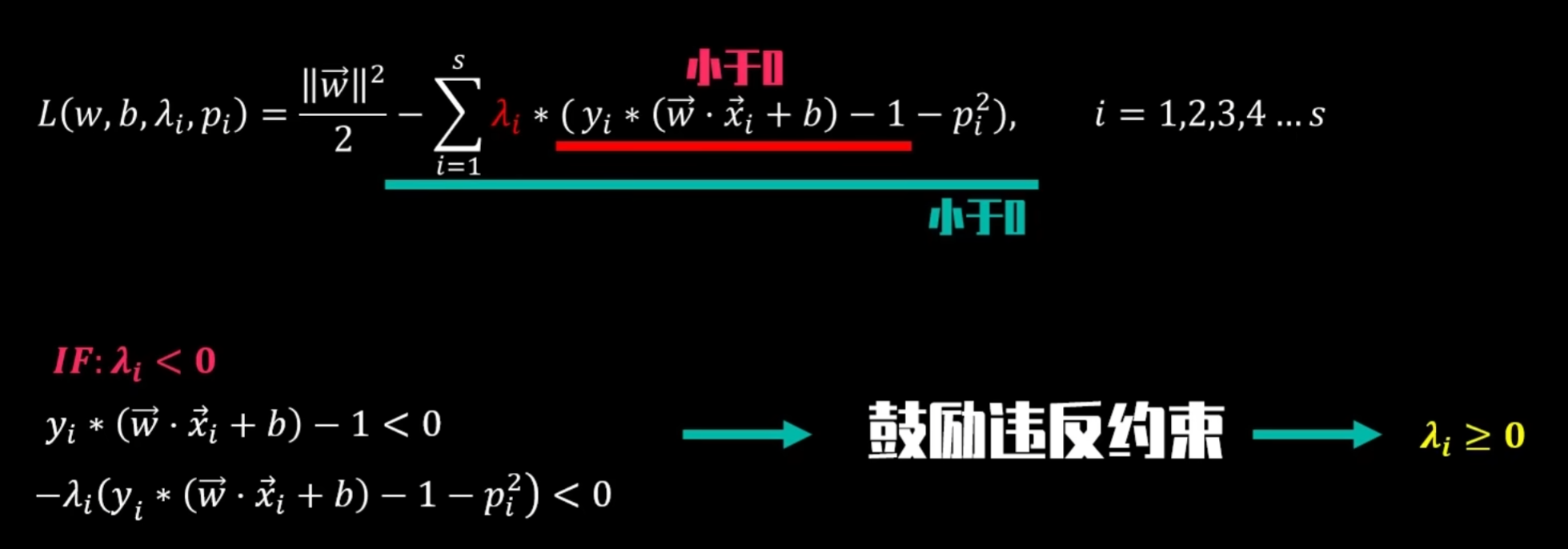
分别绘制目标函数和约束条件函数的图片,可以得出当只有一个约束的时候,两者交点处可以求得最小值,并且此时目标函数与条件约束函数的梯度方向相同,大小通过>0的λ来调整。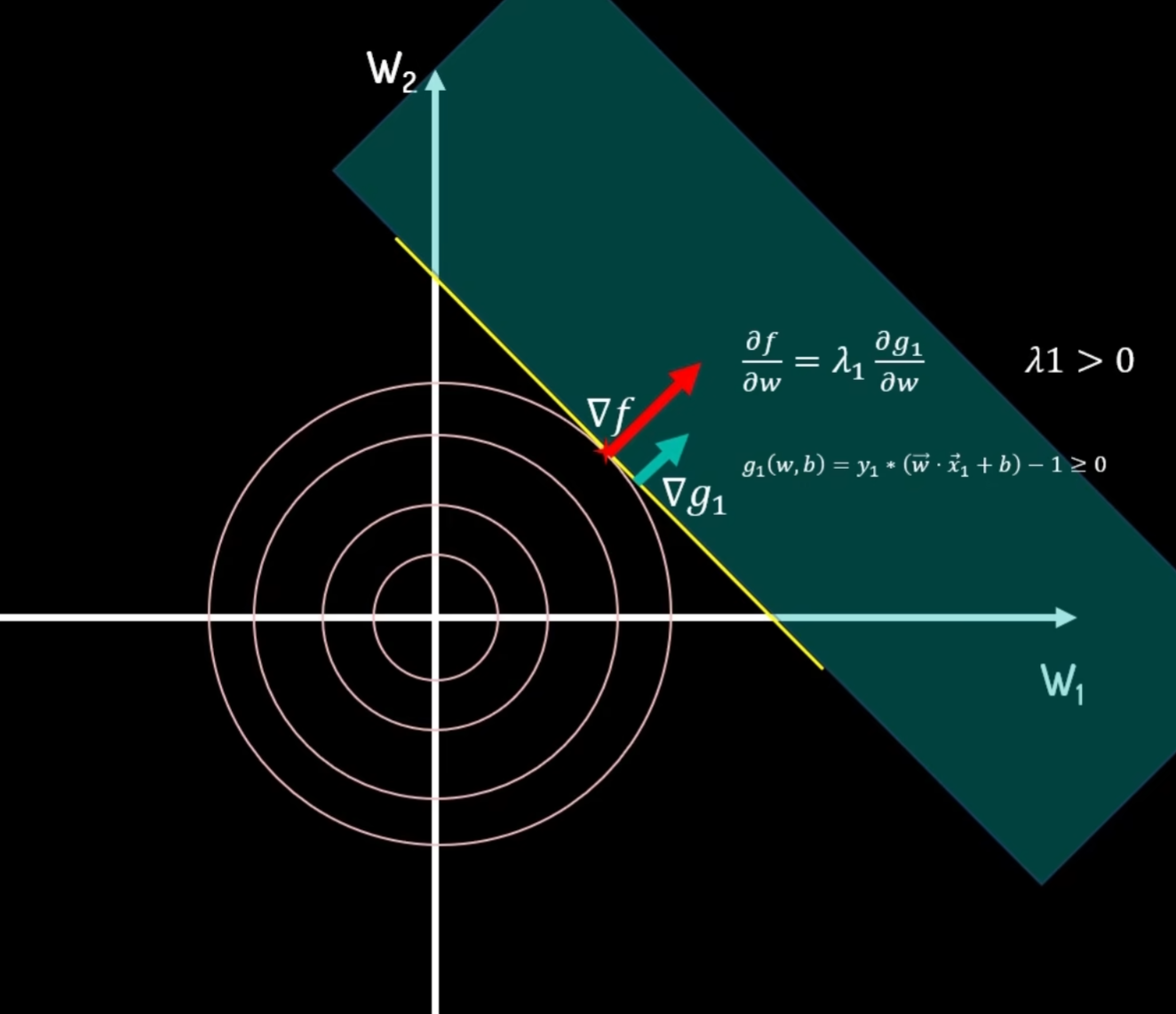
需要注意:
梯度方向:等高线在该点的法线方向,而非切线方向。
当有两个约束条件时,两个约束边界的相交点为最优解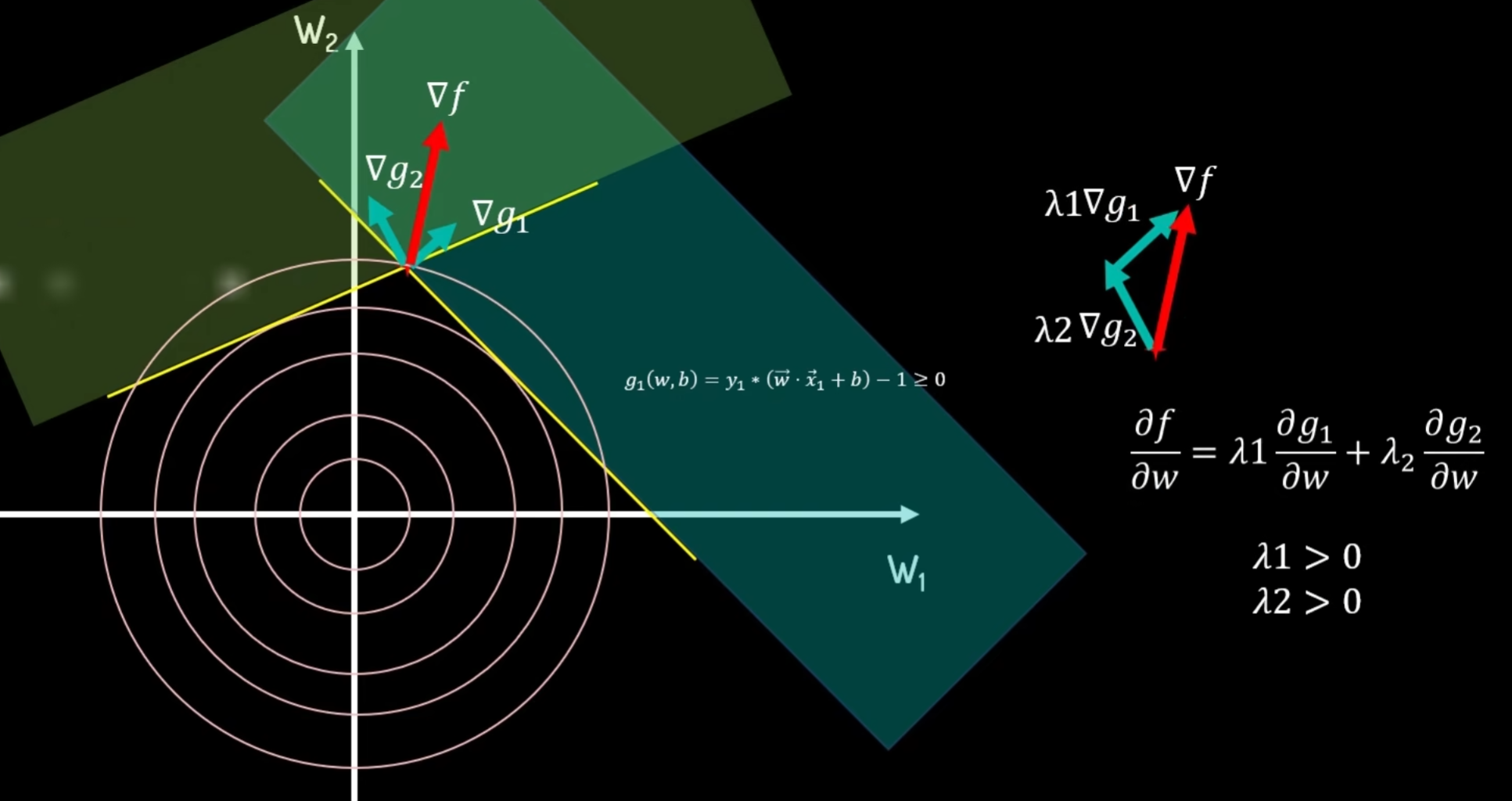
当最优解不在约束条件的边界上时,约束条件不起实质性作用,λ= 0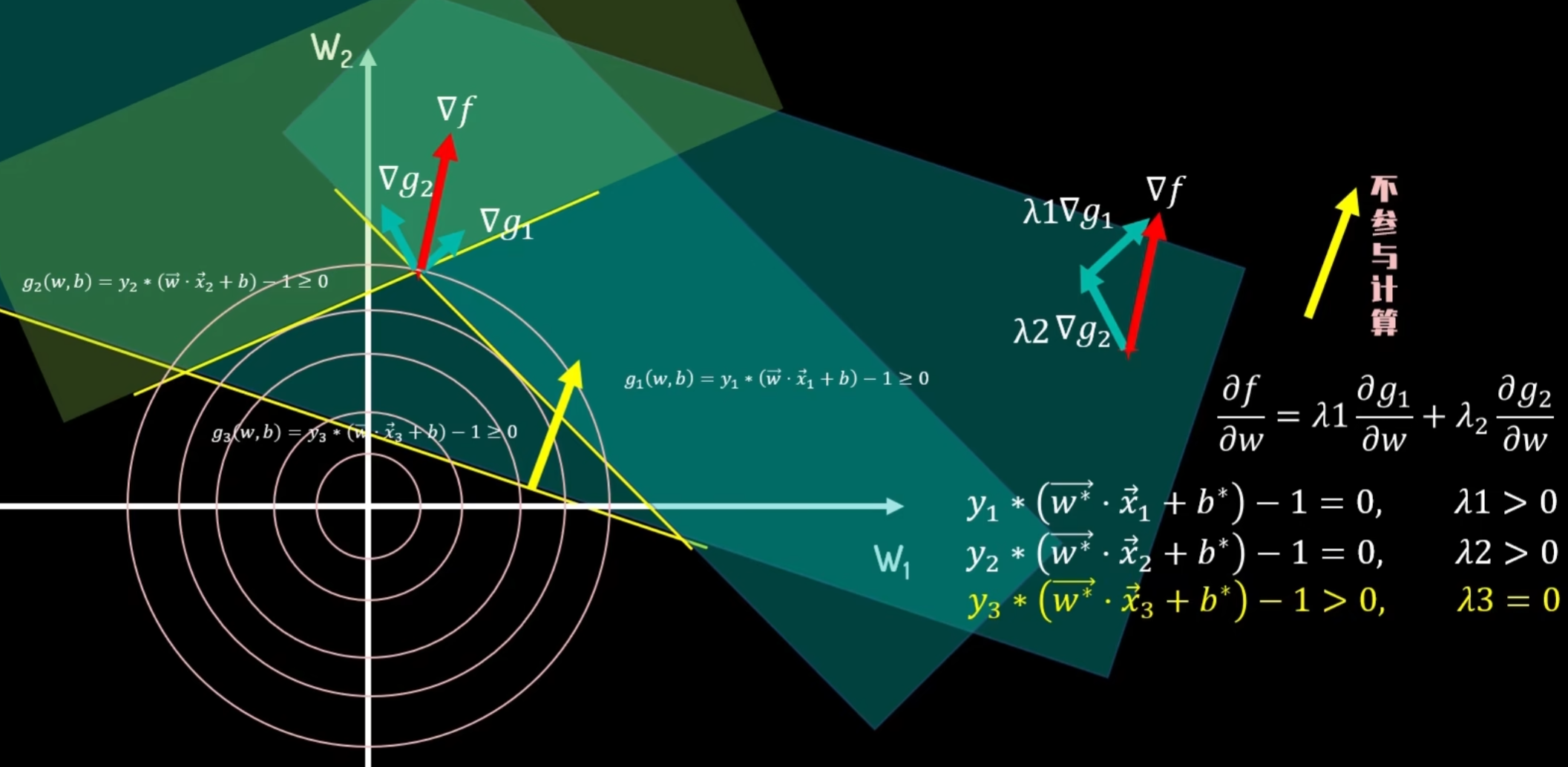
综合上述所有条件即为KKT条件: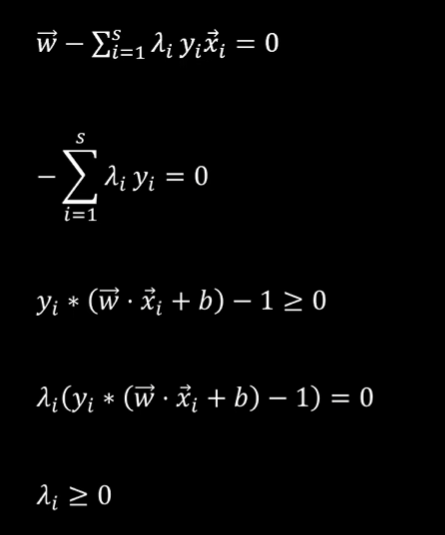
对偶性
对偶问题是与原优化问题紧密相关的另一个优化问题,通过研究对偶问题,可以更好地理解原问题的性质。
注意:此时拉格朗日方程式中自变量没有q。
此时满足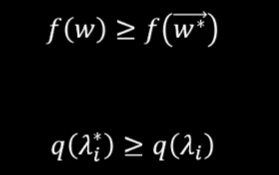
使用具体案例理解对偶性:例如下面将求解一个函数的最小值转换为求解另一个函数的最大值。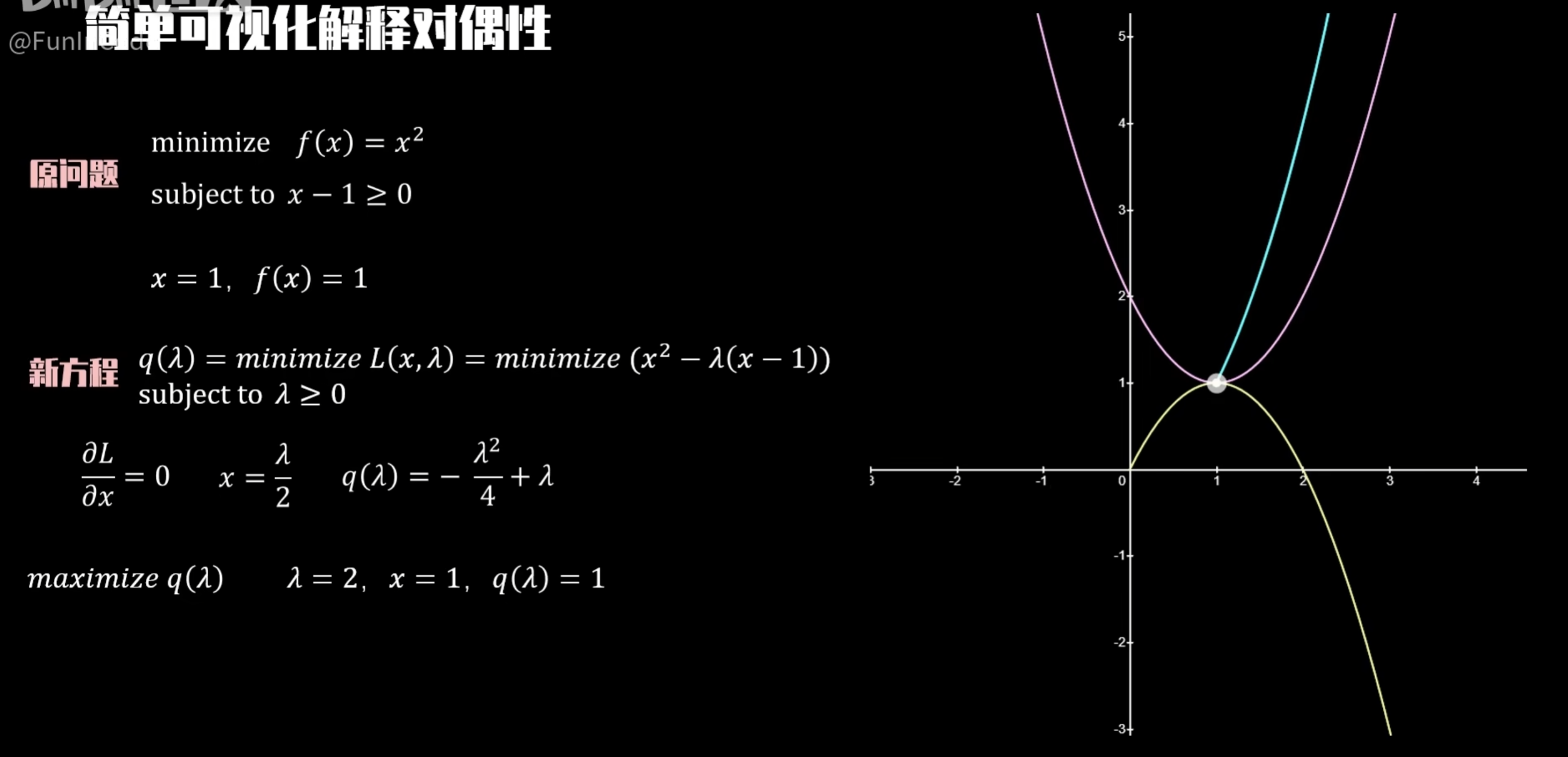
转向抽象问题理解
根据KKT条件进行相应代换

核技巧
核技巧(Kernel Trick):提供高维度向量相似度测量,但不需要知道具体转化维度函数。避免将数据送到高维度进行计算,但是可以获得高维度分类结果。
升维原因:当原维度下决策超平面无解,此时可以通过维度转换函数进行升维处理,可以在新维度很好解决问题。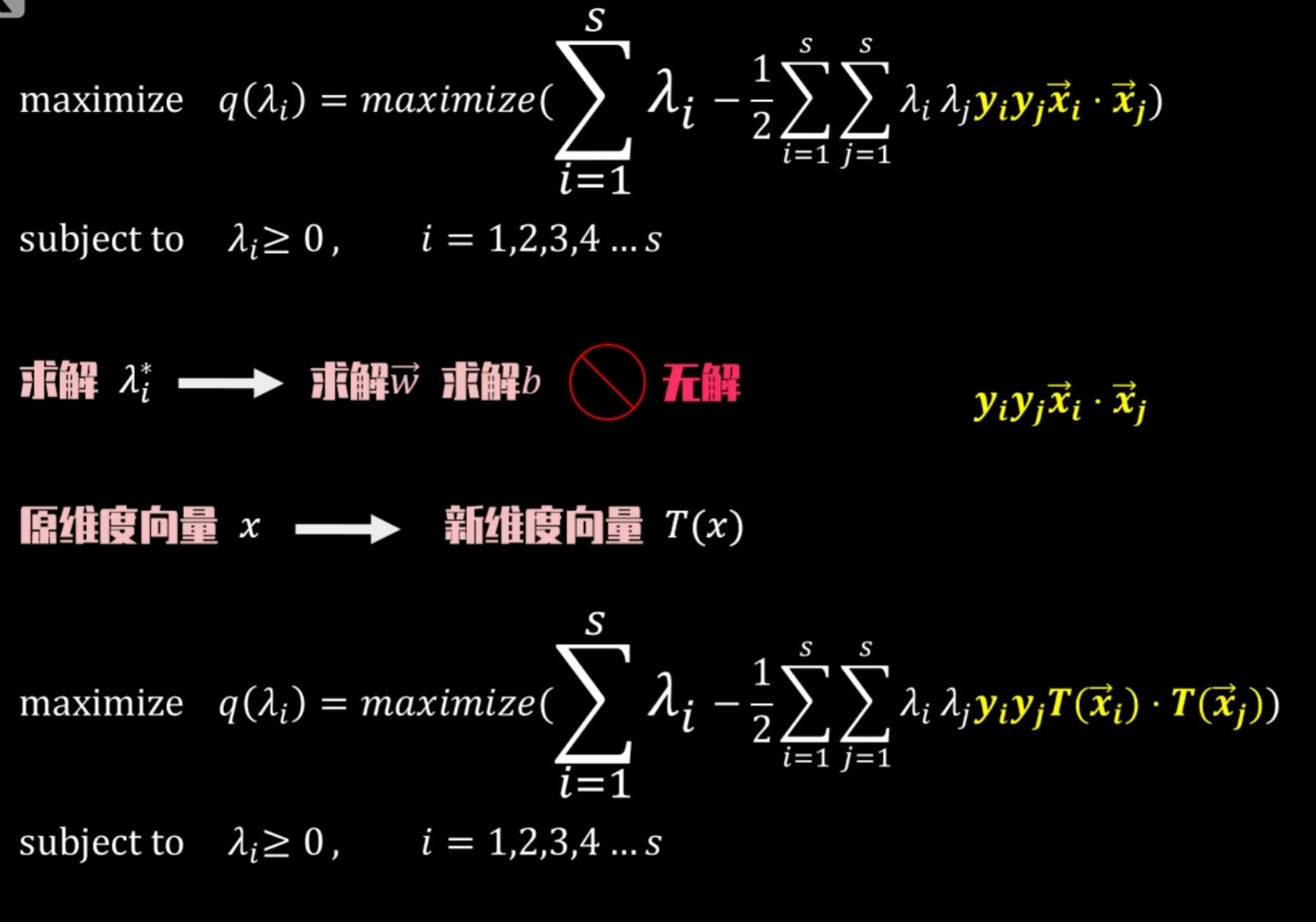
如何得到升维后的点积结果?存在下列两种方法:
方法一:直接求升维后向量的点积
方法二:使用二维向量点击结果计算
多项式核函数中的c必不可少,因为c的存在使得最终点积结果才包含了从低次项到高次项的数据组合,体现维度多样性。
若要二维转无穷维应如何进行?
此时使用方法一:升维后向量点积 无法行通,所有应使用高斯核函数RBF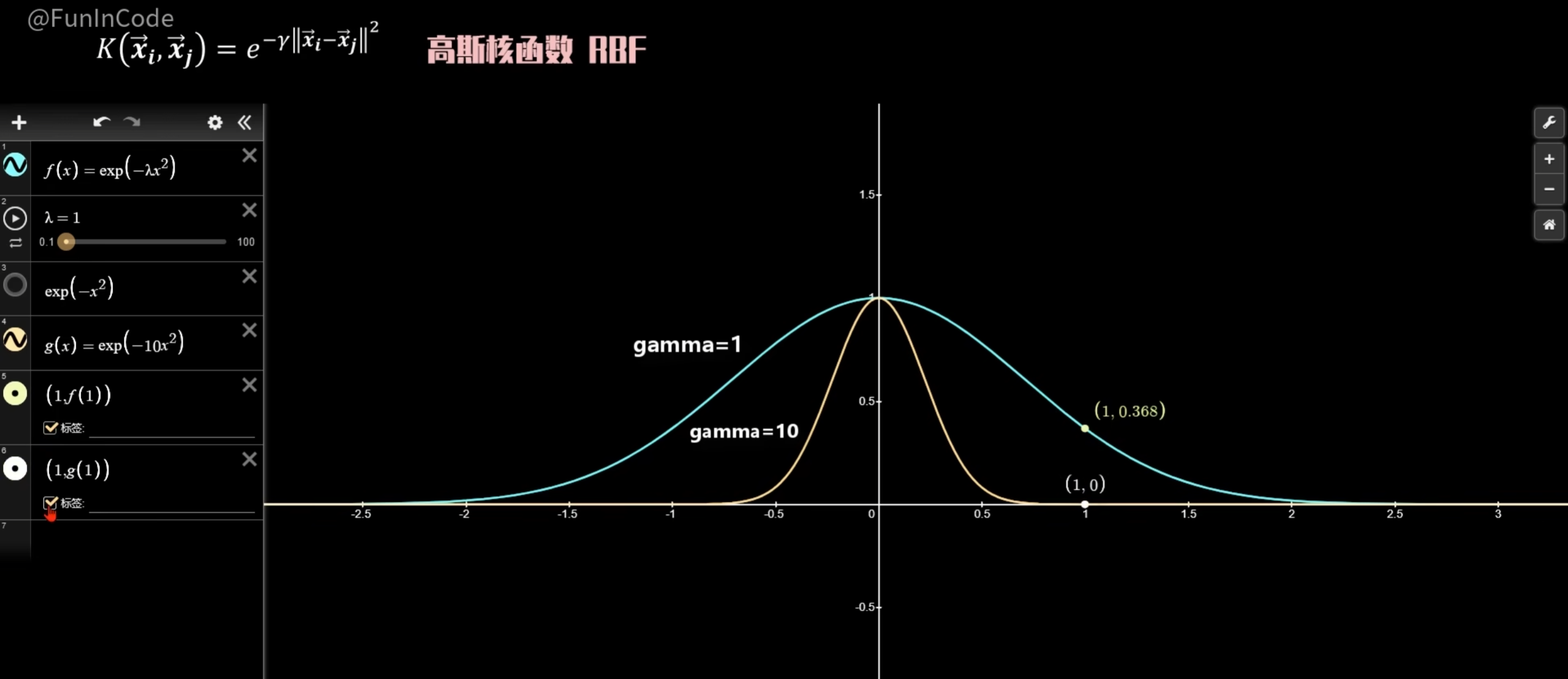

说明:γ越大表示越严格,因此同样距离在γ=1下面可能认为相似度高,在γ=10下面相似度就低了。
高斯核函数推导: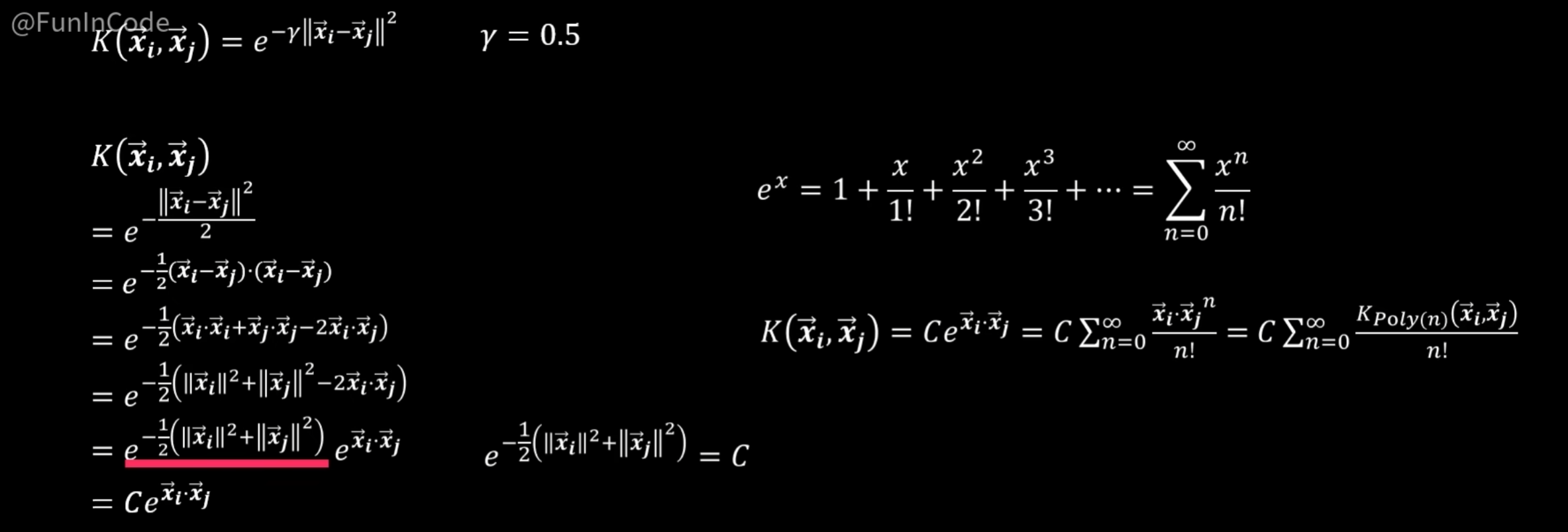
说明:
①由于特征已经确定好了,因此特征相关的数值视作常数C,点乘中包含了未知的超平面信息,所以无法视作常数运算。
②引入泰勒级数实现了在不实质性踏入无限维度的情况下得到无限维度下向量相似度的结果。
总结
本周在SVM模型的数学推导过程中花费了大量时间去理解过程,下周将会开展SVM模型实操。
SVM的讲解观看该视频受益匪浅,遂进行记录【数之道25】机器学习必经之路-SVM支持向量机的数学精华
