最小乘积模型用于分析+证明凸包,快速凸包构造用于求解凸包
将一种方案看作点 \((a,b)\),那么取到最小值的方案一定在左下凸包上。
现在考虑如何快速求解凸包.
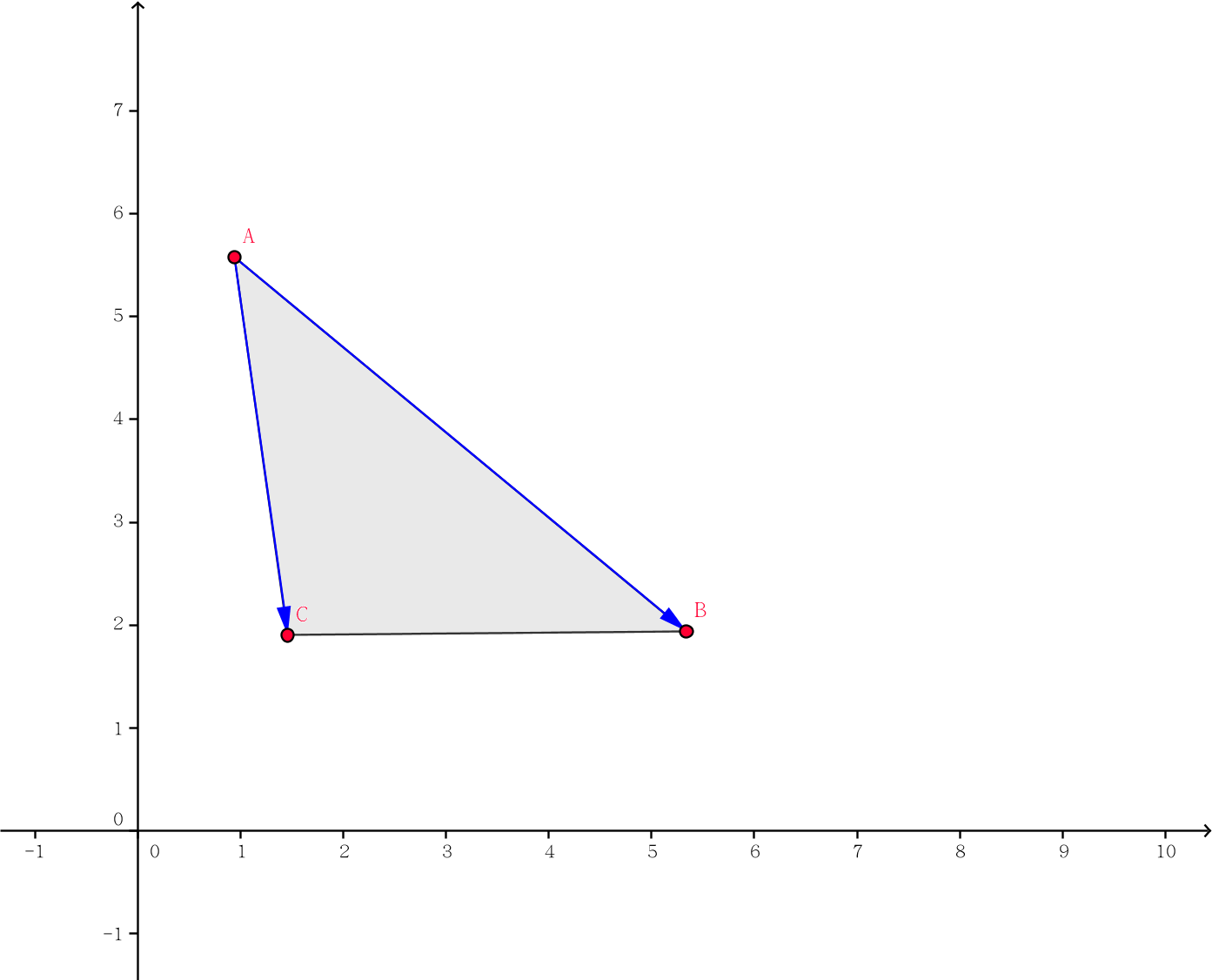
如图每次找到使三角形面积最大的,迭代即可。
复杂度证明:
结论:值域为 \(V\) 的整平面的不共线凸包最多只有 \(O(V^{\frac 23})\) 个点。
首先考虑右下凸包。假设有 \(T\) 个点,第 \(i\) 个点与第 \(i+1\) 个 的既约斜率为 \(\frac {y_{i+1}-y_i}{x_{i+1}-x_i}=\frac {p_i}{q_i}\),设 \(y_{i+1}-y_i=p_i\times t,x_{i+1}-x_i=q_i\times t\),则 \(y_{i+1}-y_i+x_{i+1}-x_i=t(p_i+q_i)\ge p_i+q_i\)。
所以
又因为
所以
当 \(p_i+q_i\) 取值越小,\(T\) 的取值越大。
\(T\) 的最大值为满足 \(\sum_{i=1}^{T}(p_i+q_i)> 2V\) 的最小的 \(T\),其中 \(\{\frac{p_i}{q_i}\}\) 为有理数集合。
考虑将所有既约分数分子分母和排列成数列:
则数列单调不降,且数字 \(t\) 出现 \(\sum_{1\le u\le t-1}[u\bot t-u]< t\) 次,构造数列 \(\{b\}\) 使得数字 \(t\) 恰好出现 \(t\) 次,则 \(\{b\}\) 的前缀和一定小于原数列的同一位置前缀和。
假设原数列前 \(i\) 项和为 \(F_i\) 数列 \(\{b\}\) 的前 \(i\) 项和为 \(S_i\),令 \(t=\lfloor \sqrt T\rfloor\),则:
所以满足条件的 \(T=O(V^{\frac{2}{3}})\)。
这个快速凸包构造也可以用在高维的情况,但是不会复杂度证明。
P5540 [BalkanOI 2011] timeismoney - 洛谷
https://www.luogu.com.cn/problem/P6158
P11706 「KTSC 2020 R1」穿越 - 洛谷
