策略梯度方法(Policy Gradient Methods)
背景
在基于值函数的方法(如 DQN)中,直接逼近 Q 值存在多种问题:
- Q 值无界:可能取任意实数(正或负),输出层必须是线性的;
- Q 值方差大:不同 \((s,a)\) 对的 Q 值差异巨大,神经网络难以拟合;
- 仅适用于离散动作空间:在连续动作空间中无法直接求最大动作。
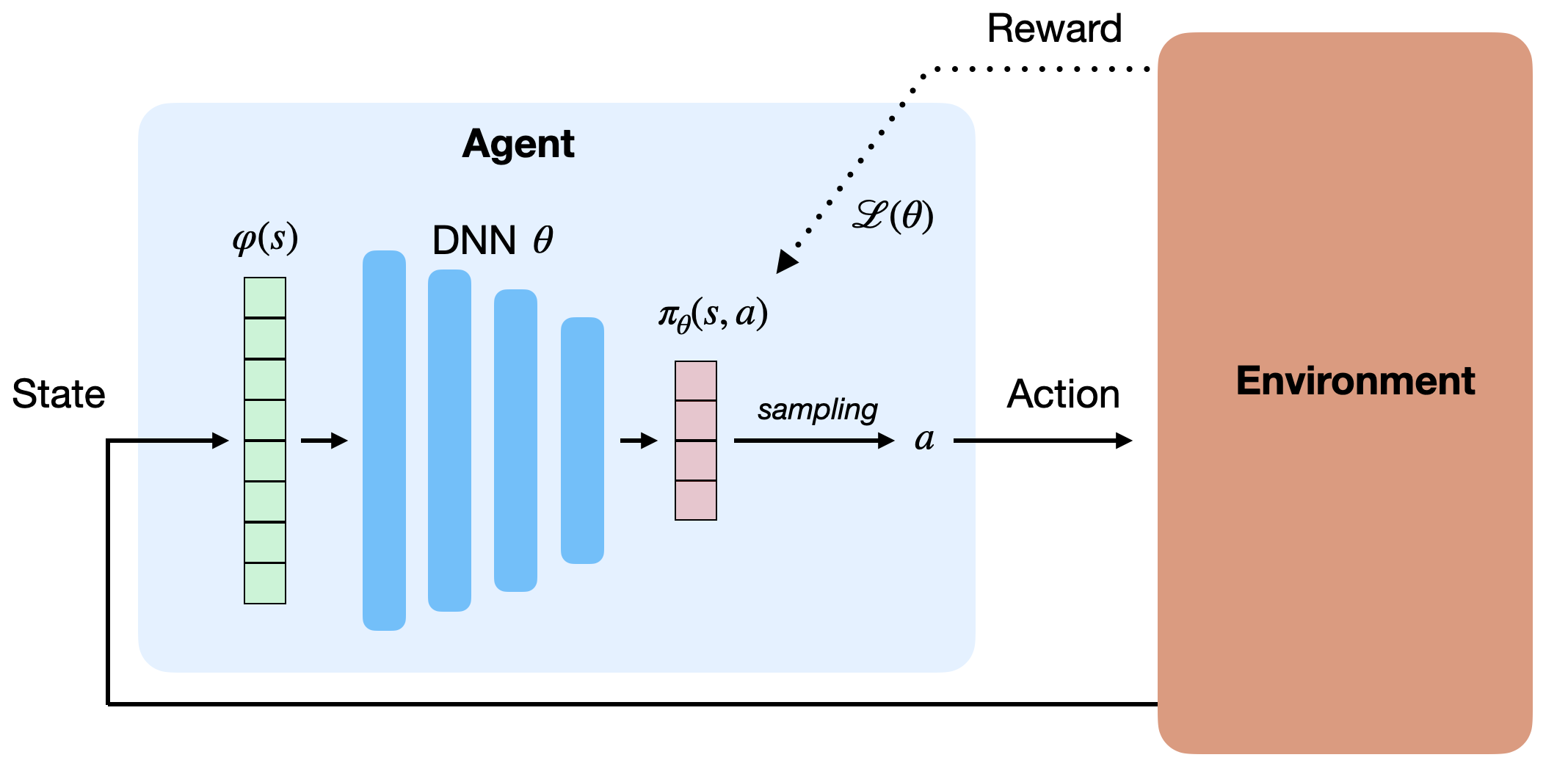
因此,可直接逼近策略 \(\pi_\theta(s,a)\),即用神经网络输出动作概率或连续控制信号。
这类网络称为参数化策略(Parameterized Policy)。
- 对离散动作空间:输出层通常为 softmax,表示每个动作的概率;
- 对连续动作空间:输出层可直接生成动作值(如机械臂角度)。
![policysearch]()
策略搜索(Policy Search)
策略搜索直接学习参数化策略 \(\pi_\theta\),目标是最大化由该策略生成的轨迹的期望回报:
\[J(\theta) = \mathbb{E}_{\tau \sim \rho_\theta}[R(\tau)] = \mathbb{E}_{\tau \sim \rho_\theta}\left[\sum_{t=0}^T \gamma^t r(s_t, a_t, s_{t+1})\right]
\]
其中轨迹 \(\tau = (s_0,a_0,s_1,a_1,\ldots,s_T,a_T)\) 的概率为:
\[\rho_\theta(\tau) = p_0(s_0) \prod_{t=0}^T \pi_\theta(s_t,a_t) p(s_{t+1}|s_t,a_t)
\]
目标函数可表示为积分形式:
\[J(\theta) = \int_\tau \rho_\theta(\tau) R(\tau) d\tau
\]
利用 Monte Carlo 采样,可近似计算目标函数:
\[J(\theta) \approx \frac{1}{N} \sum_{i=1}^N R(\tau_i)
\]
但这种方法存在高方差、样本效率低、仅限回合式任务等问题。
为优化 \(J(\theta)\),我们使用梯度上升:
\[\theta \leftarrow \theta + \eta \nabla_\theta J(\theta)
\]
关键问题是如何估计策略梯度 \(\nabla_\theta J(\theta)\)。
REINFORCE 与 DPG(确定性策略梯度)等算法提供了相应的估计方法。
REINFORCE 算法
策略梯度推导
@Williams1992 提出利用对数技巧(log-trick)估计策略梯度。
从定义出发:
\[\nabla_\theta J(\theta) = \nabla_\theta \int_\tau \rho_\theta(\tau) R(\tau) d\tau = \int_\tau (\nabla_\theta \rho_\theta(\tau)) R(\tau) d\tau
\]
利用恒等式:
\[\nabla_\theta \rho_\theta(\tau) = \rho_\theta(\tau) \nabla_\theta \log \rho_\theta(\tau)
\]
得到:
\[\nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \rho_\theta}[\nabla_\theta \log \rho_\theta(\tau) R(\tau)]
\]
展开 \(\log \rho_\theta(\tau)\):
\[\log \rho_\theta(\tau) = \log p_0(s_0) + \sum_{t=0}^T \log \pi_\theta(s_t,a_t) + \sum_{t=0}^T \log p(s_{t+1}|s_t,a_t)
\]
由于环境动态不依赖于 \(\theta\),梯度简化为:
\[\nabla_\theta \log \rho_\theta(\tau) = \sum_{t=0}^T \nabla_\theta \log \pi_\theta(s_t,a_t)
\]
因此:
\[\nabla_\theta J(\theta) = \mathbb{E}_{\tau \sim \rho_\theta}\left[\sum_{t=0}^T \nabla_\theta \log \pi_\theta(s_t,a_t) R(\tau)\right]
\]
REINFORCE 算法流程
-
使用当前策略 \(\pi_\theta\) 采样 \(N\) 条轨迹 \(\{\tau_i\}\);
-
计算每条轨迹的回报 \(R(\tau_i)\);
-
估计策略梯度:
\[\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=0}^T \nabla_\theta \log \pi_\theta(s_t,a_t) R(\tau_i)
\]
-
更新策略:
\[\theta \leftarrow \theta + \eta \nabla_\theta J(\theta)
\]
优点:
- 模型无关(model-free);
- 适用于部分可观测环境(POMDP)。
缺点:
- 高方差;
- 样本效率低;
- 只能用于回合式任务;
- 需频繁采样。
方差问题与基线校正
REINFORCE 的高方差源于:
- 策略与环境均为随机;
- 长时间跨度下,返回的不确定性积累。
解决方案之一是减去基线(baseline):
\[\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i,t} \nabla_\theta \log \pi_\theta(s_t,a_t) [R(\tau_i) - \hat{R}]
\]
其中:
\[\hat{R} = \frac{1}{N}\sum_i R(\tau_i)
\]
这种方式不会引入偏差(证明见 @Williams1992),但能有效降低方差与奖励尺度敏感性。
最优基线为:
\[b = \frac{\mathbb{E}[(\nabla_\theta \log \rho_\theta(\tau))^2 R(\tau)]}{\mathbb{E}[(\nabla_\theta \log \rho_\theta(\tau))^2]}
\]
在实践中,使用均值或状态值估计 \(\hat{V}(s_t)\) 即可。
策略梯度定理(Policy Gradient Theorem)
进一步推导得:
\[\nabla_\theta J(\theta) = \mathbb{E}_{s \sim \rho_\theta, a \sim \pi_\theta}[\nabla_\theta \log \pi_\theta(s,a) Q^{\pi_\theta}(s,a)]
\]
即:每个状态–动作的梯度加权其期望 Q 值。
这一定理的意义在于:
- 策略梯度可在单步转移上计算(可引入自举 bootstrapping);
- 允许与值函数近似器(critic)结合。
Actor–Critic 框架
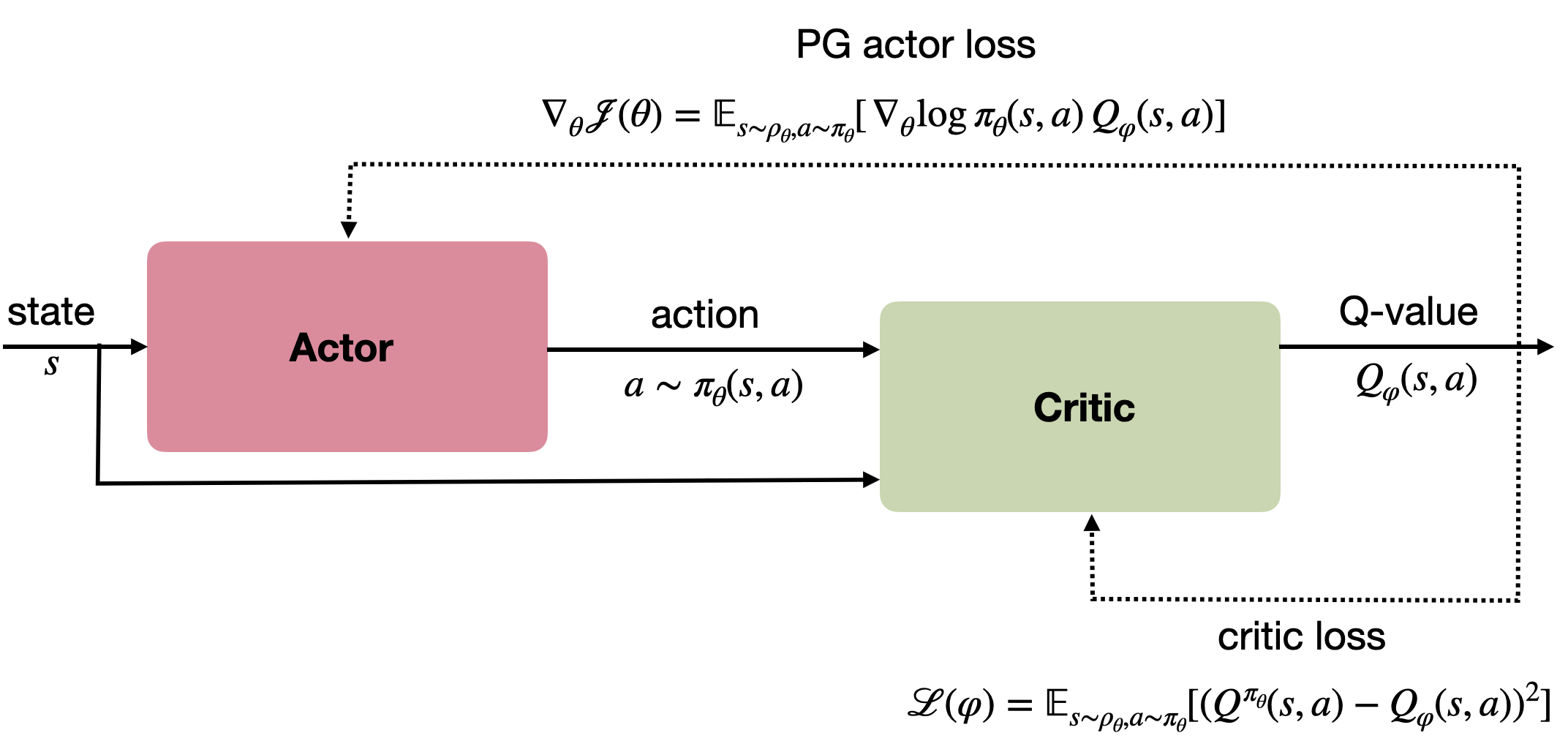
由策略梯度定理可得,策略学习可结合 Q 值估计形成 Actor–Critic 结构:
- Actor(行为者):学习策略 \(\pi_\theta(s,a)\);
- Critic(评论者):估计 Q 值 \(Q_\varphi(s,a)\)。
策略梯度:
\[\nabla_\theta J(\theta) = \mathbb{E}[\nabla_\theta \log \pi_\theta(s,a) Q_\varphi(s,a)]
\]
评论者的目标是最小化 TD 误差:
\[\mathcal{L}(\varphi) = \mathbb{E}[(r + \gamma Q_{\varphi'}(s',\arg\max_{a'} Q_\varphi(s',a')) - Q_\varphi(s,a))^2]
\]
![policygradient]()
该结构将策略梯度与时序差分学习结合,成为深度强化学习中最常用的框架之一。