我们知道,在 RS 锁存器中,输入信号由 11 变为 00 时,状态是不稳定的。能否利用这种不稳定性生成随机数?
事实上,前人早就想到了这个想法,并付诸实践,比如这篇论文。然而,网上鲜少有对相关内容的介绍。本文旨在概述论文的内容。
原理说来简单,但是为了让输出尽可能接近随机数,需要仔细设计电路的一些细节。影响随机性的因素有:
- 锁存器的内部不对称性;
- 芯片制造造成的不对称性;
- 来自电路其他部分的影响;
- 输入输出结点先前残留的电荷的影响。
仔细地布局电路,将锁存器对称地排布,可以消除内部不对称性;使用另一个锁存器,将原锁存器与电路的其他部分隔离开来;使用开关清除残留电荷。这样,除了芯片制造不可避免的公差以外,其余的问题均得到解决。电路图如下:
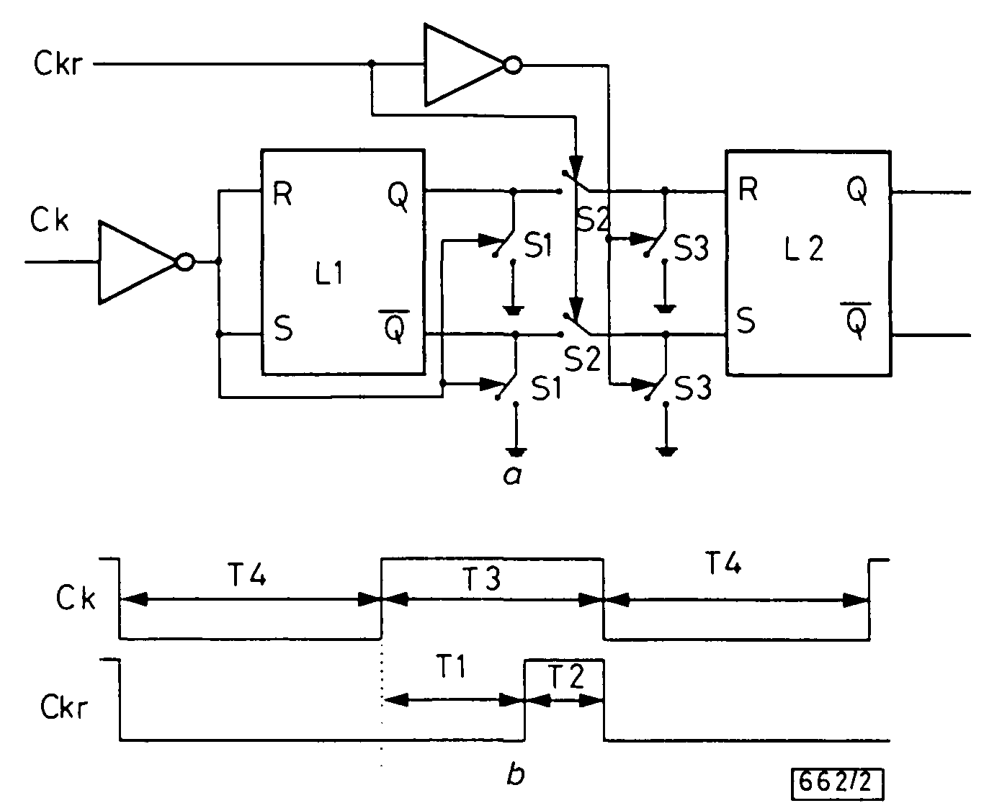
- 时间段 T4 中,开关 S1、S3 闭合,清除残留电荷;S2 断开,避免信号传播到后面。L1 的输入 \(R,S\) 均为 1,\(Q,\overline{Q}\) 均为 0。
- 时间段 T1 中,开关 S1、S2 断开,S3 闭合。L1 的输入 \(R,S\) 均为 0,开始震荡。在现实中,锁存器的震荡不可能一直持续,而是会存在一个“解决时间”(resolution time),表示震荡不会长于这个时间;我们要求 T1 大于解决时间,这样到下一个阶段开始时,L1 的输出已经稳定。
- 时间段 T2 中,开关 S1、S3 断开,S2 闭合。L1 的最终输出传递给 L2,这样生成的随机数就被锁存在 L2 中。
为了减小相邻数字之间的相关性,还可以每若干个输出取样一次,并舍弃其余的数。论文中测试的结果是:每 4 个数取样一次,就可以通过大部分的随机性检测。
