缺失数据处理一直是机器学习实践中的难点。MICE(Multivariate Imputation by Chained Equations)作为一种基于迭代思想的插补框架,可以处理复杂缺失值问题。因为它不是简单地用均值或中位数填补空缺,而是通过构建后验分布来建模不确定性,这种处理方式在统计学上更为严谨。
但MICE的学习曲线优点陡峭,迭代机制和模型依赖特性也让不少人望而却步,所以本文会通过PMM(Predictive Mean Matching)和线性回归等具体方法,拆解MICE的工作原理,同时对比标准回归插补作为参照。
MICE的基本概念
插补方法大致可以分三类:统计方法(均值、中位数、众数)、基于模型的方法(KNN、回归插补、GAIN等)、以及时间序列特有的前向后向填充。MICE属于模型方法,但它的实现路径更复杂——通过迭代式预测来逐步逼近真实分布。
整个流程如下图所示: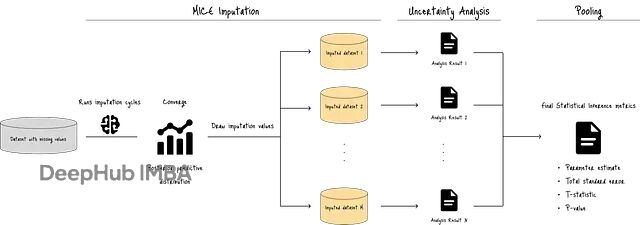
MICE首先运行多轮插补循环,用预测模型生成目标变量的后验分布。接着从这个分布中反复抽样(比如M次),生成多个版本的完整数据集。每个数据集的插补值都不相同,这种变异性是MICE的核心价值所在。
最后通过不确定性分析和池化(pooling),得到汇总的统计指标:池化参数估计、总标准误差、t统计量和p值。这些指标量化了缺失值带来的不确定性,帮助判断插补结果是否足够可靠。
https://avoid.overfit.cn/post/e54f988c93df418db5ccbd1d37a92007
