我们可能都听说过傅里叶级数,但我们确切地知道它是什么吗?在这篇文章中,我将尝试逐一剖析这些概念。希望到最后,当你听到这些术语时,无论是在机器学习文献中还是与数学相关的内容中,你都能明白是怎么回事。
傅里叶级数是由巴蒂斯特·约瑟夫·傅里叶男爵在19世纪初引入的,傅里叶向我们展示了任何周期函数都可以表示为一系列正弦和余弦。这种表示被称为傅里叶级数。
现在,给定一个周期函数 \(y=f(t)\),使用傅里叶级数,我们希望将其表示为以下形式的正弦和余弦的无限和:
\[f(t) \approx a_0 + a_1\cos(t) + a_2\cos(2t) + a_3\cos(3t) + ... + a_n\cos(nt) \\
+ b_1\sin(t) + b_2\sin(2t) + b_3\sin(3t) + ... + b_n\sin(nt)
\]
在这里,\(a_{0,..,n}\) 和 \(b_{0,..,n}\) 是系数,\(a_0\) 项有助于将图形垂直上下移动。不断将这些加权项加在一起,其近似值就越接近原始函数 \(f(t)\)。
这个傅里叶级数可以分解成两个部分:傅里叶正弦和余弦级数。
傅里叶正弦级数
现在,让我们放大级数的sin分量。所有与sin相关的项的总和构成了傅里叶正弦级数。
对于一个奇函数 \(f(x)\),
\[f(x) \approx \sum_{n=1}^{\infty} b_n \sin(nt)
\]
假设我们在 \([-\pi, \pi]\) 中有一个方波函数 \(SW(t)\):
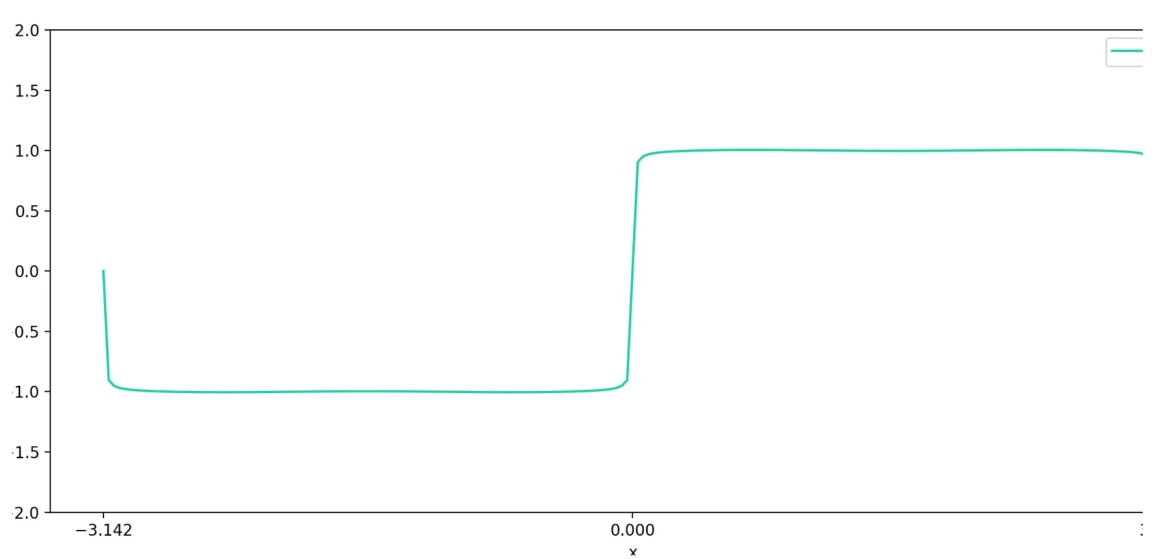
如果我们将 \(\sin(t)\) 的图形叠加到这个图形上,它会看起来像这样:
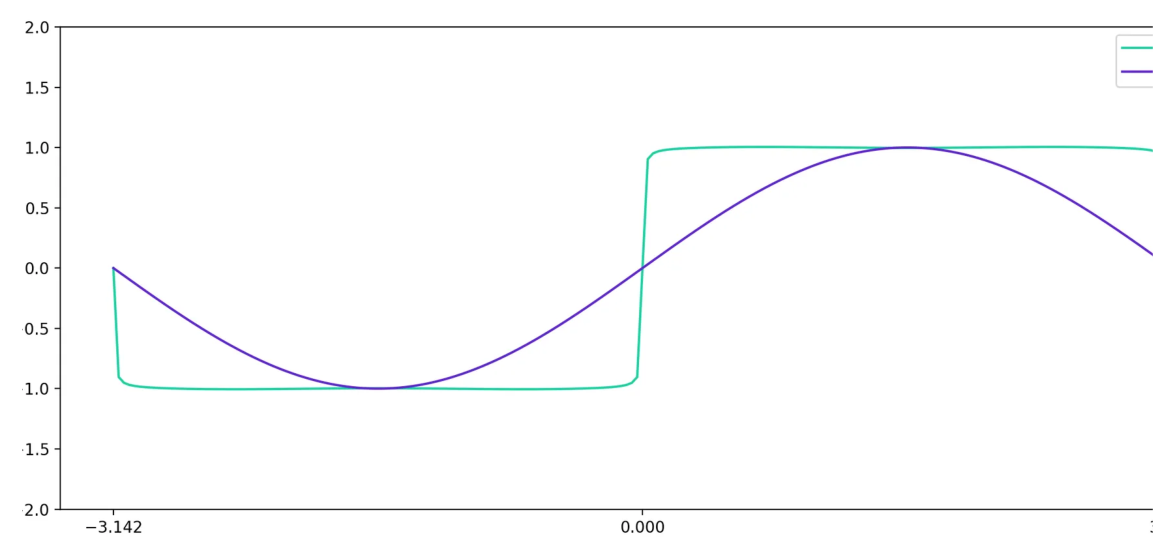
现在,让我们叠加 \(y = \frac{\sin(3t)}{3}\) 的图形。
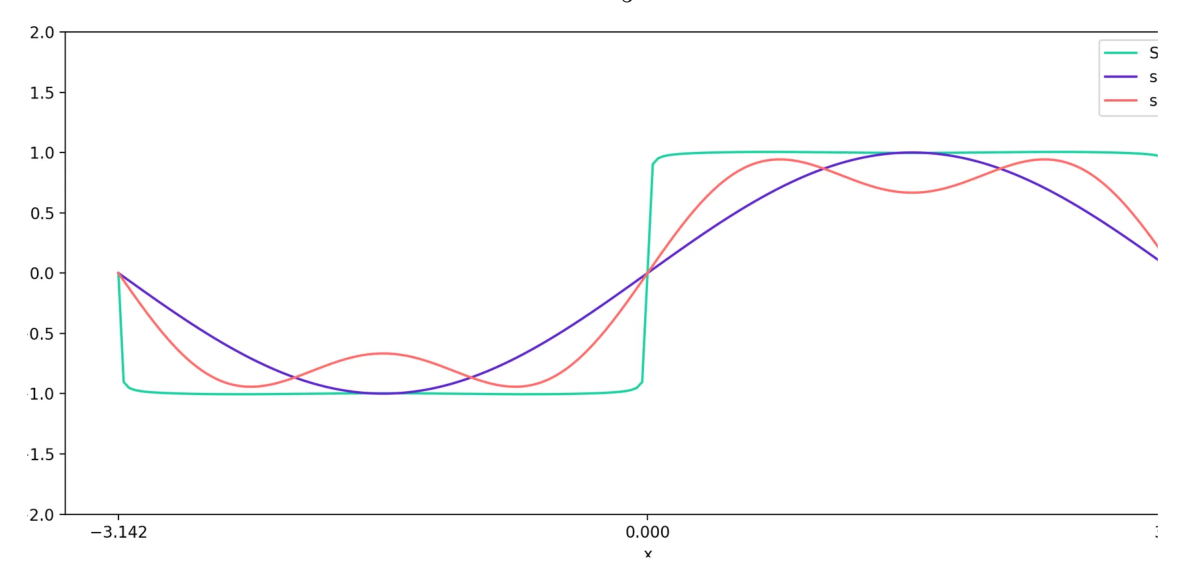
当我们把这两个图形,\(y = \sin(t)\) 和 \(y = \frac{\sin(3t)}{3}\),加在一起,我们得到一个新的曲线 \(y = \sin(t) + \frac{\sin(3t)}{3}\)。
现在,如果我们将 \(y = \frac{\sin(5t)}{5}\) 添加到这个紫色曲线上,我们会得到一些更不同(但更接近方波)的东西。
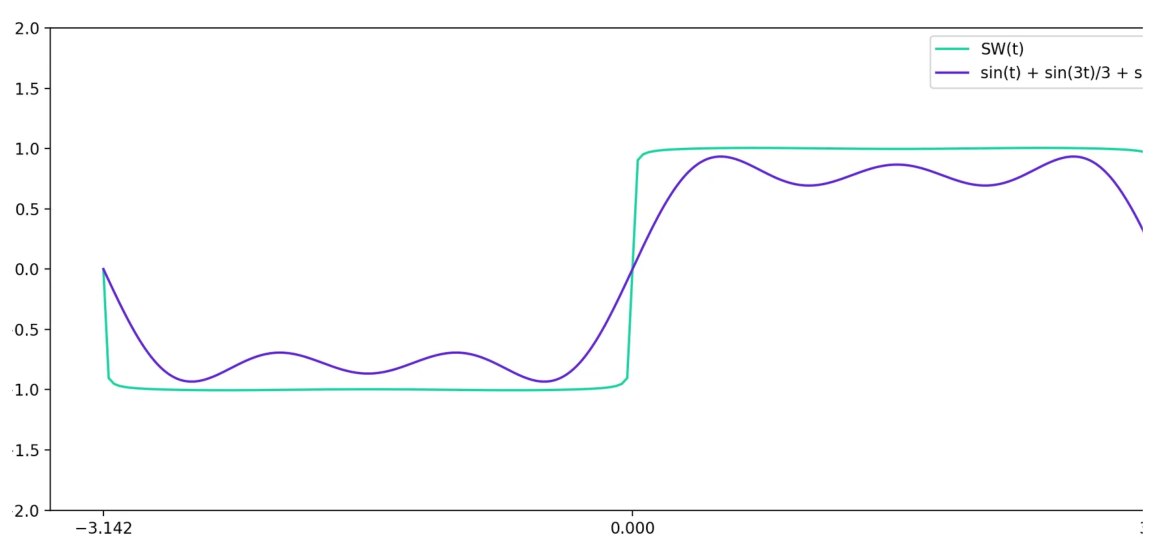
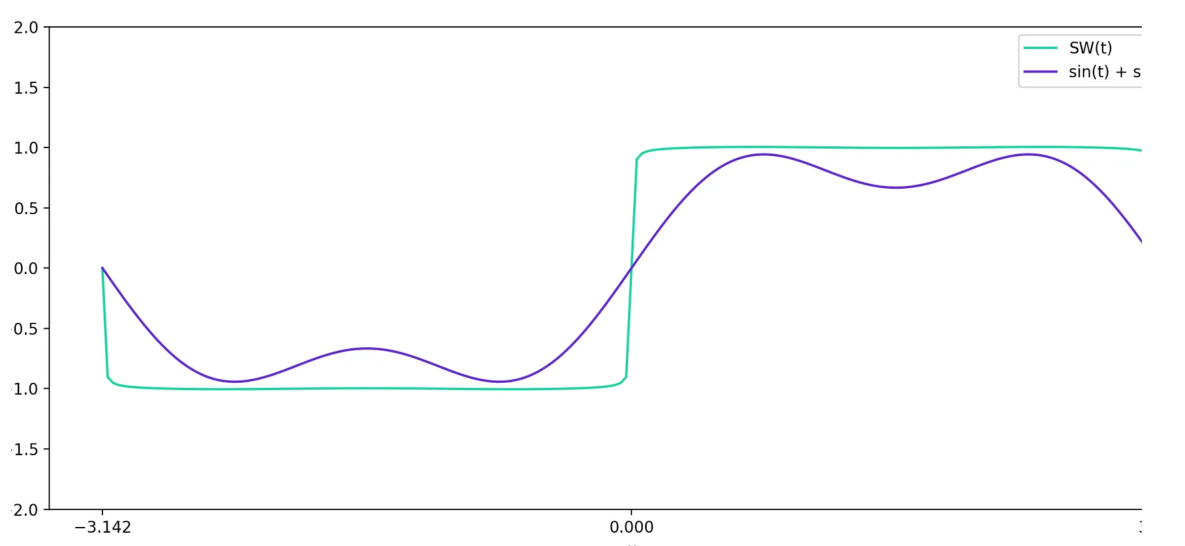
继续这样做,直到达到 \(\frac{\sin(199t)}{199}\) 项。就像这样,
\[y = \sin(t) + \frac{\sin(3t)}{3} + \frac{\sin(5t)}{5} + ... + \frac{\sin(197t)}{197} + \frac{\sin(199t)}{199}
\]
我们会得到这样的东西:
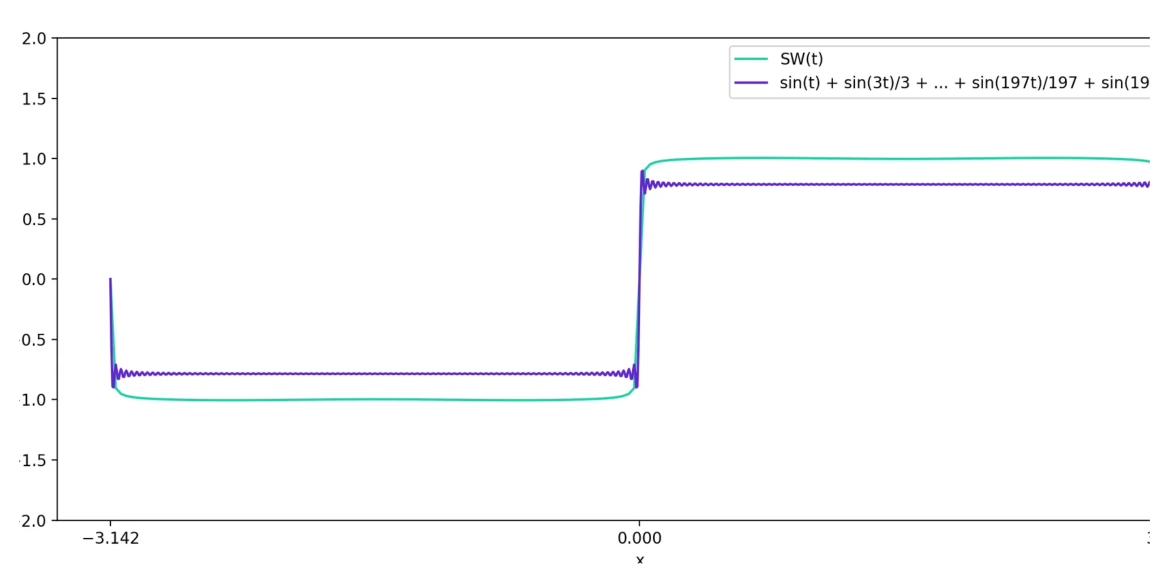
所以,可以通过添加傅里叶正弦级数的项,近似任何形状类似于正弦波的奇周期函数。
傅里叶余弦级数
同样适用于余弦波,可以使用傅里叶余弦级数中的项的总和来近似偶周期函数的图形:
\[f(x) \approx a_0 + \sum_{n=1}^{\infty} a_n \cos(\frac{nx}{2})
\]
即任何周期函数都可以用sin和cos项的和来表示/近似。对于偶函数,它是cos项的和,对于奇函数,它是sin项的和。
首要任务是找到这些系数 \(a_0, a_1, a_2, ..., a_n\) 和 \(b_1, b_2, ..., b_n\) 的确切值。为此,我们可以对每一项使用定积分。傅里叶通过将其简化为以下公式来计算这些系数:
\[a_0 = \frac{1}{2\pi} \int_0^{2\pi} f(t) dt
\]
\[a_n = \frac{1}{\pi} \int_0^{2\pi} f(t) \cos(nt) dt
\]
\[b_n = \frac{1}{\pi} \int_0^{2\pi} f(t) \sin(nt) dt
\]
傅里叶是如何得出这些积分的呢?
我们可以将 \(f(t)\) 的傅里叶展开表示为:
\[f(t) \approx a_0 + \sum_{n=1}^{\infty} a_n \cos(nt) + \sum_{n=1}^{\infty} b_n \sin(nt)
\]
如果我们像泰勒级数或麦克劳林级数那样对它进行微分,我们会得到 \(a_0\) 为零,并且会得到交替的\(\sin,\cos\),这违背了微分的目的,因为我们仍然无法得到值。所以,傅里叶尝试了积分:
\[\int_{-\pi}^{\pi} f(t) dt \approx \int_{-\pi}^{\pi} a_0 dt + \int_{-\pi}^{\pi} \sum_{n=1}^{\infty} a_n \cos(nt) dt + \int_{-\pi}^{\pi} \sum_{n=1}^{\infty} b_n \sin(nt) dt
\]
寻找 \(a_0\)
上面的表达式可以重写为
\[\int_{-\pi}^{\pi} f(t) dt \approx \int_{-\pi}^{\pi} a_0 dt + \sum_{n=1}^{\infty} \int_{-\pi}^{\pi} a_n \cos(nt) dt + \sum_{n=1}^{\infty} \int_{-\pi}^{\pi} b_n \sin(nt) dt
\]
在 \([-\pi, \pi]\) 中,\(\displaystyle\int_{-\pi}^{\pi} a_0 dt\) 简化为 \(2\pi a_0\)。对于 \(\sin\) 和 \(\cos\) 项,
\[\int_{-\pi}^{\pi} \cos(nt) dt = \frac{1}{n} [\sin(nt)]_{-\pi}^{\pi} = 0
\]
这意味着整个求和 \(\displaystyle\sum_{n=1}^{\infty} \int_{-\pi}^{\pi} a_n \cos(nt)\) 不复存在,因为它归零了。
\[\int_{-\pi}^{\pi} \sin(nt) dt = -\frac{1}{n} [\cos(nt)]_{-\pi}^{\pi} = 0
\]
我们可以看到求和 \(\displaystyle\sum_{n=1}^{\infty} \int_{-\pi}^{\pi} b_n \sin(nt)\) 也归零了。所以
\[\int_{-\pi}^{\pi} f(t) dt = 2\pi a_0 + 0 + 0
\]
两边都除以 \(2\pi\)
\[a_0 = \frac{1}{2\pi} \int_{-\pi}^{\pi} f(t) dt
\]
将区间更改为 \([0, 2\pi]\)
\[a_0 = \frac{1}{2\pi} \int_0^{2\pi} f(t) dt
\]
寻找 \(a_n\)
让我们回到原始方程:
\[\int_{-\pi}^{\pi} f(t) dt \approx \int_{-\pi}^{\pi} a_0 dt + \sum_{n=1}^{\infty} \int_{-\pi}^{\pi} a_n \cos(nt) dt + \sum_{n=1}^{\infty} \int_{-\pi}^{\pi} b_n \sin(nt) dt
\]
我们需要在这个方程中加入其他东西来帮助我们。它到底是什么?
是 \(\cos(mt)\),其中 \(m \in \mathbb{Z}\)!我们需要将方程的两边都乘以这个项:
\[\int_{-\pi}^{\pi} f(t)\cos(mt) dt \approx \int_{-\pi}^{\pi} a_0 \cos(mt) dt + \sum_{n=1}^{\infty} \int_{-\pi}^{\pi} a_n \cos(nt)\cos(mt) dt + \sum_{n=1}^{\infty} \int_{-\pi}^{\pi} b_n \sin(nt)\cos(mt) dt
\]
- 让我们从看一下 \(\displaystyle\int_{-\pi}^{\pi} a_0 \cos(mt) dt\) 开始。这和我们之前做的一样,值为 \(0\),我们不需要再关心它了。
- 接下来,我们转到 \(\displaystyle\sum_{n=1}^{\infty} \int_{-\pi}^{\pi} a_n \cos(nt)\cos(mt) dt\)。使用简单的积和恒等式,我们可以将其简化为以下两种情况:
\[\sum_{n=1}^{\infty} \int_{-\pi}^{\pi} \cos(nt)\cos(mt) dt = \begin{cases} 0 & n \neq m \\ \pi & n=m \end{cases}
\]
所以,当 \(n=m\) 时,\(\displaystyle\sum_{n=1}^{\infty} \int_{-\pi}^{\pi} a_n \cos(nt)\cos(mt) dt\) 简化为 \(a_n \pi\)。
- 接下来,我们转到 \(\displaystyle\sum_{n=1}^{\infty} \int_{-\pi}^{\pi} b_n \sin(nt)\cos(mt) dt\):
\[\sum_{n=1}^{\infty} \int_{-\pi}^{\pi} \sin(nt)\cos(mt) dt = 0
\]
\[\int_{-\pi}^{\pi} f(t)\cos(mt) dt = 0 + a_n\pi + 0
\]
两边都除以 \(\pi\) 并将 \(m\) 改为 \(n\)
\[a_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(t)\cos(nt) dt
\]
将区间更改为 \([0, 2\pi]\)
\[a_n = \frac{1}{\pi} \int_0^{2\pi} f(t)\cos(nt) dt
\]
寻找 \(b_n\)
最后,让我们来寻找 \(b_n\)。如果你说我们现在将在两边都乘以 \(\sin(mt)\),那你就猜对了。
\[\int_{-\pi}^{\pi} f(t)\sin(mt) dt \approx \int_{-\pi}^{\pi} a_0 \sin(mt) dt + \sum_{n=1}^{\infty} \int_{-\pi}^{\pi} a_n \cos(nt)\sin(mt) dt + \sum_{n=1}^{\infty} \int_{-\pi}^{\pi} b_n \sin(nt)\sin(mt) dt
\]
- 和以前一样,\(\displaystyle\int_{-\pi}^{\pi} a_0 \sin(mt) dt = 0\)。
- 考虑 \(\displaystyle\sum_{n=1}^{\infty} \int_{-\pi}^{\pi} a_n \cos(nt)\sin(mt) dt\):
\[\sum_{n=1}^{\infty} \int_{-\pi}^{\pi} \cos(nt)\sin(mt) dt = 0
\]
所以
\[\sum_{n=1}^{\infty} \int_{-\pi}^{\pi} a_n \cos(nt)\sin(mt) dt = 0
\]
- 最后考虑 \(\displaystyle\sum_{n=1}^{\infty} \int_{-\pi}^{\pi} b_n \sin(nt)\sin(mt) dt\)。注意到
\[\sum_{n=1}^{\infty} \int_{-\pi}^{\pi} \sin(nt)\sin(mt) dt = \begin{cases} 0 & n \neq m \\ \pi & n=m \end{cases}
\]
同样地,\(\displaystyle\sum_{n=1}^{\infty} \int_{-\pi}^{\pi} b_n \sin(nt)\sin(mt) dt = b_n \pi\).
\[\int_{-\pi}^{\pi} f(t)\sin(mt) dt = 0 + 0 + b_n\pi
\]
两边都除以 \(\pi\) 并将 \(m\) 改为 \(n\)
\[b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(t)\sin(nt) dt
\]
将区间更改为 \([0, 2\pi]\)
\[b_n = \frac{1}{\pi} \int_0^{2\pi} f(t)\sin(nt) dt
\]






