题意:有一个数轴, \(Q\) 次操作,三种操作类型:
- 1.在位置为 \(x\) 处插入权值为 \(w\) 的数,不会在有数的位置重复插入。
- 2.删除位置 \(x\) 处的数,保证删前 \(x\) 处有数。
- 3.给定位置 \(x\) ,对于一个数轴上有数的位置 \(y\) ,定义其价值为 \(\frac{w_y}{|y-x|}\) ,查询最大价值。
先假设没有修改操作。
对于一个查询 \(x\) ,我们可以分开处理小于 \(x\) 的位置和大于 \(x\) 的位置。不妨先考虑大于 \(x\) 的位置。把每一个数看作是二维平面上的一个点,一个点能成为哪些位置的最优选择?
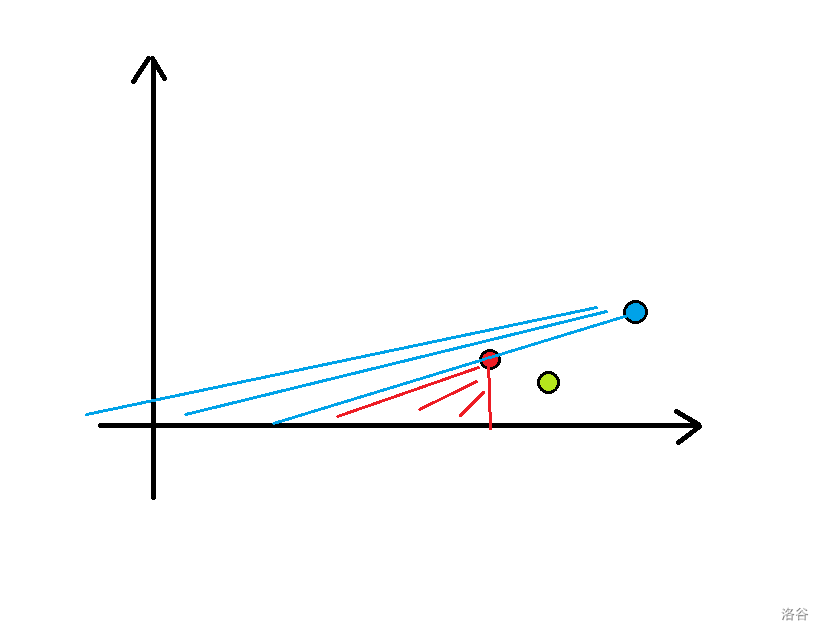
如图,对应颜色的线条为该点所能影响的区域。我们可以维护一个凸包。
加上修改,可以考虑线段树分治,对于操作时间建立线段树,统计每一个修改和查询对应的时刻区间。对于每个线段树上的节点维护一个凸包,本题求的是区间max,两个时间区间的答案可以直接合并。
按在数轴上的位置将插入和查询从右到左排序,依次在线段树上插入和查询。
对于在查询左边的情况也是类似的
