《电路基础》第五章学习笔记
本章主要介绍运算放大器。
一个特性与电压控制电压源类似的电子元件。可以对信号进行相加、放大、积分和微分。可以看作增益非常高的电压放大器。
-
运算放大器
-
定义:
运算放大器是一个用于执行加、减、乘、出、微分与积分等数学运算的有源电路器件。
它是由电阻、晶体管、电容和二极管等构成的复杂有源电路元件。
-
封装:
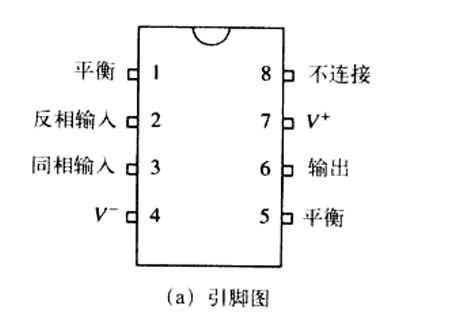
运放的封装是典型的8引脚双列直插封装(DIP)
一般来说,引脚8是不用的,引脚1,5一般不外接元件。
5个重要的引脚分别是:
- 反相输入端,引脚2
- 同相输入端,引脚3
- 输出端,引脚6
- 正电源端V’,引脚7
- 负电源端V,引脚4
-
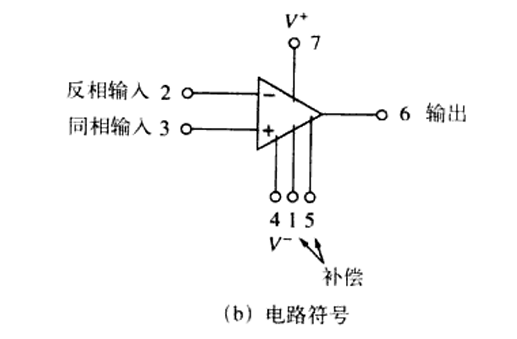
封装,电路符号,实物图

-
等效电路模型:

上图是运放的等效电路模型,我们可以使用戴维南分析,乘以增益A之后,得到:
\[v_{o}=Av_{d}=A(v_{2}-v_{1}) \]其中A为开环电压增益。
-
反馈:
当输出反馈至运算放大器的反相输入端时,即构成负反馈
如果存在输出电压与输入电压之比则称为闭环增益
运算放大器总是用于带反馈的电路中。
-
限制:
输出电压不能超过|\(V_{CC}\)|。
运放的输出电压取决于并受限于电源电压。
函数关系如下:

-
注意:
虽然我们总是在线性区应用运算放大器,但在设计运算放大器电路时,仍然要注意其可能进入饱和状态,以避免所设计的运放在实验中不能正常工作。
-
-
反相放大器
-
特点:
输入信号与反馈信号都作用在运放的反相输入端上。

电压增益为
\[A_{v}=\frac{v_{0}}{v_{i}}=-\frac{R_{f}}{R_{1}} \]正是因为最后的负号,所以命名为“反相”放大器。
-
-
同相放大器
-
特点:
同相放大器是提供正电压增益的运放电路。
它的输出与输入具有相同的极性

我们用KCL得出:
\[v_{o}=(1+\frac{R_{f}}{R_{1}})v_{i} \]增益A:
\[A_{v}=\frac{v_{0}}{v_{i}}=1+\frac{R_{f}}{R_{1}} \]
-
-
加法放大器
-
特点:
加法放大器是将若干个输入合并,并且在输出端产生这些输入的加权和的运算放大器。

如上图,出现了\(R_{1}\)、\(R_{2}\)、\(R_{3}\)的并联电路。
这就起到了加法电路的作用!
对节点a应用KCL,同时考虑流入运放各个输入端的电流为0。
化简得到:
\[v_{o}=-(\frac{R_{f}}{R_{1}}v_{1}{\color{red} +} \frac{R_{f}}{R_{2}}v_{2}{\color{red} +} \frac{R_{f}}{R_{3}}v_{3}) \]我们可以发现,输出电压为各个输入电压的加权和,因此将上图电路称为加法器。
加法器可以有三个以上的输入。
-
-
差分放大器(减法器)
-
特点:
差分放大器是放大两个输入信号之差,从而抑制两个输入的共模信号的器件。
这个分析起来有点复杂啊!
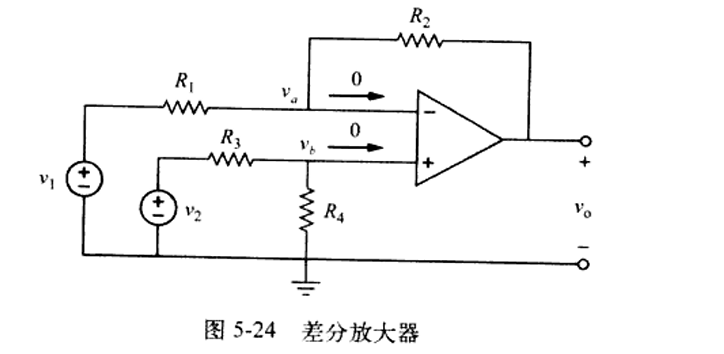
如上图,求出\(v_{0}\)要在a,b点分别列KCL。
化简可得:
\[v_{o}=(\frac{R_{1}}{R_{2}}+1)\frac{R_{4}}{R_{3}+R_{4}}v_{2}-\frac{R_{2}}{R_{1}}v_{1} \] 当\(v_{1}\)=\(v_{2}\)时,\(v_{o}\)=0,所以当:
\[\frac{R_{1}}{R_{2}}=\frac{R_{3}}{R_{4}} \] 上式变为:
-
更进一步:当\(R_{1}=R_{2}\)或\(R_{3}=R_{4}\)时,输出为:
-
级联运算放大器电路
-
级联:
两个或多个运算放大器电路首尾顺序相连,使得前者的输出为下一级的输入。

级联总增益为各个运放电路增益的乘积。
-
运放这一章还有12页课后习题,国庆假期慢慢写吧,有点多!
