你在 \(0\) 时刻位于数轴上的 \(0\) 位置。每个时刻开始时,你可以选择右移一个单位,或者停在原地。在第 \(t\) 个时刻结束时,如果你的位置 \(p\) 满足 \(p \equiv b_{t\bmod n} \pmod {a_{t\bmod n}}\),那么你就输了,注意 \(0\) 时刻可能已经满足这个条件,但是忽略这种情况。
询问到达数轴上 \(m\) 位置需要的最少时间,或报告不可能。
\[1\le n,a_i \le 10,1\le m \le 10^{12}
\]
敏锐地注意到数据范围非常小。
首先一个观察是,能向前走的时候就向前走一定是最优的。
证明是,假设某一个时刻等待能够比向前走更快达到终点,
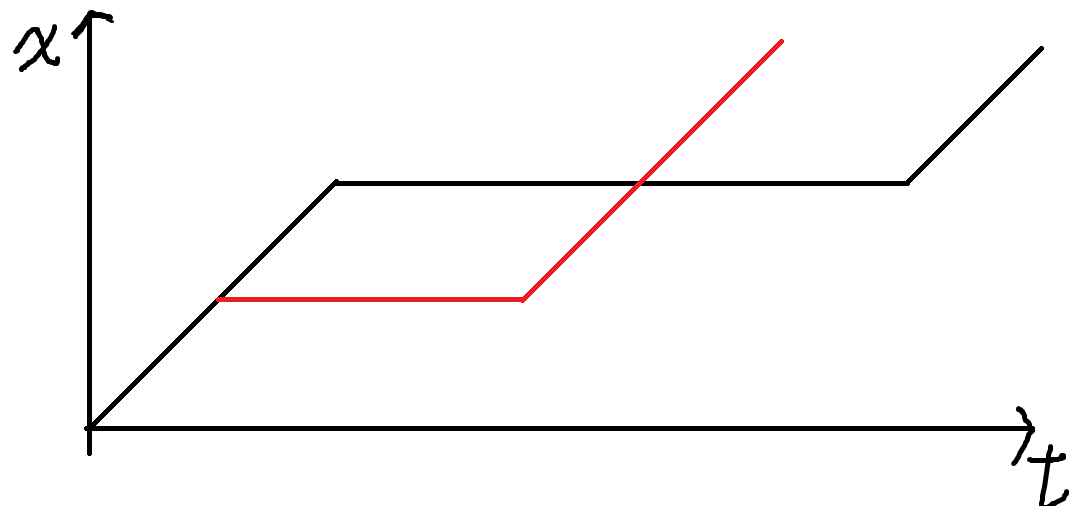
那么我们调整成如图的绿色路线一定不会更劣。
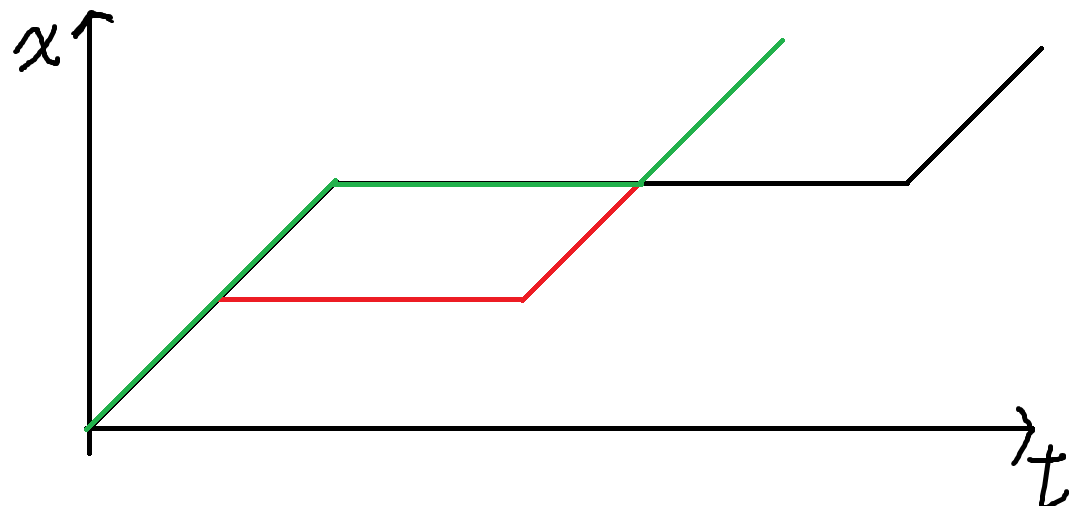
因此我们只需要贪心地向前走就可以了。
考虑加速这个过程。
发现 \(\text{LCM}(1,2,3,4,5,6,7,8,9,10)=2520\)。
因此我们可以记录 \(f_{i,j,k}\),表示当前状态满足 \(t\equiv i\pmod n\),\(p\equiv j\pmod {LCM}\),经过 \(2^k\) 时间后,能走多远。
边界状态是 \(f_{i,j,0}=[j+1\not\equiv b_{(i+1)\bmod n} \pmod {a_{(i+1)\bmod n}}]\)。
然后可以简单递推,查询的时候倍增即可。
#pragma GCC optimize("Ofast", "inline")
#include <algorithm>
#include <iostream>
#include <vector>
#include <tuple>const int N = 11, M = 60, L = 2521;
#define rep(i,a,b) for(int i(a);i<=(b);++i)
#define rap(i,a,b) for(int i(a);i<(b);++i)
typedef long long i64;i64 m;
int n;
int a[N], b[N], pow2[M];
i64 dp[M][N][L];
void solve() {std::cin >> n >> m; int L = 1;rep(i, 1, n) std::cin >> a[i], L = L * a[i] / std::__gcd(L, a[i]);rep(i, 1, n) std::cin >> b[i];a[0] = a[n], b[0] = b[n], pow2[0] = 1;rap(i, 1, M) pow2[i] = pow2[i-1] * 2 %n;rap(i, 0, n) {rap(j, 0, L) {int x = (i + 1) % n;dp[0][i][j] = (j + 1) % a[x] != b[x];}}i64 turn = 1;rap(k, 1, M) {rap(i, 0, n) {rap(j, 0, L) {int a = (i + turn) % n, b = (j + dp[k-1][i][j]) % L;dp[k][i][j] = dp[k-1][i][j] + dp[k-1][a][b];}} turn = turn * 2 %n;}i64 last = m, ans = 0;int a = 0, b = 0;for(int i = M - 1; i >= 0; --i) {if(last > dp[i][a][b]) {last -= dp[i][a][b];b = (b + dp[i][a][b]) %L;a = (a + pow2[i]) %n;ans += 1ll << i;}}for(int i = M - 1; i >= 0; --i) {if(dp[i][a][b] == 0) {b = (b + dp[i][a][b]) %L;a = (a + pow2[i]) %n;ans += 1ll << i;}}if(dp[0][a][b] == 0) std::cout << "-1\n";else std::cout << ans+1 << "\n";
}int main() {std::ios::sync_with_stdio(0), std::cin.tie(0), std::cout.tie(0);int t; std::cin >> t; for(; t--; ) solve();
}
