为什么需要 Huffman 编码?—— 从 “编码浪费” 说起
在数据通信或存储中,我们需要将字符转换成二进制码(如 ASCII 码)。但常规编码(如 ASCII)存在一个问题:无论字符出现频率高低,都用相同长度的编码(比如 ASCII 码每个字符 8 位),这会造成大量空间 / 带宽浪费。
举个例子:要传输字符串 “ABABBCBBA”(共 9 个字符)
- 若用 ASCII 码:A (01000001)、B (01000010)、C (01000011),每个字符 8 位,总长度 = 9×8=72 位;
- 观察发现:B 出现 5 次(高频)、A 出现 3 次(中频)、C 出现 1 次(低频)。如果让高频字符用短码、低频字符用长码,就能大幅缩减总长度。
比如给 B 分配 1 位码 “0”、A 分配 2 位码 “10”、C 分配 2 位码 “11”,总长度 = 5×1 + 3×2 + 1×2 = 5+6+2=13 位,仅为 ASCII 码的 1/5 左右!
这种 “按频率分配编码长度” 的思路,就是 Huffman 编码的核心 ——用最少的二进制位实现无歧义的字符编码,解决 “编码浪费” 问题。
Huffman 编码的关键原则
Huffman 编码能实现 “无歧义” 和 “高效压缩”,依赖两个核心原则:
- 高频短码、低频长码:频率越高的字符,编码长度越短,最大化压缩效果;
- 前缀编码特性:任何一个字符的编码,都不是另一个字符编码的 “前缀”(比如 A=10、B=0、C=11,没有编码是其他编码的开头),确保译码时不会出现二义性。
比如若 A=1、B=10,那么遇到 “10” 时,无法判断是 “B” 还是 “A+0”,这就是非前缀编码的问题;而 Huffman 编码通过 “二叉树路径” 天然保证前缀特性。
Huffman 树 —— 实现 Huffman 编码的核心结构
Huffman 编码的本质是 “一棵特殊的二叉树(Huffman 树)的路径编码”。要理解 Huffman 编码,必须先掌握 Huffman 树的概念和构建方法。
Huffman 树的基本概念
先明确 3 个关键定义(后续计算和构建都依赖这些概念):
- 权(Weight):给节点赋予的数值,在 Huffman 编码中,“权” 就是字符的出现频率(如 A 的权 = 3、B 的权 = 5);
- 路径与路径长度:从根节点到某一叶子节点的 “边的数量” 就是路径长度。比如根→左子树→叶子,路径长度 = 2;
- 带权路径长度(WPL):叶子节点的 “权 × 该节点的路径长度”,整棵树的 WPL 是所有叶子节点的带权路径长度之和。
Huffman 树的核心定义:给定 n 个带权叶子节点,能使整棵树 WPL 最小的二叉树,称为 Huffman 树(最优二叉树)。
直观理解:为什么 Huffman 树的 WPL 最小?
用例子对比:3 个叶子节点,权值分别为 1(C)、3(A)、5(B),两种二叉树结构的 WPL 差异:

- WPL = (1∗2+2∗6)+(1∗2+2∗8+3∗1)+(1∗5)=14+21+5=41。
结构 2(Huffman 树,最优):
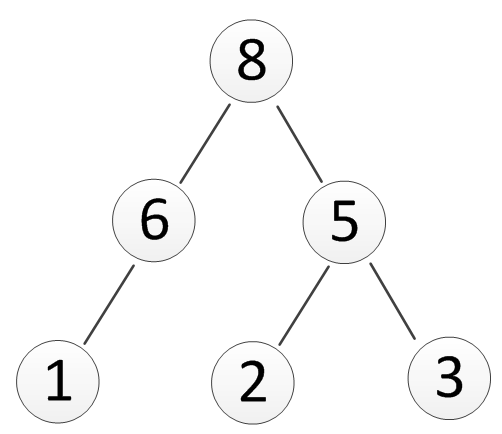
- WPL = (1∗6+2∗1)+(1∗5+2∗2)+(1∗5+2∗3)=8+9+11=28(更小)。
结论:Huffman 树通过 “让权值大的叶子离根更近”,最小化总 WPL,这和 “高频字符用短码” 的需求完全匹配!
Huffman 树的节点数量推导
构建 Huffman 树前,需知道树的总节点数,方便分配存储空间。推导基于 “二叉树的度与节点数关系”:
关键概念:节点的 “度”
- 度为 0 的节点(n₀):叶子节点(Huffman 树中就是带权的字符节点,如 A、B、C);
- 度为 1 的节点(n₁):只有一个子节点的节点;
- 度为 2 的节点(n₂):有两个子节点的节点(Huffman 树中合并生成的节点都是度为 2)。
推导过程:
- 二叉树总节点数公式:
n = n₀ + n₁ + n₂(总节点 = 叶子 + 度 1 + 度 2 节点); - 二叉树边数关系:树的边数 = 总节点数 - 1(比如 3 个节点有 2 条边);同时,边数也等于 “度 1 节点数 ×1 + 度 2 节点数 ×2”(每个度 1 节点贡献 1 条边,度 2 贡献 2 条),即
n-1 = n₁ + 2n₂; - 联立两个公式:
n₀ + n₁ + n₂ - 1 = n₁ + 2n₂→ 化简得n₂ = n₀ - 1(度 2 节点数 = 叶子数 - 1); - Huffman 树的特殊性质:没有度为 1 的节点(n₁=0)(因为每次合并都是选两个节点,生成的新节点一定有两个子节点,不会出现单个子节点的情况);
- 最终总节点数:
n = n₀ + 0 + (n₀ - 1) = 2n₀ - 1。 - 例子:“ABABBCBBA” 有 3 个叶子节点(n₀=3),所以 Huffman 树总节点数 = 2×3-1=5,和后续构建结果一致。
Huffman 树的构建步骤(以 “ABABBCBBA” 为例)
构建 Huffman 树的核心逻辑:反复合并两个权值最小的节点,直到只剩一个根节点。具体步骤如下:
步骤 1:统计字符频次(确定叶子节点)
先统计字符串中每个字符的出现次数(即 “权值”):
- A:出现 3 次 → 权 = 3;
- B:出现 5 次 → 权 = 5;
- C:出现 1 次 → 权 = 1;得到 n₀=3 个叶子节点:(A,3)、(B,5)、(C,1)。
步骤 2:初始化 Huffman 树数组
根据总节点数 = 2n₀-1=5,创建一个数组存储 Huffman 树节点。每个节点需包含以下信息(用结构体表示):
typedef struct {char ch; // 字符(仅叶子节点有值,合并节点为'\0')int weight; // 权值(字符频次或合并后的总权值)int parent; // 父节点在数组中的索引(0表示无父节点)int lchild; // 左子节点索引(0表示无子节点)int rchild; // 右子节点索引
} HuffmanNode;
初始化后,数组前 3 个元素为叶子节点,后 2 个为待合并的空节点:
| 索引 | ch | weight | parent | lchild | rchild |
|---|---|---|---|---|---|
| 0 | 'A' | 3 | 0 | 0 | 0 |
| 1 | 'B' | 5 | 0 | 0 | 0 |
| 2 | 'C' | 1 | 0 | 0 | 0 |
| 3 | '\0' | 0 | 0 | 0 | 0 |
| 4 | '\0' | 0 | 0 | 0 | 0 |
步骤 3:循环合并最小权值节点
核心操作:每次从 “无父节点” 的节点中,选两个权值最小的节点,合并成一个新节点(权值 = 两节点权值之和),并更新父、子节点索引。
第一次合并(生成索引 3 的节点):
- 无父节点的节点:0 (A,3)、1 (B,5)、2 (C,1);
- 选权值最小的两个:2 (C,1)、0 (A,3);
- 新节点(索引 3):weight=1+3=4,lchild=2(权小的作为左子节点),rchild=0,parent=0;
- 更新子节点父索引:A (0) 的 parent=3,C (2) 的 parent=3。此时数组状态:
| 索引 | ch(字符) | weight(权值 / 频次) | parent(父节点索引) | lchild(左子节点索引) | rchild(右子节点索引) |
|---|---|---|---|---|---|
| 0 | 'A' | 3 | 3 | 0 | 0 |
| 1 | 'B' | 5 | 0 | 0 | 0 |
| 2 | 'C' | 1 | 3 | 0 | 0 |
| 3 | '\0' | 4 | 0 | 2 | 0 |
| 4 | '\0' | 0 | 0 | 0 | 0 |
第二次合并(生成索引 4 的根节点):
- 无父节点的节点:1 (B,5)、3 (4);
- 选权值最小的两个:3 (4)、1 (B,5);
- 新节点(索引 4,根节点):weight=4+5=9,lchild=3,rchild=1,parent=0;
- 更新子节点父索引:3 的 parent=4,B (1) 的 parent=4。最终 Huffman 树数组(构建完成):
| 索引 | ch(字符) | weight(权值 / 频次) | parent(父节点索引) | lchild(左子节点索引) | rchild(右子节点索引) |
|---|---|---|---|---|---|
| 0 | 'A' | 3 | 3 | 0 | 0 |
| 1 | 'B' | 5 | 4 | 0 | 0 |
| 2 | 'C' | 1 | 3 | 0 | 0 |
| 3 | '\0' | 4 | 4 | 2 | 0 |
| 4 | '\0' | 9 | 0 | 3 | 1 |
步骤 4:最终 Huffman 树结构
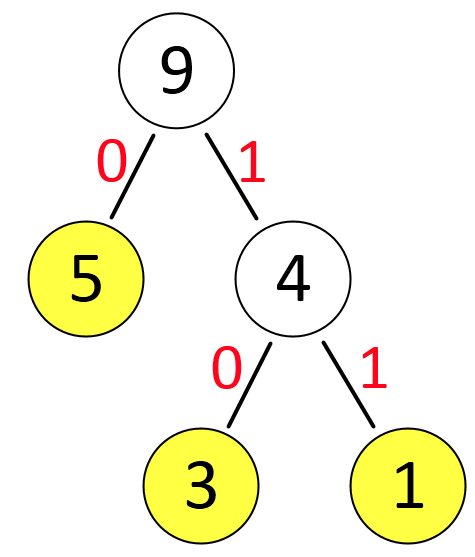
从 Huffman 树生成 Huffman 编码
编码规则:从叶子节点出发,沿路径向上到根节点,左子树路径记 “0”,右子树路径记 “1”,最后将记录的 “0/1” 反转,就是该字符的 Huffman 编码。
以 “ABABBCBBA” 的 Huffman 树为例:
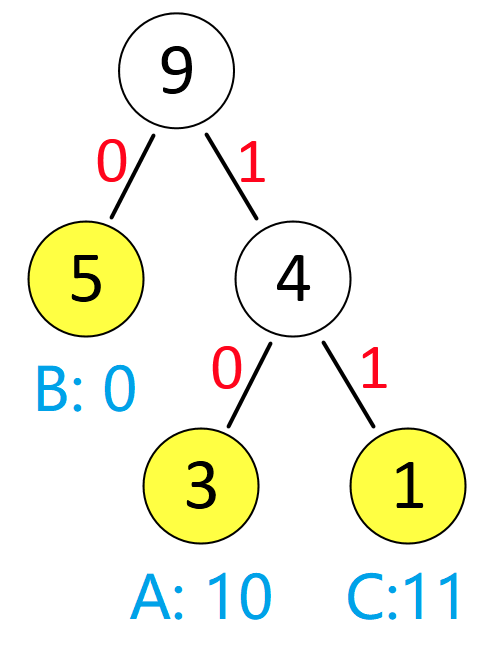
Huffman 编码的代码实现解析
以下代码基于 C 语言,实现 “统计字符→构建 Huffman 树→生成编码” 的完整流程,关键函数逐一解析。
初始化 Huffman 树(统计字符频次)
函数作用:输入字符串,统计每个字符的出现频次,初始化 Huffman 树的叶子节点。
// 参数:s=输入字符串,ht=Huffman树指针(输出),pm=叶子节点数(输出)
void initHuffmanTree(const char *s, HuffmanNode **ht, int *pm) {int freq[26] = {0}; // 假设只处理大写字母,A-Z对应索引0-25*pm = 0; // 初始化叶子节点数为0// 第一步:统计每个字符的频次for (int i = 0; s[i] != '\0'; i++) {freq[s[i] - 'A']++; // 如'A'-'A'=0,对应freq[0]}// 第二步:统计非0频次的字符数(即叶子节点数n0)for (int i = 0; i < 26; i++) {if (freq[i] != 0) {(*pm)++;}}// 第三步:初始化Huffman树数组(大小=2*pm-1)*ht = (HuffmanNode*)calloc(2 * (*pm) - 1, sizeof(HuffmanNode));for (int i = 0, k = 0; i < 26; i++) {if (freq[i] != 0) {(*ht)[k].ch = 'A' + i; // 赋值字符(*ht)[k].weight = freq[i]; // 赋值频次(权值)k++; // 只初始化前pm个叶子节点}}
}
找到两个最小权值的无父节点
函数作用:在 Huffman 树中,找到 “parent=0”(未合并)的两个权值最小的节点,返回其索引。
// 参数:ht=Huffman树,end=当前处理的最后一个节点索引,p1/p2=两个最小节点的索引(输出)
void findMin(HuffmanNode *ht, int end, int *p1, int *p2) {int min1 = INT_MAX, min2 = INT_MAX; // 初始设为最大整数*p1 = *p2 = 0;for (int i = 0; i <= end; i++) {if (ht[i].parent != 0) { // 已合并的节点跳过continue;}// 更新第一个最小值min1if (ht[i].weight < min1) {min2 = min1; // 原min1降为min2*p2 = *p1; // 原p1降为p2min1 = ht[i].weight;*p1 = i;} // 更新第二个最小值min2else if (ht[i].weight < min2) {min2 = ht[i].weight;*p2 = i;}}
}
构建 Huffman 树
函数作用:调用 findMin 函数,循环合并节点,填充 Huffman 树数组的非叶子节点。
// 参数:ht=Huffman树,m=叶子节点数(pm的值)
void createHuffmanTree(HuffmanNode *ht, int m) {int p1, p2; // 两个最小节点的索引// 从叶子节点后开始,填充合并节点(索引m到2m-2)for (int i = m; i < 2 * m - 1; i++) {findMin(ht, i - 1, &p1, &p2); // 找前i-1个节点中的两个最小值// 合并节点i:父节点是i,左子p1,右子p2ht[p1].parent = i;ht[p2].parent = i;ht[i].lchild = p1;ht[i].rchild = p2;ht[i].weight = ht[p1].weight + ht[p2].weight;}
}
生成 Huffman 编码
函数作用:从叶子节点向上遍历到根,记录路径(左 0 右 1),反转后输出编码。
// 参数:ht=Huffman树,i=叶子节点的索引
void getHuffmanCode(HuffmanNode *ht, int i) {char code[20] = {0}; // 存储临时路径(最多20位足够)int top = 0; // 记录路径长度(数组下标)int parent = ht[i].parent; // 当前节点的父节点int curr = i; // 当前节点索引// 从叶子到根,记录路径while (parent != 0) { // 根节点的parent=0,循环结束if (ht[parent].lchild == curr) { // 当前节点是父节点的左子树code[top++] = '0';} else { // 当前节点是父节点的右子树code[top++] = '1';}curr = parent; // 移动到父节点parent = ht[curr].parent; // 更新父节点}// 反转路径,输出编码(从后往前打印)printf("%c: ", ht[i].ch);for (int j = top - 1; j >= 0; j--) {printf("%c", code[j]);}printf("\n");
}
主函数(整合流程)
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#include <string.h>
// 先定义HuffmanNode结构体(见步骤2)int main(int argc, char const *argv[]) {if (argc != 2) { // 命令行输入字符串,如./huffman ABABBCBBAprintf("用法:%s <字符串>\n", argv[0]);return 1;}int leafCount; // 叶子节点数(字符种类数)HuffmanNode *huffTree; // Huffman树// 初始化Huffman树(统计频次)initHuffmanTree(argv[1], &huffTree, &leafCount);// 构建Huffman树createHuffmanTree(huffTree, leafCount);// 生成并打印Huffman编码表printf("Huffman编码表:\n");for (int i = 0; i < leafCount; i++) {getHuffmanCode(huffTree, i);}free(huffTree); // 释放内存return 0;
}
运行结果(输入 “ABABBCBBA”)
Huffman编码表:
A: 01
B: 1
C: 00
注:编码值可能因 “左 / 右子节点约定” 不同略有差异,如 B 的编码可能是 0,但长度一定是 1 位,符合高频短码原则。
