1.略
2.题目
贪心,流水线调度作业模型的 Johnson 不等式的运用,证明不会
1. 将所有 N 架飞船分成两个集合。集合\(S_1\)包含所有满足 \(U(i)≤V(i)\) 的飞船 \(i\)。集合 \(S_2\)
包含所有满足 \(U(i)>V(i)\) 的飞船 \(i\)。
2. 对集合 \(S1\) 中的飞船,按照它们的 \(U(i)\) 值进行升序排序。对集合 \(S_2\) 中的飞船,按照它们的 \(V(i)\) 值进行降序排序。
3.
题面:在平面上给\(n\)个坐标互不相同的点,保证没有三点共线,任选三个点组成一个三角形,一个三角形的权值定义为内部被覆盖的点的数量(不包含顶点),输出权值为0....n-3的三角形数量 (n<=300)
首先将点按\(x\)第一关键字,\(y\)第二关键字,升序排序
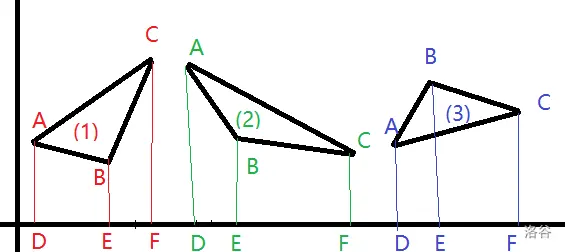
记\(sum[i][j]\)为在\(i\)与\(j\)的连线下方且满足\(x[i]<x<=x[j]\) 的点
分类讨论B点在 AC下还是上
若B在下方:三角形ABC的权值:\(sum[A][C]-sum[A][B]-sum[B][C]-1\)(-1是因为多算了顶点B)
若B在上方:三角形ABC的权值:\(sum[A][B]+sum[B][C]-sum[A][C]\)
