第一章 计算机系统漫游
考察Amdahl 定律
【练习题 1.1】
假设你是个卡车司机,要将土豆从爱达荷州的 Boise 运送到明尼苏达州的 Minneapolis, 全程 2500 公里。在限速范围内,你估计平均速度为 100 公里/小时,整个行程需要 25 个小时。
A. 你听到新闻说蒙大拿州刚刚取消了限速,这使得行程中有 1500 公里卡车的速度可以为 150 公里/小时。那么这对整个行程的加速比是多少?
B. 你可以为自己的卡车买个新的涡轮增压器。不过速度越快,价格越高。如果想要让整个行程的加速比为 1.67X ,那么你必须以多快的速度通过蒙大拿州?
【解A】
原本总耗时 = 25h
可改进部分为 1500 公里,原本用时 = 1500 / 100 = 15h,改进用时 = 1500 / 150 = 10h
改进部分的初始耗时比例 α = 15 / 25 = 0.6
加速比例因子 k = 15 / 10 = 1.5
加速比
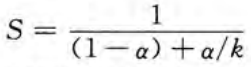
S = 1 / [0.4 + 0.6/1.5] = 1.25×
更直观的理解:
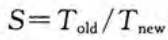
S = 25 / (10 + 10) = 1.25×
【解B】
原本总用时 / 改进总用时 = 1.67
改进总用时 = 原本总用时 / 1.67 = 25 / 1.67 ≈ 15 = 可改进部分用时 + 固定用时
可改进部分用时 = 15 - 固定用时 = 15 - 10 = 5h
速度 = 1500 / 5 = 300km/h
【练习题 1.2】
公司的市场部向你的客户承诺,下一个版本的软件性能将改进 2X 。这项任务被分配给你。你 已经确认只有 80% 的系统能够被改进,那么,这部分需要被改进多少(即 k 取何值)才能达到整体性能目标?
【解】
S = 原本总用时 / 改进总用时 = 2
设原本总用时2t,改进后总用时为t
可改进部分的原本用时 = 0.8 x 2t = 1.6t
不可改进部分用时 = 0.4t
2t / (可改进部分改进后用时 + 0.4t) = 2
可改进部分改进后用时 = 0.6t
k = 1.6t / 0.6t = 2.67
也可以直接套公式计算

