链接
A - Monotonic Matrix
以表格的形式画出 \(A\),发现最终表格一定形如一下形式。
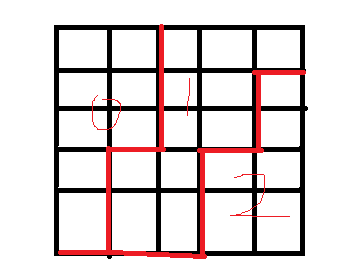
非常像 LGV 引理要求的形式,将 1 和 2 的交界线往下往右都移动一个点位,然后套 LGV 就可以了,答案是:
B - Symmetric Matrix
\(\sum\limits_{j}A_{ij} = 2\) 联想到图上的度数,每个点度数都为 2,表明图由多个环(包括二元环)组成,所以可以考虑每次加进去一个长为 \(k\) 的环进行计算,设 \(dp(n)\) 表示 \(n\) 时候的答案,(注意这里不能直接用环排列,要考虑对称的两个环相同的情况)那么有:
利用高中的化简功底,可以得到递推式:
C - Fluorescent 2
首先将三次方转化一下,设进行操作后,第 \(i\) 个位置的开关情况为 \(x_i\)(\(x_i = 0\) 表示关,\(x_i = 1\) 表示开),那么三次方就变成了:
再转化一下:
对三项分别计算即可。
先计算第一项,枚举每一项 \(i\),发现这时只和字符串第 \(i\) 列有关,如果该列全为 \(0\),则方案数为 \(2 ^ n\)。
接下来考虑存在至少一个 \(1\) 的情况,可以先选一个 \(1\),设其在第 \(t\) 行,那么另外 \(n - 1\) 个位置任意选或不选,选择完毕后如果开关开了,那么就可以不选第 \(t\) 行,反之就选,所以方案数为 \(2 ^ {n - 1}\)。
接下来计算第二项,这里可以枚举 \(i\) 和 \(j\),接下来为了方便,设第 \(i\) 列形成的二进制数为 \({bit}_i\),并且由于后面的方案数计算和计算第一项时类似,就不展开了,只给结论。
- \({bit}_i = {bit}_j = 0\),方案数为 \(2 ^ n\).
- \({bit}_i \neq 0, {bit}_j = 0\),方案数为 \(2 ^ {n - 1}\).
- \({bit}_i = {bit}_j \neq 0\),方案数为 \(2 ^ {n - 1}\).
- \({bit}_i \neq 0, {bit}_j \neq 0, {bit}_i \neq {bit}_j\),方案数为 \(2 ^ {n - 2}\).
然后是第三项,继续分类讨论,实现(计算每种情况的个数)见代码:
- \({bit}_i = {bit}_j = {bit}_k = 0\),\(2 ^ n\).
- \({bit}_i \neq 0, {bit}_j = {bit}_k = 0\),\(2 ^ {n - 1}\).
- \({bit}_i = {bit}_j \neq 0, {bit}_k = 0\),\(2 ^ {n - 1}\).
- \({bit}_i, {bit}_j\neq 0, {bit}_k = 0, {bit}_i \neq {bit}_j\),\(2 ^ {n - 2}\).
- \({bit}_i = {bit}_j = {bit}_k \neq 0\),\(2 ^ {n - 1}\).
- \({bit}_i, {bit}_j, {bit}_k\) 互不相等,都不为 \(0\),\({bit}_i \oplus {bit}_j = {bit}_k\),\(2 ^ {n - 2}\).
- \({bit}_i = {bit}_j \neq 0, {bit}_k \neq 0\),\(2 ^ {n - 2}\).
- \({bit}_i, {bit}_j, {bit}_k\) 互不相等,都不为 \(0\),\({bit}_i \oplus {bit}_j \neq {bit}_k\),\(2 ^ {n - 3}\).
(CHISHIGUANJUN)
int n, m; char s[N][M]; ll bit[M]; bool F[M];
map<ll, int> mp; mint pw[N], C[M][M];
int main() {ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int lim = 51;pw[0] = 1;forn (i, 1, lim) pw[i] = pw[i - 1] * mint(2);lim = 1000;C[0][0] = 1;forn (i, 1, lim) {C[i][0] = 1;forn (j, 1, lim) C[i][j] = C[i - 1][j] + C[i - 1][j - 1];}while (cin >> n >> m) {mp.clear();rep (i, 0, n) cin >> s[i];rep (j, 0, m) {bit[j] = 0;rep (i, 0, n) bit[j] = bit[j] << 1 | ((int)s[i][j] - int('0'));if (mp.count(bit[j])) F[j] = 0;else F[j] = 1;mp[bit[j]] ++ ;}mint ans = 0;// case 1 单个数字rep (i, 0, m) if (bit[i]) ans += pw[n - 1];else ans += pw[n];// case 2 两个数字rep (i, 0, m) rep (j, i + 1, m) if (!bit[i] && !bit[j]) ans += mint(6) * pw[n];else if (!bit[i] || !bit[j] || (bit[i] == bit[j])) ans += mint(6) * pw[n - 1];else ans += mint(n >= 2) * mint(6) * pw[n - 2];// case 3 三个数字mint cnt = C[m][3]; int n0 = 0;// case 3.1 bit[i] = bit[j] = bit[k] = 0if (mp.count(0ll)) {n0 = mp[0];cnt -= C[n0][3];ans += mint(6) * C[n0][3] * pw[n];}// case 3.2 bit[i] != 0, bit[j] = bit[k] = 0rep (i, 0, m) if (bit[i] && F[i]) //#ans += mint(6) * C[n0][2] * mint(mp[bit[i]]) * pw[n - 1],cnt -= C[n0][2] * mint(mp[bit[i]]);// case 3.3 bit[i] != 0, bit[j] != 0, bit[k] = 0 \and bit[i] = bit[j]rep (i, 0, m) if (bit[i] && F[i]) //#ans += mint(6) * C[mp[bit[i]]][2] * mint(n0) * pw[n - 1],cnt -= C[mp[bit[i]]][2] * mint(n0);// case 3.4 bit[i] != 0, bit[j] != 0, bit[k] = 0 \and bit[i] != bit[j]rep (i, 0, m) rep (j, i + 1, m) //#if (bit[i] && bit[j] && bit[i] != bit[j])ans += mint(n >= 2) * mint(6) * mint(n0) * pw[n - 2],cnt -= mint(n0);// case 3.5 bit[i] = bit[j] = bit[k] != 0;rep (i, 0, m) if (bit[i] && F[i]) //#ans += mint(6) * C[mp[bit[i]]][3] * pw[n - 1],cnt -= C[mp[bit[i]]][3];// case 3.6 bit[i], bit[j], bit[k] 互不相等,都不为零 bit[i] ^ bit[j] == bit[k]int cur = 0;rep (i, 0, m) rep (j, i + 1, m) // # if (bit[i] && bit[j] && mp.count(bit[i] ^ bit[j]) && (bit[i] ^ bit[j]))ans += mint(2) * mint(n >= 2) * mp[bit[i] ^ bit[j]] * pw[n - 2], cur += mp[bit[i] ^ bit[j]];cur /= 3, cnt -= mint(cur);// case 3.7 bit[i] = bit[j] != 0, bit[k] != 0rep (i, 0, m) if (bit[i] && F[i])ans += mint(6) * mint(n >= 2) * C[mp[bit[i]]][2] * mint(m - n0 - mp[bit[i]]) * pw[n - 2],cnt -= C[mp[bit[i]]][2] * mint(m - n0 - mp[bit[i]]);// case 3.8 bit[i], bit[j], bit[k] 互不相等,都不为零 bit[i] ^ bit[j] != bit[k]if (n >= 3) ans += mint(6) * cnt * pw[n - 3];cout << ans.r << '\n';}return 0;
}
E - Removal
首先不考虑去重,可以写出以下 DP,设 \(dp(n, m, t)\) 表示不去重情况下,考虑前 \(n\) 个数字,删除了 \(m\) 个,且最后一个为数字为 \(t\) 的方案数,有如下转移:
然后拿着这个东西取跑一遍样例,果真是错的,然后研究一下 DP 值,看看重复的都是什么情况。
这里以第一个样例为例,重复的点为去除前两个和后两个的两种情况,从 DP 转移的角度观察这个问题,当 \(n = 2\) 的时候,我们考虑 \(m = 1\) 和 \(m = 2\) 的情况:
m = 1: 子序列为 "1" 或 "2"
m = 2: 子序列为 ""
然后到了 \(n = 3\),我们会从 \(m = 1\) 转移出一个 "1",从 \(m = 2\) 转移出一个 "1",两个就重复了。
思考归纳一下,设两个序列为 pre 和 pre+s[i + 1] 那么前一种情况加上 \(s_{i + 1}\),后一种情况不加,就会出现重复。
所以去重的操作就是:
int n, m, k, s[N]; mint dp[N][11][11];
int main() {ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);while (cin >> n >> m >> k) {forn (i, 1, n) cin >> s[i];dp[1][0][s[1]] = 1;dp[1][1][0] = 1;rep (i, 1, n) forn (j, 0, m) {if (j) dp[i + 1][j][s[i + 1]] -= dp[i][j - 1][s[i + 1]];forn (t, 0, k) {dp[i + 1][j][s[i + 1]] += dp[i][j][t];if (j < m) dp[i + 1][j + 1][t] += dp[i][j][t];}}mint ans = 0;forn (t, 0, k) ans += dp[n][m][t];cout << ans.r << '\n';forn (i, 1, n) forn (j, 0, m) forn (t, 0, k) dp[i][j][t] = 0;}return 0;
}
F - Sum of Maximum
考虑枚举 \(k = \max\{x_1, x_2, \cdots, x_n\}\),求 \(k\) 会被算几次。
直接算比较困难,考虑算 \(\max\{x_1, x_2, \cdots, x_n\} \le k\) 的方案数,设为 \(S(k)\),可以发现,先对 \(a\) 进行排序,且令 \(a_0 = 0, a_{n + 1} = a_n + 1\),如果 \(m\) 为满足 \(a_m\le k < a_{m + 1}\) 的最大数字,那么有:
那么答案就是 \(\sum\limits_{k = 1} ^ {a_n} k (S(k) - S(k - 1))\),但是这个太慢了,考虑优化,直接推式子:
然后用拉格朗日插值或者伯努利数计算即可。
mint B[N], C[N][N], inv[N];
inline void table(int n = 1002) {C[0][0] = 1;forn (i, 1, n) {C[i][0] = 1;forn (j, 1, i) C[i][j] = C[i - 1][j - 1] + C[i - 1][j];}inv[1] = 1;forn (i, 2, n) inv[i] = mint(Mod - Mod / i) * inv[Mod % i];B[0] = 1;forn (i, 1, n - 1) {rep (k, 0, i) B[i] += C[i + 1][k] * B[k];B[i] *= mint(Mod-1) * inv[i + 1];}
}
mint Pw[N];
inline mint Spw(int n, int m) {mint ans = 0;Pw[0] = 1; n ++ ;forn (k, 1, m + 1) Pw[k] = Pw[k - 1] * mint(n);forn (k, 0, m) ans += C[m + 1][k] * B[k] * Pw[m + 1 - k];ans *= inv[m + 1];return ans;
}
int n, a[N];
inline mint S(int k) {if (k == 0) return mint(0);mint ans = 1; int m = 0;forn (i, 1, n) if (a[i] <= k && k < a[i + 1])m = i;forn (i, 1, m) ans *= mint(a[i]);ans *= q_pow(mint(k), n - m);return ans;
}
int main() {ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);table();while (cin >> n) {int Mx = 0;forn (i, 1, n) cin >> a[i], Mx = max(Mx, a[i]);sort (a + 1, a + n + 1);a[n + 1] = Mx + 1;mint ans = 0; mint Prd = 1;forn (i, 0, n) {if (a[i]) Prd *= a[i];if (a[i] == a[i + 1]) continue ;ans += mint(a[i]) * (S(a[i]) - S(a[i] - 1));if (a[i + 1] - a[i] == 1) continue ;ans += Prd * (Spw(a[i + 1] - 1, n - i + 1) - Spw(a[i], n - i + 1));ans -= Prd * (Spw(max(a[i + 1] - 2, 0), n - i + 1) - Spw(a[i] - 1, n - i + 1));ans -= Prd * (Spw(max(a[i + 1] - 2, 0), n - i) - Spw(a[i] - 1, n - i));}cout << ans.r << '\n';}return 0;
}
G - Steiner Tree
最小斯坦纳树计数,那么就要研究我们平常使用的计算最小斯坦纳树的方法。
两个转移:
- \(dp(i, S) \leftarrow dp(i, T) + dp(i, S\setminus T)\).
- \(dp(i, S) \leftarrow dp(j, S) + w(i, j)\).
考虑在 DP 的时候计数,那么第二个转移是没有问题的,但是第一个转移会数重。
具体来说,第二个转移后的有根斯坦纳树的根节点度数为 \(1\),假若之前计算的不重不漏,转移出来的也是不重不漏的。
但是由于原来只是一个最优化问题,第二个转移本只是解决根节点度数 \(>1\) 的情况,但通过度为 \(0\) 和度为 \(1\) 两个情况合并,也会是得出的度为 \(1\) 的结果,并且子集合并的顺序也会让方案出现重复。
为了让最终结果不重不漏,我们可以在子集 DP 中每次只用根节点度为 \(1\) 的树进行合并,再将这些树进行背包转移。
具体的,因为所有根节点度为 \(1\) 的树都来自于计算最短路,而其他情况都来自于子集 DP,所以我们将这两种情况分开。设 \(dp(i, S, 0)\) 表示所有情况的状态,\(dp(i, S, 1)\) 表示根节点度为 \(1\) 的情况的状态,在最短路时,用 \(dp(i, S, 0)\) 作为初始点,更新 \(dp(j, S, 0/1)\),在子集 DP 时,做一个背包,将 \(dp(i, S, 1)\) 作为物品的状态,\(S\) 为代价,\(dp(i, S, 0)\) 作为背包,进行转移,但是这里有一个子集顺序的问题,钦定编号最小的点由高到低位填即可,实现可以看代码。
struct node {int v, w;node() {}node(int _v, int _w) : v(_v), w(_w) {}bool operator < (const node &other) const {return w > other.w;}
};
int n, m, k, dp[N][1 << 12][2]; mint g[N][1 << 12][2];
bool vis[N];
vector<int> G[N];
priority_queue<node> Q;
inline void dij(int state) {rep (i, 0, n) vis[i] = 0;while (!Q.empty()) {int u = Q.top().v, w = Q.top().w;Q.pop();if (vis[u]) continue ;vis[u] = 1;for (int v : G[u]) rep (r, 0, 2) if (dp[v][state][r] > w + 1) {dp[v][state][r] = w + 1,g[v][state][r] = g[u][state][0];if (r == 0) Q.push(node(v, w + 1));}else if (dp[v][state][r] == w + 1)g[v][state][r] += g[u][state][0];}
}
int main() {ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);while (cin >> n >> m >> k) {while (m --> 0) {int u, v;cin >> u >> v;u -- , v -- ;G[u].push_back(v), G[v].push_back(u);}int inf = Mod / 10;rep (i, 0, n) rep (j, 0, 1 << k) rep (r, 0, 2)dp[i][j][r] = inf, g[i][j][r] = 0;rep (i, 0, k) rep (r, 0, 2)dp[i][1 << i][r] = 0, g[i][1 << i][r] = 1;int U = (1 << k) - 1;rep (S, 0, 1 << k) {rep (i, 0, n) {for (int T = (S - 1) & S; T; T = (T - 1) & S) if ((S & (-S)) == (T & (-T))) {if (dp[i][S][0] > dp[i][S ^ T][0] + dp[i][T][1])dp[i][S][0] = dp[i][S ^ T][0] + dp[i][T][1],g[i][S][0] = g[i][S ^ T][0] * g[i][T][1];else if (dp[i][S][0] == dp[i][S ^ T][0] + dp[i][T][1])g[i][S][0] += g[i][S ^ T][0] * g[i][T][1];}if (dp[i][S][0] < inf) Q.push(node(i, dp[i][S][0]));}dij(S);}cout << g[0][U][0].r << '\n';rep (i, 0, n) G[i].clear();}return 0;
}
H - Longest Path
首先考虑暴力 DP,然后发现暴力都不会。。。
问题在哪里呢,如果直接设 \(dp(u)\) 表示根节点为 \(u\) 的子树的答案,这个时候如果从儿子节点 \(v\) 转移过来,就会遇上麻烦,也就是你不知道儿子节点接下来的边是哪条。
所以我们转变思路,从枚举点改为枚举边,设 \(u\) 的父节点为 \({fa}_u\),那么 \(dp(u)\) 表示从 \({fa}_u\) 为起点且以边 \(({fa}_u, u)\) 为起始边的链的最大值,设 \(({fa}_u, u)\) 的边权为 \({val}_u\),这样就有转移:
这是一条向下的链,为了解决原题目,我们尝试求出以 \(u\) 为起点,\((u, {fa}_u)\) 为起始边的链的最大值 \(g(u)\),转移的时候发现需要遍历 \(u\) 的所有兄弟节点:
这样复杂度是 \(\mathcal {O}(n ^ 2)\) 的,但是第二个转移方程可以使用斜率优化方法进行优化:
所以就做完了,复杂度 \(\mathcal O(n\log n)\).
struct node {int v; ll w;node() {}node(int _v, ll _w) : v(_v), w(_w) {}
};
int n; vector<node> T[N];
ll dp[N][2], ans[N], val[N]; int fa[N], dfn[N], dn;
inline ll R(ll x) { return x * x; }
void Fdfs(int u) {dfn[++dn] = u;for (node e : T[u]) if (e.v != fa[u]) {fa[e.v] = u, val[e.v] = e.w, Fdfs(e.v);if (fa[u]) dp[u][1] = max(dp[u][1], dp[e.v][1] + R(val[e.v] - val[u]));}if (fa[u]) ans[fa[u]] = max(ans[fa[u]], dp[u][1]);
}
int top, stk[N], id[N];
inline bool check(int i, int j, int k) {ll X1 = val[i], X2 = val[j], X3 = val[k];// X1 < X2 < X3ll Y1 = dp[i][1] + R(val[i]), Y2 = dp[j][1] + R(val[j]), Y3 = dp[k][1] + R(val[k]);// l(i, k) < l(j, k)return (Y3 - Y1) * (X3 - X2) < (Y3 - Y2) * (X3 - X1);
}
inline bool cmp(ll k, int i, int j) {// k > l(i, j)ll X1 = val[i], X2 = val[j];// X1 < X2ll Y1 = dp[i][1] + R(val[i]), Y2 = dp[j][1] + R(val[j]);return k * (X2 - X1) > Y2 - Y1;
}
int main() {ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);while (cin >> n) {forn (i, 0, n) val[i] = ans[i] = dp[i][0] = dp[i][1] = 0;rep (i, 1, n) {int a, b; ll c;cin >> a >> b >> c;T[a].push_back(node(b, c));T[b].push_back(node(a, c));}dn = 0, Fdfs(1);forn (o, 1, n) {int u = dfn[o];int cnt = 0;for (node e : T[u]) if (e.v != fa[u]) {id[++cnt] = e.v;if (fa[u]) dp[e.v][0] = max(dp[e.v][0], dp[u][0] + R(val[u] - val[e.v])),ans[e.v] = max(ans[e.v], dp[e.v][0]);}sort (id + 1, id + cnt + 1, [&] (int a, int b) {return val[a] < val[b];});top = 0;forn (i, 1, cnt) {int s = id[i];while (top > 1 && cmp(2 * val[s], stk[top - 1], stk[top]))top -- ;if (top) dp[s][0] = max(dp[s][0], dp[stk[top]][1] + R(val[stk[top]] - val[s]));ans[s] = max(ans[s], dp[s][0]);while (top > 1 && check(stk[top - 1], stk[top], s))top -- ;stk[++top] = s;}top = 0;form (i, cnt, 1) {int s = id[i];while (top > 1 && cmp(2 * val[s], stk[top - 1], stk[top]))top -- ;if (top) dp[s][0] = max(dp[s][0], dp[stk[top]][1] + R(val[stk[top]] - val[s]));ans[s] = max(ans[s], dp[s][0]);while (top > 1 && !check(stk[top - 1], stk[top], s))top -- ;stk[++top] = s;}}forn (i, 1, n) cout << ans[i] << '\n';forn (i, 1, n) T[i].clear();}return 0;
}
I - Substring
SA 求子串个数
J - Different Integers
终于有简单题了
首先,如果只求区间 \([l, r]\) 中的答案,是一个原题。那么怎么转化成原题呢?只需要把 \(a_{i + n} = a_i\),然后求 \([r, l + n]\) 内的答案即可。
struct node {int l, id;node() {}node(int _l ,int _id) : l(_l), id(_id) {}
};
struct BIT {int val[N << 1], R;inline void init(int lim) { forn (i, 1, R) val[i] = 0; R = lim; }inline void upd(int p, int k) { while (p <= R) val[p] += k, p += p & -p; }inline int qry(int p) { int res = 0; while (p) res += val[p], p -= p & -p; return res; }inline int qry(int l, int r) { return qry(r) - qry(l - 1); }
} T;
int n, q, a[N << 1], ans[N], pre[N];
vector<node> Q[N << 1];
int main() {ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);while (cin >> n >> q) {forn (i, 1, n) cin >> a[i], a[i + n] = a[i], pre[i] = 0;forn (i, 1, q) {int l, r;cin >> l >> r;Q[l + n].push_back(node(r, i));}T.init(n << 1);forn (r, 1, n << 1) {if (pre[a[r]]) T.upd(pre[a[r]], -1);T.upd(r, 1), pre[a[r]] = r;for (node m : Q[r]) ans[m.id] = T.qry(m.l, r);}forn (i, 1, q) cout << ans[i] << '\n';forn (i, n + 1, n << 1) Q[i].clear();}return 0;
}
