定义
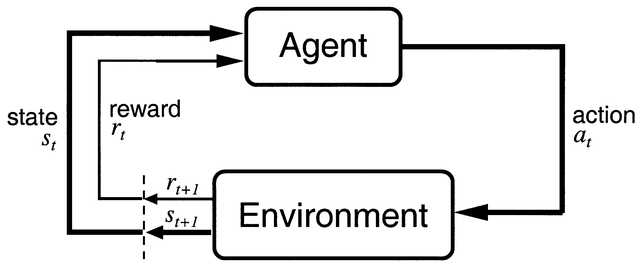
强化学习(Reinforcement Learning, RL)方法适用于智能体(agent)以离散时间步与环境交互的问题(@fig-agentenv)。
在时间 \(t\),智能体处于状态 \(s_t\),并决定执行一个动作 \(a_t\)。在下一时刻,它进入新的状态 \(s_{t+1}\),并获得奖励 \(r_{t+1}\)。
在一般情况下,状态转移和奖励都是随机的(即执行相同动作后到达不同状态的概率不同)。
智能体的目标是在长期内最大化获得的累计奖励。
这些问题被形式化为马尔可夫决策过程(MDP),定义为六元组:
对于一个有限MDP,有:
-
状态空间 \(\mathcal{S} = \{ s_i\}_{i=1}^N\),每个状态满足马尔可夫性质。
-
动作空间 \(\mathcal{A} = \{ a_i\}_{i=1}^M\)。
-
初始状态分布 \(p_0(s_0)\),表示智能体最有可能从哪些状态开始。
-
状态转移概率函数:
\[\begin{aligned}\mathcal{P}: \mathcal{S} \times \mathcal{A} \rightarrow & P(\mathcal{S}) \\p(s' | s, a) & = P (s_{t+1} = s' | s_t = s, a_t = a) \end{aligned} \] -
期望奖励函数:
\[\begin{aligned}\mathcal{R}: \mathcal{S} \times \mathcal{A} \times \mathcal{S} \rightarrow & \Re \\r(s, a, s') &= \mathbb{E} (r_{t+1} | s_t = s, a_t = a, s_{t+1} = s') \end{aligned} \] -
折扣因子 \(\gamma \in [0, 1]\)。
在深度强化学习(Deep RL)中,状态空间与动作空间可以是无限的,但我们先讨论有限MDP。
智能体的行为序列称为轨迹(trajectory)或回合(episode):
每个转移 \((s_t, a_t, s_{t+1})\) 以概率 \(p(s'|s,a)\) 发生,并产生奖励 \(r(s,a,s')\)。
在回合型任务中,时间跨度 \(T\) 有限;在持续型任务中,\(T\) 无限。
马尔可夫性质(Markov Property)
智能体的状态应包含做出决策所需的全部信息。
例如,一个机器人导航任务中,状态可能包括所有传感器读数、位置、与其他物体的相对位置等。
在棋类游戏中,棋盘的布局通常足以表示状态。
马尔可夫性质:未来与过去无关,只依赖当前状态。
形式化定义:
也就是说,只要当前状态定义完整,就不需要整个历史记录。
若问题不满足马尔可夫性质(例如观测部分缺失),RL算法可能不收敛。
这类问题称为部分可观测马尔可夫决策过程(POMDP)。
观测 \(o_t\) 来自观测空间 \(\mathcal{O}\),且满足 \(p(o_t | s_t)\)。
由于观测不是马尔可夫的,解决POMDP通常需要完整的观测历史 \(h_t = (o_0, a_0, ..., o_t, a_t)\),
这时循环神经网络(RNN)可用于帮助记忆历史。
奖励与回报(Rewards and Returns)
与bandit问题类似,我们关注期望奖励:
奖励可分为:
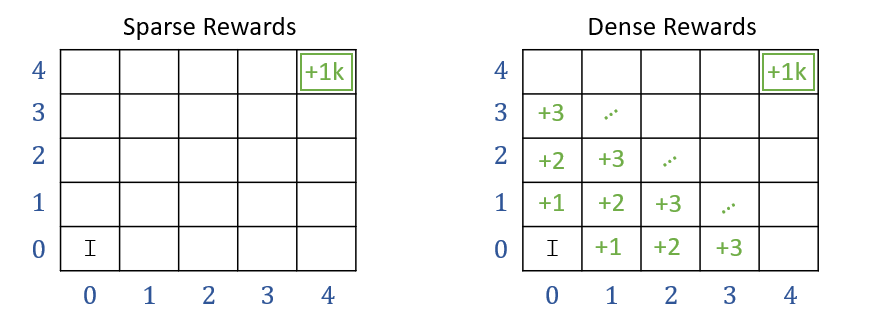
- 稀疏奖励(Sparse rewards):仅在关键事件(如胜利、失败、到达目标)时非零;
- 密集奖励(Dense rewards):每个时间步都提供奖励(如速度、距离、能耗等)。
稀疏奖励更难学习。
MDP经历状态序列:
并获得奖励序列:
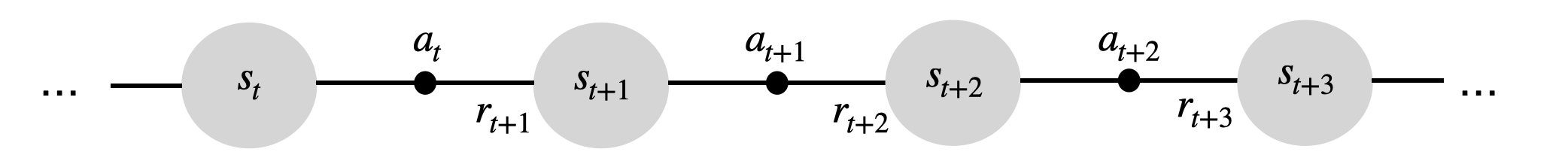
在MDP中,我们希望最大化回报(return):
其中 \(\gamma\) 为折扣因子(discount factor),表示未来奖励的现值。
\(\gamma\) 越小,智能体越短视;\(\gamma\) 越大,越远见。
- 对于回合型任务:\[R_t = \sum_{k=0}^{T} r_{t+k+1} \]
- 对于持续型任务:\[R_t = \sum_{k=0}^{\infty} \gamma^k \, r_{t+k+1} \]
为什么要看长期奖励?
某状态 \(s_1\) 下两个动作:
- \(a_1\):暂时无奖励,但未来可获 \(10\);
- \(a_2\):立即获得 \(1\)。
若 \(\gamma\) 大,\(a_1\) 更优;若 \(\gamma\) 小,\(a_2\) 更优。
因此,\(\gamma\) 决定了智能体的行为倾向。
策略(Policy)
智能体在状态 \(s\) 下选择动作 \(a\) 的概率称为策略 \(\pi\):
策略可以是确定性或随机性的,且满足:
目标是找到最优策略 \(\pi^*\),最大化长期期望回报:
价值函数(Value Functions)
强化学习的核心思想之一是:
评估每个状态或动作的好坏程度。
状态价值函数
动作价值函数(Q函数)
\(Q\) 值反映在状态 \(s\) 下执行动作 \(a\) 的期望回报。
贝尔曼方程(Bellman Equations)
\(V\) 与 \(Q\) 的关系
即:若策略确定,则 \(V\) 等于该动作的 \(Q\) 值;若随机,则是加权平均。
并且有递推关系:
取期望得:
贝尔曼方程形式
这些递归方程是强化学习的理论基础。
最优贝尔曼方程(Optimal Bellman Equations)
存在最优策略 \(\pi^*\),定义最优状态值与动作值:
此时:
动态规划(Dynamic Programming, DP)
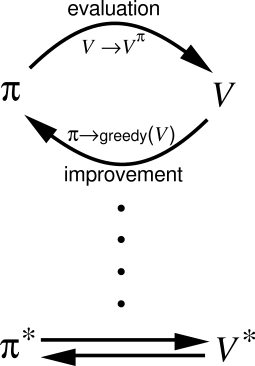
强化学习通常分为两步循环:
- 策略评估(Policy Evaluation):计算给定策略的 \(V^\pi\) 或 \(Q^\pi\);
- 策略改进(Policy Improvement):基于价值函数更新策略。
这种循环称为广义策略迭代(GPI)。
动态规划(DP)是其一种精确实现方式。
矩阵形式解法
设:
则贝尔曼方程写为:
解为:
但矩阵求逆复杂度高(\(\mathcal{O}(n^{2.37})\)),因此用迭代法近似。
策略迭代(Policy Iteration)
反复执行:
- 策略评估(使用贝尔曼方程更新 \(V\));
- 策略改进(基于 \(V\) 选择贪婪动作):
收敛后得到最优策略。
价值迭代(Value Iteration)
为加速收敛,将策略评估与改进交替进行:
即直接将贝尔曼最优方程转化为更新规则。
当 \(V\) 收敛时,即得最优值函数 \(V^*\)。
总结
策略迭代与价值迭代均基于贝尔曼方程与广义策略迭代(GPI)。
求解最优策略需:
- 了解环境动态 \(p(s'|s,a)\) 与 \(r(s,a,s')\);
- 足够的计算资源;
- 满足马尔可夫性质。
时间复杂度约为 \(\mathcal{O}(N^2 M)\)。
由于状态空间通常极大(如围棋约有 \(10^{170}\) 种状态),经典动态规划仅适用于小规模问题。
