盲猜你们都是从 CSP-S 2025 初赛 来的……
题目描述
给你 \(n\) 颗蛋和一个 \(m\) 层高的楼,定义蛋的硬度 \(k\) 为:在 \(<k\) 的楼层扔蛋不会碎,在 \(\ge k\) 的楼层扔蛋会碎。求在最坏情况下,最少需要扔多少次才能测出蛋的硬度。
数据范围:\(n \le 100,m \le 1000\)。
题目解析
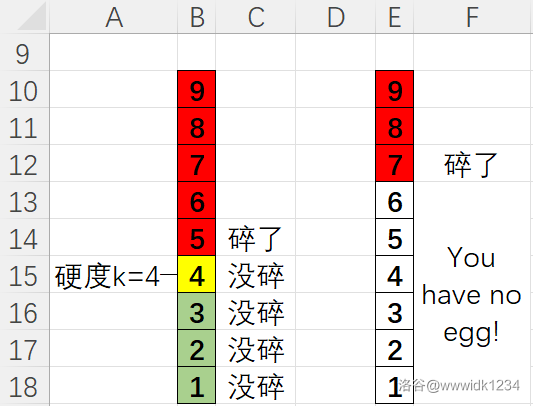
首先考虑只有 \(n=1\) 颗蛋的情况,这时只能从低到高一层一层试。因为只有一颗蛋,如果不一层一层试,蛋就可能会在一个 \(>k+1\) 的层爆掉了,导致没法准确测出蛋的硬度:
将情况拓展到任意颗蛋的情况:如果直接想“第 \(i\) 颗蛋选某一层楼扔下去,就要纠结“选哪一层扔下去一个蛋”,很难想?怎么办?发现最终题目求的是“最少次数”,扔一次蛋就能确定蛋在某一层有没有碎,所以我们考虑设 \(dp_{i,j}\) 表示给你 \(i\) 颗蛋和 \(j\) 次测试机会,最多能确定多少层的蛋状态(碎或不碎),这时就不用考虑在哪一层扔蛋的问题了。
怎么转移?假设我们在第 \(x\) 层扔了一个蛋,那么就有两种情况:蛋碎了和蛋没碎。
- 碎了:说明蛋的硬度 \(k \le x\),需要进一步测试,此时我们还剩 \(i-1\) 个蛋和 \(j-1\) 次机会,能够测出 \(dp_{i-1,j-1}\) 层楼的状态。
- 没碎:说明蛋的硬度 \(k>x\),需要进一步测试,此时我们还剩 \(i\) 颗蛋和 \(j-1\) 次机会,能够测出 \(dp_{i,j-1}\) 层楼的状态。
- 不管第 \(x\) 层碎没碎,我们已经测出了当前层的蛋状态。
所以得到状态转移方程:
初始状态是 \(\forall 1 \le j \le m,dp_{1,j}=j\),即只有一颗蛋的情况(只能一层一层测)。
参考程序:
AC 记录:https://www.spoj.com/status/ns=35026269#
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=211;
const int M=1218;
int caseid,n,m,ans=-1;
inline bool assert_ans(int h)
{if(h<0){printf("You have no egg!\n");return false;}else if(h>m){cerr<<h<<endl;printf("Wrong Answer!\n");return false;}else{printf("%d %d\n",caseid,h);return true;}
}
inline void guess1()
{vector< vector<int> > dp(n+2,vector<int>(m+2,0));ans=1218;for(int i=1;i<=n;i++) //使用i个egg{for(int j=1;j<=m;j++) //扔j次egg{if(i==1) dp[i][j]=j; //只有1个egg只能一次一次试else dp[i][j]=dp[i-1][j-1]+1+dp[i][j-1];if(dp[i][j]>=m) //能够确定m层楼,更新答案ans=min(ans,j);}}
}
int main()
{// freopen("neuvillette.in","r",stdin);// freopen("neuvillette.out","w",stdout);int T;scanf("%d",&T);while(T--) {scanf("%d%d%d",&caseid,&n,&m);if(n<=0) assert_ans(-12180211);else if(n==1) assert_ans(m);else{guess1();assert_ans(ans);}}cout.flush();return 0;
}
/*
dp[i][j]表示使用i个egg和扔j次egg最多能确定的楼层数
决策时需要考虑这一次扔egg碎没碎
*/
你说得对,但是《CSP-S 2025 初赛》是由 CCF 自主研发的开放世界冒险游戏。游戏发生在一个被称作「满线段树」的幻想世界,在这里,被模式串选中的人将被授予「next 数组」,导引 KMP 之力。你将扮演一位名为「机器规划员」的神秘角色,在自由的排列组合中邂逅性格各异、能力独特的方程的解,和他们一起走特殊最短路,找回失散的存在缺陷的生产线——同时,逐步发掘「You have no egg!」的真相。

