前言
对于attention操作,其计算复杂度随着序列长度的增加呈平方倍的增长。因此,出现了诸多尝试将计算复杂度降低为\(O(n)\)的注意力机制。然而,这些方法忽略了计算时的IO复杂度的影响,频繁的内存交换也在长序列计算attention产生了巨大时间延迟。flash attention通过减少内存交换,实现对attention的加速,已经成为目前常见的加速手段。本文回顾了flash attention,给出了flash attention详细解释和相关库的示例,希望能够更加深入的了解flash attention。
背景
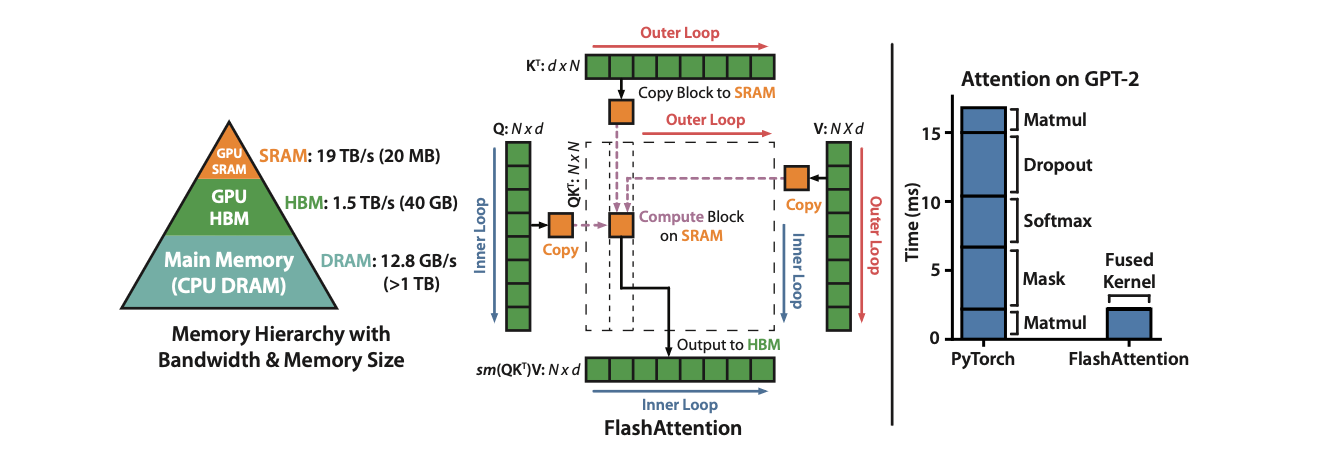
GPU采用大量线程(称为内核)进行操作,每个内核将HBM的数据加载到寄存器或SRAM进行计算,然后写回HBM中。
性能瓶颈
GPU计算中的性能瓶颈可以被归纳为两类:compute bound和memory bound。
compute bound: 计算时间主要消耗在算数运算上,而访存时间要短得多。经典的例子为大规模的矩阵乘法和卷积运算。
memory bound: 计算时间主要消耗在反复访问内存上,包括逐元素操作(elementwise),如activation、dropout等,和归约操作(reduction),如softmax、batchnorm、layernorm等。
kernel fusion: 编译器自动融合多个逐元素操作,只从HBM读取输入一次,而无需对每个操作重复读取并写入数据,缓解了memory bound。
flash attention通过减少访存HBM次数,进而加速attention计算,让整个注意力计算从memory bound转变为compute bound,从而充分利用了GPU强大的计算能力,实现了大幅加速。
Flash Attention
flash attention包含tiling和recomputation两个重要部分。前者将\(Q, K, V\)矩阵分片加载到SRAM上,减少了IO时间;后者在保存时,只保存统计量\(m, l\),将额外的内存消耗从\(O(N^{2})\)降低到了\(O(N)\)。
Tiling
假设\(x \in \mathbb{R}^{2B}\),则
考虑到softmax的数值稳定性,计算时,减去\(x\)的最大值,上式转化为
当矩阵过大,需要考虑如何分块计算softmax。假设\(x=[x^{1}, x^{2}]\),\(x_{1}, x_{2} \in \mathbb{R}^{B}\),对应的softmax可以独立计算
此时,有
因此,只需要维护\(m\)和\(l\)即可实现分块计算。
我们将上述结论应用到attention的计算中。假设\(Q, K, V \in \mathbb{R}^{N \times d}\)。将\(Q\)划分为\(T_{r}\)个子块\(Q_{i} \in \mathbb{R}^{B_{r}\times d}\),将\(K, V\)划分为\(T_{c}\)个子块\(K_{j}, V_{j} \in \mathbb{R}^{B_{c}\times d}\)。遍历\(T_{r}\)次,即可得到所有\(Q_{i}\)对应的输出\(O_{i}\),再遍历\(T_{c}\)次,即可得到完整的输出\(O\)。
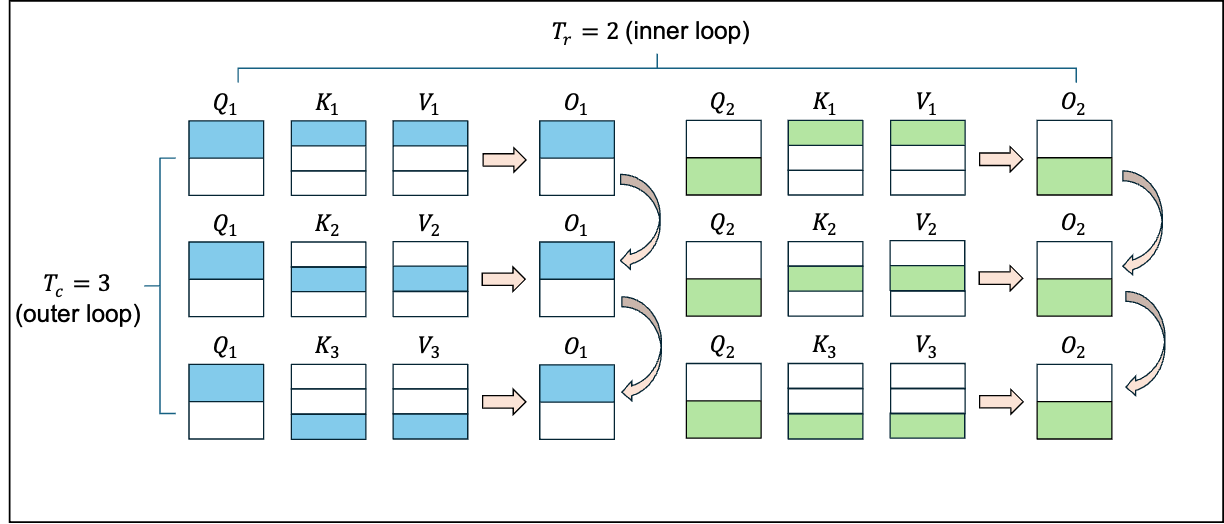
我们以\(O_{1}\)的计算为例,采用如下初始化统一迭代过程
第一轮计算:
由于softmax是逐行操作,因此计算\(m, l\)时采用逐行操作\(rowmax, rowsum\)。矩阵左乘对角阵代表按行进行缩放,因此,softmax归一化时需要左乘\(diag(l)\)或\(diag(l^{-1})\)。
第二轮计算
第三轮计算
因此,\(Q_{i}\)和\(K_{j}, V_{j}\)的attention计算可以统一为
Recomputation
在计算attention时,避免直接存储\(O(N^{2})\)的中间变量\(S\)和\(P\),可以直接存储\(O(N)\)的统计量\(m\)和\(l\),在反向传播时,重新计算\(S\)和\(P\)。因此,相较于标准的attention操作,flash attention的FLOPs略有增加,但由于其优化了IO读取效率,整体计算时间大幅减少。
Forward pass
Standard Attention

FLOPs计算:
\(S=QK^{T}\)的FLOPs为\(O(N^{2}d)\)
\(P=softmax(S)\)的FLOPs为\(O(N^{2})\)
\(O=PV\)的FLOPs为\(O(N^{2}d)\)
因此,总FLOPs为\(O(N^{2}d)\)
IO复杂度计算:
读入\(Q, K\)并写回\(S\)的IO复杂度为\(O(Nd+N^{2})\)
读入\(S\)并写回\(P\)的IO复杂度为\(O(N^{2})\)
读入\(P, V\)并写回\(O\)的IO复杂度为\(O(Nd+N^{2})\)
因此,总IO复杂度为\(O(Nd+N^{2})\)
Flash Attention

为了保证所有的分块变量能够加载到SRAM上,有
考虑到\(Q_{i}, O_{i} \in \mathbb{R}^{B_{r}\times d}\),\(K_{j}, V_{j} \in \mathbb{R}^{B_{c}\times d}\),当\(B_{r}=B_{c}=B\)时,有
因此在设置block size的时候,令
FLOPs计算:
\(S_{ij}=\tau Q_{i}K^{T}_{j}\)的FLOPs为\(O(B_{r}B_{c}d)\)
\(P_{ij}V_{j}\)的FLOPs的为\(O(B_{r}B_{c}d)\)
循环次数为\(T_{c}T_{r}\),因此总FLOPs为\(O(T_{c}T_{r}B_{r}B_{c}d)=O(N^{2}d)\)
IO复杂度计算:
读入\(T_{c}\)次\(K_{j}, V_{j}\) IO复杂度为\(O(T_{c}B_{c}d)=O(Nd)\)
读入\(T_{c}T_{r}\)次\(Q_{i}, O_{i}\),写入\(T_{c}T_{r}\)次\(O_{i}\),IO复杂度为\(O(T_{c}T_{r}B_{r}d)=O(NdT_{c})=O(Nd\frac{N}{B_{c}})=O(N^{2}d^{2}M^{-1})\)
因此,总IO复杂度为\(O(Nd+N^{2}d^{2}M^{-1})\)
我们以A100为例,SRAM的容量为192KB,对应的\(M=\frac{192*1024 Byte}{2 Byte}=98304\),主流的通道数为\(d=64, 128\),此时,\(\frac{d^{2}}{M}=\frac{1}{24}, \frac{1}{6}\)。因此,相较于标准attention运算,flash attention的IO复杂度减小24倍或6倍。
Backward pass
前置知识
-
softmax导数
假设\(y=softmax(x), x \in \mathbb{R}^{n}\),对应的雅可比矩阵为\[\begin{align} J &= \begin{bmatrix} \frac{\partial y_{1}}{\partial x_{1}} & \frac{\partial y_{1}}{\partial x_{2}} & \dots & \frac{\partial y_{1}}{\partial x_{n}} \\ \frac{\partial y_{2}}{\partial x_{1}} & \frac{\partial y_{2}}{\partial x_{2}} & \dots & \frac{\partial y_{2}}{\partial x_{n}} \\ \dots & \dots & \dots & \dots \\ \frac{\partial y_{n}}{\partial x_{1}} & \frac{\partial y_{n}}{\partial x_{2}} & \dots & \frac{\partial y_{n}}{\partial x_{n}} \\ \end{bmatrix} \notag \\ &= \begin{bmatrix} y_{1}(1-y_{1}) & -y_{1}y_{2} & \dots & -y_{1}y_{n} \\ -y_{1}y_{2} & y_{2}(1-y_{2}) & \dots & -y_{2}y_{n} \\ \dots & \dots & \dots & \dots \\ -y_{1}y_{n} & -y_{2}y_{n} & \dots & y_{n}(1-y_{n}) \\ \end{bmatrix} \notag \\ &= diag(y)-yy^{T} \notag \end{align} \] -
矩阵导数
假设\(O=PV\),已知\(dO\),求\(dP, dV\),其中,\(O, V \in \mathbb{R}^{N\times d}\),\(P \in \mathbb{R}^{N\times N}\),\([dO]_{ij}=\frac{\partial{\phi}}{\partial{O_{ij}}}\),\(\phi\)为标量损失函数。\[[dV]_{ij}=\frac{\partial{\phi}}{\partial{V_{ij}}}=\sum_{k=1}^{N}\frac{\partial{\phi}}{\partial{O_{kj}}}\frac{\partial{O_{kj}}}{\partial{V_{ij}}}=\sum_{k=1}^{N}[dO]_{kj}P_{ki}=\sum_{k=1}^{N}[P^{T}]_{ik}[dO]_{kj} \]因此,\(dV=P^{T}dO\)
\[[dP]_{ij}=\frac{\partial{\phi}}{\partial{P_{ij}}}=\sum_{k=1}^{d}\frac{\partial{\phi}}{\partial{O_{ik}}}\frac{\partial{O_{ik}}}{\partial{P_{ij}}}=\sum_{k=1}^{d}[dO]_{ik}V_{jk}=\sum_{k=1}^{d}[dO]_{ik}[V^{T}]_{kj} \]因此,\(dP=dOV^{T}\)
假设\(P, S \in \mathbb{R}^{N\times N}\),\(P=softmax(x)\), 已知\(dP\),求\(dS\)
\[[dS]_{ij} = \frac{\partial{\phi}}{\partial{S_{ij}}}=\sum_{k=1}^{N}\frac{\partial{\phi}}{\partial{P_{ik}}}\frac{\partial{P_{ik}}}{\partial{S_{ij}}}=[dP]_{ij}P_{ij}-\sum_{k=1}^{N}[dP]_{ik}P_{ik}P_{ij}=P_{ij}([dP]_{ij}-\sum_{k=1}^{N}[dP]_{ik}P_{ik}) \]因此,\(dS=P\odot (dP - rowsum(dP\odot P))\)。应当指出的是,在计算\(dS\)时,\(P, dP\)均已知,上式已经可以用来计算\(dS\)。但为了和原始的flash attention论文公式保持一致,我们做如下的变换
\[\sum_{k=1}^{N}[dP]_{ik}P_{ik}=\sum_{k=1}^{N}\sum_{j=1}^{d}[dO]_{ij}[V^{T}]_{jk}P_{ik}=\sum_{j=1}^{d}[dO]_{ij}\sum_{k=1}^{N}P_{ik}V_{kj}=\sum_{j=1}^{d}[dO]_{ij}O_{ij} \]因此,上式可以转化为
\[dS=P\odot (dP - rowsum(dO\odot O)) \]
Standard Attention

FLOPs计算:
计算\(dV, dP, dQ, dK\)的FLOPs均为\(O(N^{2}d)\)
计算\(dS\)的FLOPs为\(O(N^{2})\)
因此,总FLOPs为\(O(N^{2}d)\)
IO复杂度计算:
第一步的IO复杂度为\(O(N^{2}+Nd)\)
第二步的IO复杂度为\(O(N^2+Nd)\)
第三步的IO复杂度为\(O(N^2)\)
第四步的IO复杂度为\(O(N^{2}+Nd)\)
第五步的IO复杂度为\(O(N^{2}+Nd)\)
因此,总IO复杂度为\(O(N^{2}+Nd)\)
Flash Attention
反向传播时,由于\(m, l\)都已知,因此不需要额外进行迭代。假设\(Q, K, V, dO \in \mathbb{R}^{N \times d}\)。将\(Q\)划分为\(T_{r}\)个子块\(Q_{i} \in \mathbb{R}^{B_{r}\times d}\),将\(K, V\)划分为\(T_{c}\)个子块\(K_{j}, V_{j} \in \mathbb{R}^{B_{c}\times d}\)。
初始化: \(dK_{j}=dV_{j}=0\)
inner loop:

FLOPs计算:
计算\(S_{ij}\)的FLOPs为\(O(B_{r}B_{c}d)\),计算\(P_{ij}\)的FLOPs为\(O(B_{r}B_{r})\),计算\(dV_{j}, dP_{ij}, dK_{j}, dQ_{i}\)的FLOPs均为\(O(B_{r}B_{c}d)\),计算\(dS_{ij}\)的FLOPs为\(O(B_{r}B_{c})\)。因此,inner loop中总FLOPs为\(O(B_{r}B_{c}d)\)。循环次数为\(T_{c}T_{r}\),总FLOPs为\(O(T_{c}T_{r}B_{r}B_{c}d)=O(N^{2}d)\)。
IO复杂度计算:
读取\(K_{j}, V_{j}\)并写入\(dK_{j}, dV_{j}\)共\(T_{c}\)次,IO复杂度为\(O(T_{c}B_{c}d)=O(Nd)\)
读取\(Q_{i}, O_{i}, dO_{i}, dQ_{i}\)并写入\(dQ_{i}\)共\(T_{c}T_{r}\)次,IO复杂度为\(O(T_{c}T_{r}B_{r}d)=O(NdT_{c})\)
因此,总IO复杂度为\(O(NdT_{c}+Nd)=O(Nd+N^{2}d^{2}M^{-1})\)。
Code
flash_attn_func是最常用的函数,其中一个批次中的所有序列都被填充到相同的最大长度。
flash_attn_func(q,k,v,dropout_p=0.0,softmax_scale=None,causal=False,return_attn_probs=False
)
- q, k, v:
尺寸为[batch_size, seq_len, num_heads, head_dim] - dropout_p:
注意力权重的dropout概率,默认为0 - softmax_scale:
注意力矩阵的缩放系数,默认为\(\frac{1}{\sqrt{d}}\) - causal:
是否采用因果注意力机制 - return_attn_probs:
是否输出注意力矩阵
示例:
import torch
from flash_attn import flash_attn_func# 定义输入参数
batch_size = 4
seq_len = 1024
num_heads = 12
head_dim = 64# 创建随机输入张量
q = torch.randn(batch_size, seq_len, num_heads, head_dim, device='cuda', dtype=torch.bfloat16)
k = torch.randn(batch_size, seq_len, num_heads, head_dim, device='cuda', dtype=torch.bfloat16)
v = torch.randn(batch_size, seq_len, num_heads, head_dim, device='cuda', dtype=torch.bfloat16)# 调用 flash_attn_func
output = flash_attn_func(q, k, v, causal=True)# 打印输出形状
print(output.shape)
# torch.Size([4, 1024, 12, 64])
当一个批次中的序列长度不同时,标准的做法是先填充。但这会在填充部分进行大量无效计算。flash_attn_varlen_func 通过接收一个“无填充”的拼接张量和一个描述序列边界的索引来解决这个问题,从而获得更高的性能。
flash_attn_varlen_func(q,k,v,cu_seqlens_q,cu_seqlens_k,max_seqlen_q,max_seqlen_k,dropout_p=0.0,softmax_scale=None,causal=False
)
- q, k, v:
尺寸[sum(seq_len), num_heads, head_dim] - cu_seqlens_q, cu_seqlens_k:
[bacth_size+1, ],每个序列的开始和结束位置,如[0, seq_len1, seq_len2, ..., sum(seq_len)] - max_seqlen_q, max_seqlen_k:
当前batch中最长的序列长度,max(seq_len),用于指导分块策略 - dropout_p:
注意力权重的dropout概率,默认为0 - softmax_scale:
注意力矩阵的缩放系数,默认为\(\frac{1}{\sqrt{d}}\) - causal:
是否采用因果注意力机制
示例:
import torch
from flash_attn import flash_attn_varlen_func# 定义输入参数
batch_size = 3
num_heads = 12
head_dim = 64
# 假设批次中三个序列的真实长度不同
seqlens = [1280, 5120, 2560]# 计算 total_tokens 和 cu_seqlens
total_tokens = sum(seqlens)
# cu_seqlens: [0, 1280, 1280+5120, 1280+5120+2560] -> [0, 1280, 6400, 8960]
cu_seqlens = torch.tensor([0] + list(torch.cumsum(torch.tensor(seqlens), dim=0)), dtype=torch.int32, device='cuda')
max_seqlen = max(seqlens)# 创建拼接后的输入张量
q = torch.randn(total_tokens, num_heads, head_dim, device='cuda', dtype=torch.bfloat16)
k = torch.randn(total_tokens, num_heads, head_dim, device='cuda', dtype=torch.bfloat16)
v = torch.randn(total_tokens, num_heads, head_dim, device='cuda', dtype=torch.bfloat16)# 调用 flash_attn_varlen_func
output = flash_attn_varlen_func(q, k, v,cu_seqlens_q=cu_seqlens,cu_seqlens_k=cu_seqlens,max_seqlen_q=max_seqlen,max_seqlen_k=max_seqlen,causal=True
)# 打印输出形状
print(output.shape)
# torch.Size([8960, 12, 64])
后记
本文回顾了flash attention的计算公式,计算了标准attention和flash attention的FLOPs和IO复杂度,并给出了相应代码库的使用。
总而言之,flash attention由两个核心点,tiling和recomputation,tiling通过分块操作,将IO复杂度由\(O(Nd+N^{2})\)降低为\(O(Nd+N^{2}d^{2}M^{-1})\);recomputation通过只存储\(O(N)\)的中间变量,避免了对\(O(N^{2})\)中间变量的存储,稍微增加了FLOPs,但显著节省了显存。
参考
https://arxiv.org/abs/2205.14135
