
一、什么是RNN
按照八股文来说:RNN实际上就是一个带有记忆的时间序列的预测模型

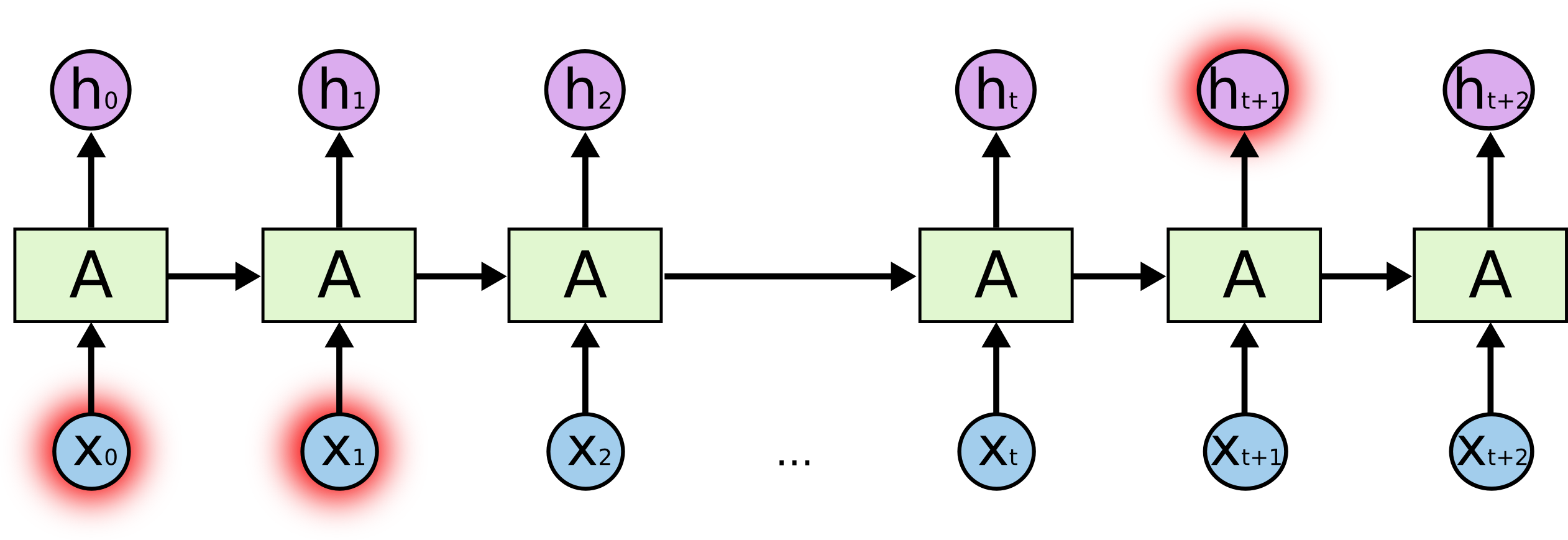
RNN的细胞结构说明
softmax激活函数只是我举的一个例子,实际上得到\(y_t\)也可以通过其他的激活函数得到。
其中\(a_{t-1}\)代表t-1时刻隐藏状态,\(a_t\)代表经过\(X_t\)(t时刻的输入)之后,得到的新的隐藏状态。核心公式为:
\(a_t = \tanh(W_{aa} \cdot a_{t-1} + W_{ax} \cdot X_t + b_1)\)
大白话解释:\(X_t\)是“今天的吊针”,\(a_{t-1}\)是“昨天的发烧度数39℃”,经过今天这一针后,\(a_t\)变成38℃。这里的“记忆”体现在:今天的38℃是在前一天状态的基础上,结合当前输入(吊针)更新得到的。
1.1 RNN的应用

由于RNN的记忆性,其最典型的应用场景是自然语言处理(如预测下一个字),除此之外还包括以下方向:
- 语言模型:广泛用于自然语言处理、机器翻译、语音识别等领域,建模语言的语法和语义规律。
- 时间序列预测:用于股票价格预测、气象预测、心电图信号预测等,捕捉时序数据的趋势变化。
- 生成模型:支持文本生成、音乐生成、艺术创作等,基于历史序列生成新的连贯内容。
- 强化学习:应用于游戏AI、机器人控制、决策制定等,让智能体根据历史交互调整策略。
1.2 RNN的缺陷
想必大家一定听说过LSTM——正是因为RNN的“局限性”,才催生了LSTM这种更精妙的时序预测模型。要理解LSTM,需先明确RNN的核心缺陷(多数资料仅提及结论,此处补充推导逻辑):
RNN的主要缺陷有两个:
- 长期依赖导致的梯度消失:RNN的预测依赖当前输入和历史状态,但当序列过长(如句子包含1000个词)时,第1000个记忆细胞几乎无法利用第1个细胞的信息,导致“长期记忆失效”。
- 梯度爆炸:序列较长时,梯度可能因连乘效应变得极大,导致模型参数更新失控。
1.2.1 梯度消失和梯度爆炸的详细公式推导
敲黑板(手写公式推导,大家最迷糊的地方):
根据下图示例(原文提及图示,此处省略),我手写并反复检查了推导过程,请务必认真理解——比其他文章“随口一提”的解释更透彻!
- 前提假设:设损失函数为\(L\)(\(Y\)为实际值,\(O\)为预测值),仅分析3层RNN(可类推至多层);反向传播需对\(W_o、W_x、W_s、b\)求偏导,此处重点分析\(W_x\)的偏导(其他参数逻辑一致);用“紫色x”表示乘法运算。


2. 核心结论:推导后得到梯度含指数项(高中知识可知,指数函数变化系数极大):
- 若指数项系数<1且序列较长(t较大):梯度会趋于0,模型优化几乎停止(梯度消失);
- 若指数项系数>1且序列较长(t较大):梯度会急剧增大,模型参数变化失控(梯度爆炸)。
二、什么是LSTM
八股文解释:LSTM(长短时记忆网络)是一种常用于处理序列数据的深度学习模型。与传统RNN相比,LSTM引入了三个门(输入门、遗忘门、输出门) 和一个细胞状态(cell state),这些机制能有效解决RNN的长期依赖问题。
注意:“小蝌蚪形状”的激活函数为sigmoid。
其中,\(C_t\)是细胞状态(核心记忆载体),\(X_t\)是t时刻输入信息,\(h_t\)是隐藏状态(基于\(C_t\)生成)。
用“两门考试”类比LSTM的三个门
用最朴素的语言解释三个门的作用,以“复习线性代数→复习高等数学”的场景类比:
- 遗忘门:通过\(X_t\)(高数复习内容)和\(h_{t-1}\)(线代复习记忆)的运算,结合sigmoid得到0-1向量——0代表“忘记线代中与高数无关的内容(如矩阵的秩)”,1代表“保留线代中与高数相关的内容(如数学运算规则)”。
- 输入门:将“遗忘门保留的线代记忆”与“当前高数的新记忆(如洛必达法则)”相加,更新为新的细胞状态\(C_t\)(即“线代+高数”的融合记忆)。
- 输出门:对新细胞状态\(C_t\)进行整合,生成隐藏状态\(h_t\)——类比“高数考试时的实际发挥”(未必能完全调用所有记忆,因此\(h_t\)对应“考试分数”)。
数据处理流程图示
为便于理解LSTM的完整逻辑,附上以下关键步骤的示意图(原文提及,此处保留说明):
- 遗忘门数据处理示意图
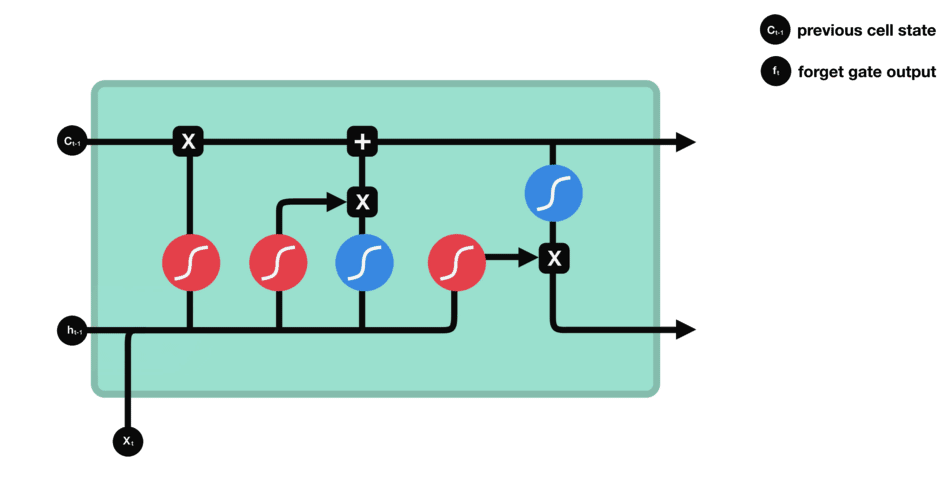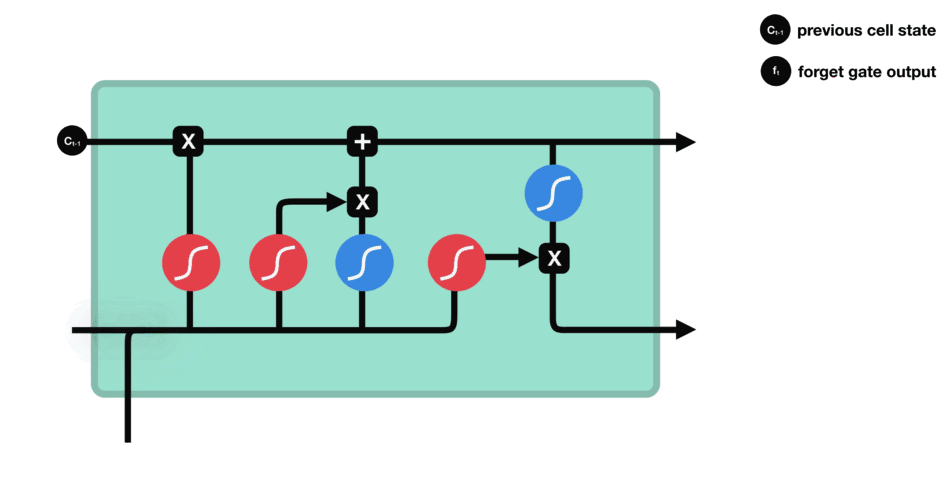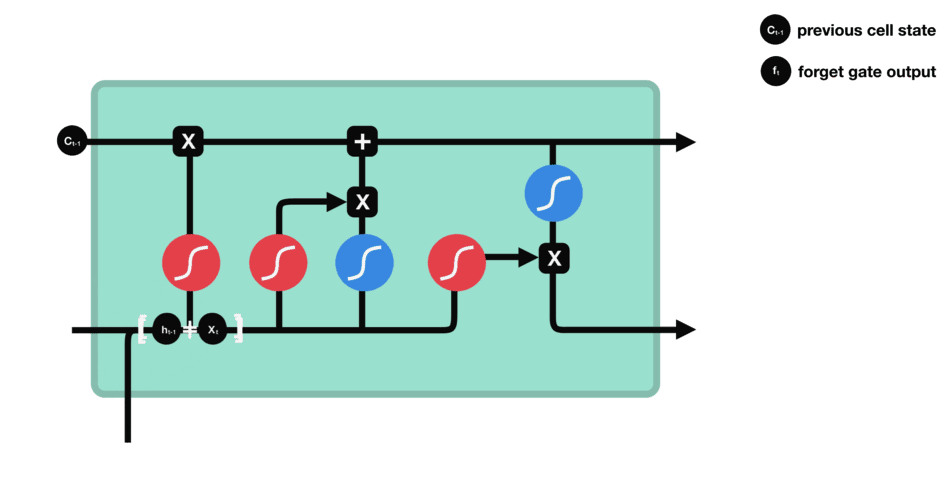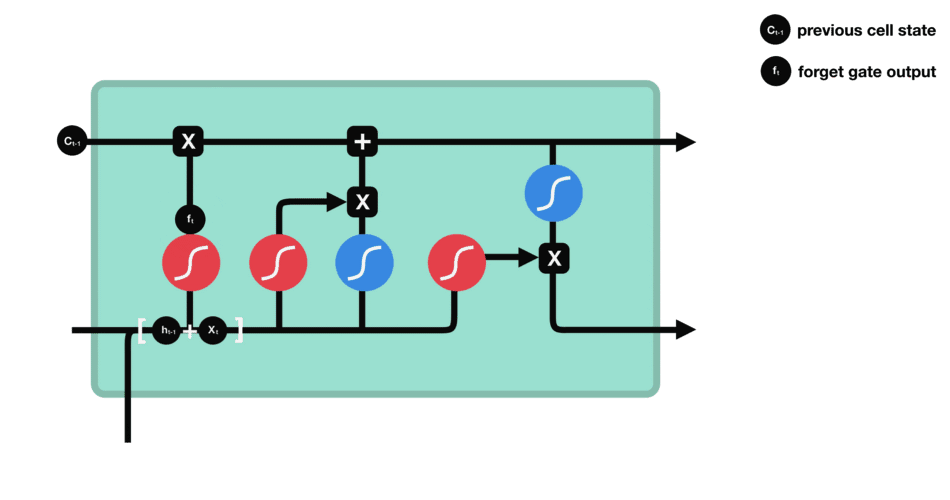
- 输入门数据处理示意图
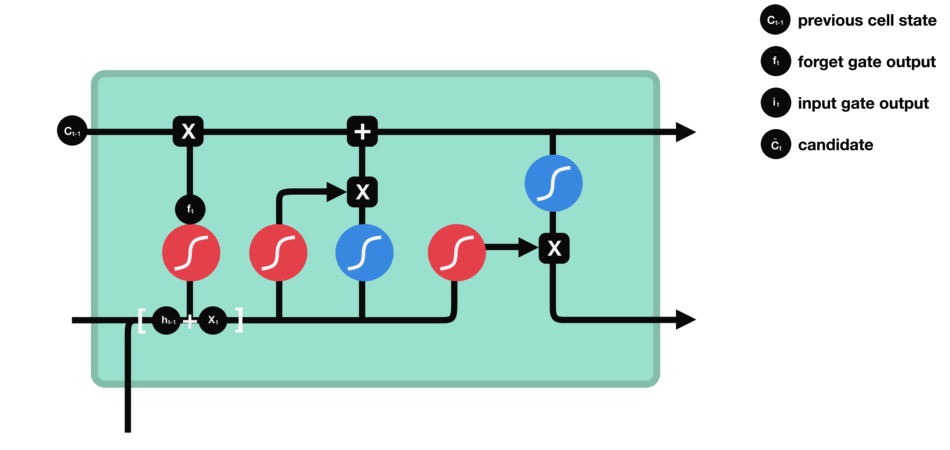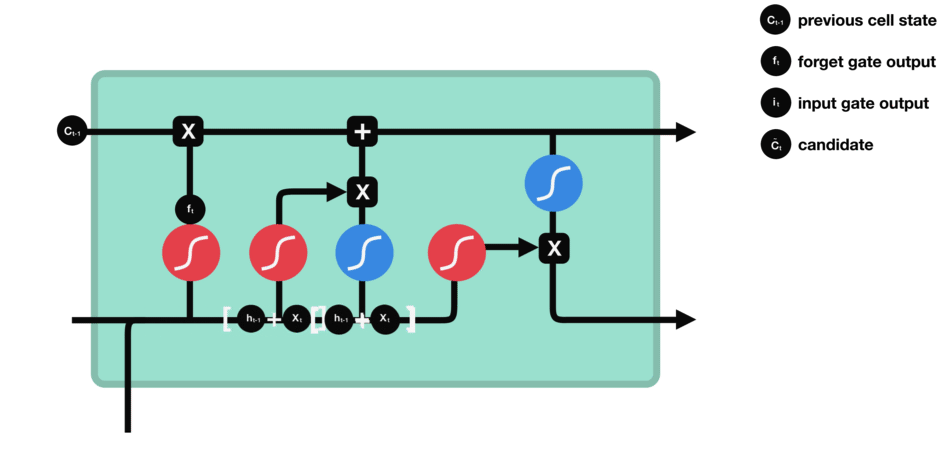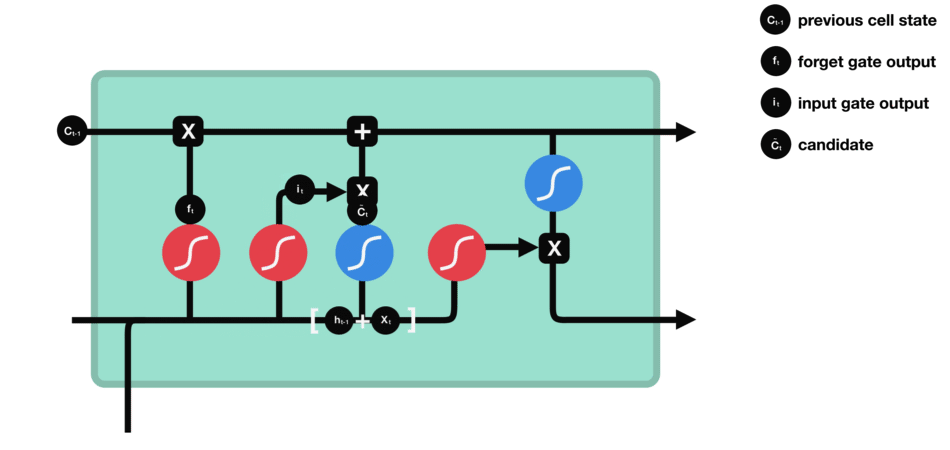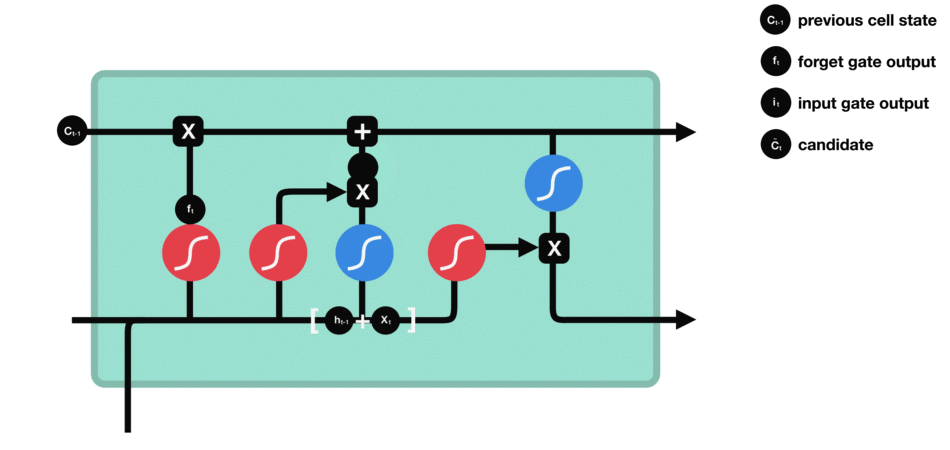
- 细胞状态更新示意图

- 输出门数据处理示意图
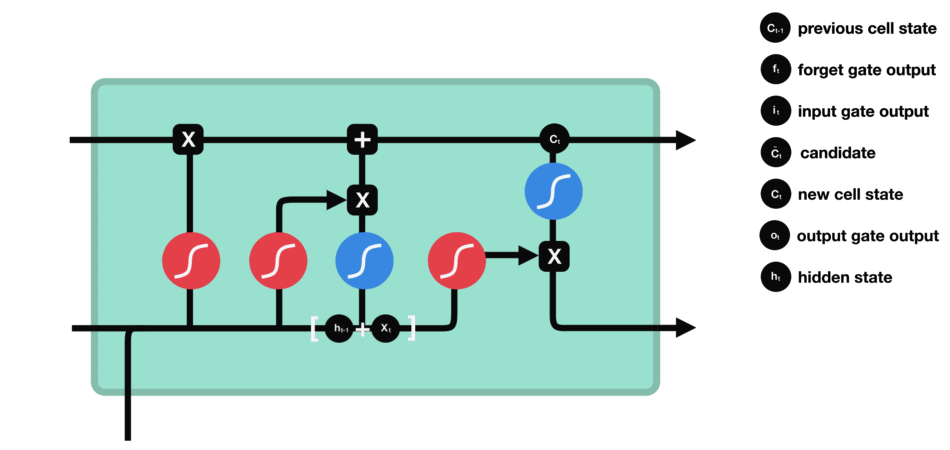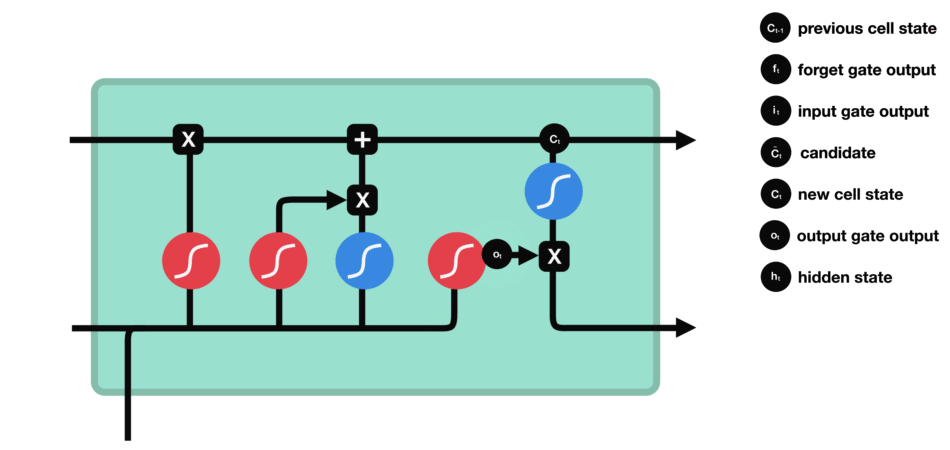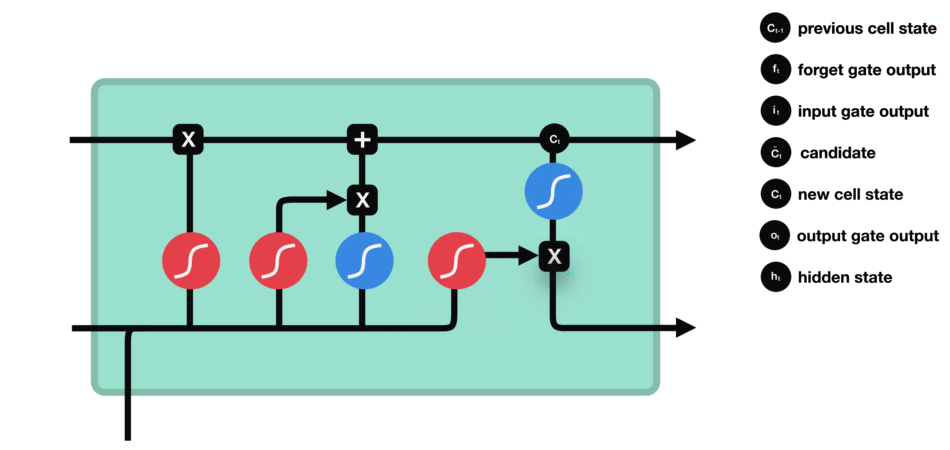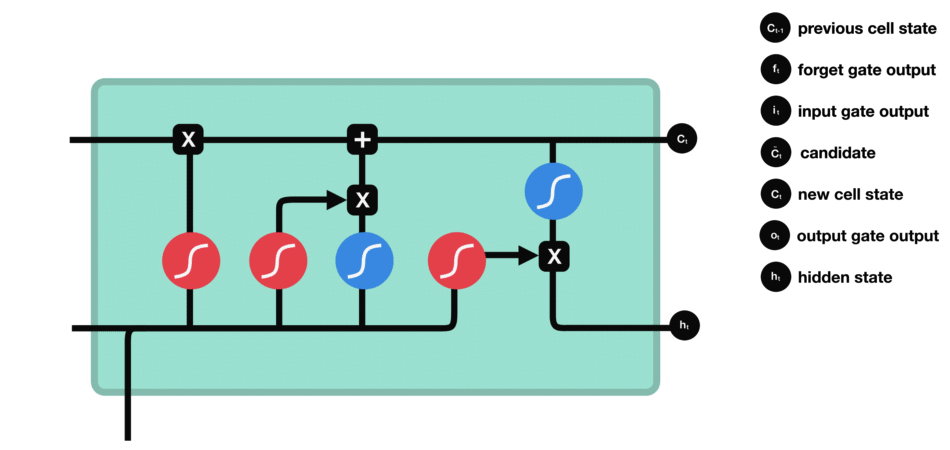
2.1 LSTM的模型结构
此处引用两张优质博主的示意图(初学阶段看后可“恍然大悟”,原文提及出处未提供链接,此处保留说明):

-
图1:LSTM整体结构拆解图

-
图2:LSTM细胞内部数据流向图
PyTorch中LSTM的参数说明
在PyTorch中调用LSTM需关注输入格式、实例化参数等,具体如下:
-
LSTM调用格式:
实际使用时,一般仅传入输入\(x\),初始隐藏状态\([h_{t-1}, c_{t-1}]\)可省略(默认自动初始化):output, (h_n, c_n) = lstm(x, [h_{t-1}, c_{t-1}])output:所有时间步的隐藏状态,维度为(seq_length, batch_size, hidden_size);h_n:最后一个时间步的隐藏状态,c_n:最后一个时间步的细胞状态。
-
输入\(x\)的维度:
注意:此维度顺序与常规“batch_first”习惯不同,需特别注意:
\(x: [seq\_length, batch\_size, input\_size]\)seq_length:时间步数量(序列长度);batch_size:批次大小;input_size:每个时间步的输入特征维度。
-
LSTM实例化参数:
lstm = nn.LSTM(input_size, hidden_size, num_layers)input_size:输入特征维度(与\(x\)的input_size一致);hidden_size:每个LSTM层的隐藏单元数量;num_layers:LSTM的堆叠层数(如“2”代表两层LSTM串联)。
2.2 LSTM相比RNN的优势
LSTM的反向传播推导较繁琐(涉及变量多),但能有效解决RNN的梯度问题,核心差异在于梯度传递机制:
- RNN的梯度问题:梯度是权重矩阵\(W\)的连乘(且\(W\)固定),最终形成指数函数——系数<1时梯度消失,系数>1时梯度爆炸;
- LSTM的梯度优化:梯度是对细胞状态\(C_t\)的偏导连乘——若前后记忆差异小,偏导值接近1,“多个1相乘”能稳定传递梯度;即使偶尔出现大偏导,也不会频繁发生(若序列前后无逻辑,本身无需训练)。
2.3 PyTorch实现LSTM对股票的预测(实战)
前置准备
需先安装金融数据集库tushare(用于获取股票数据),执行命令:pip install tushare。代码中关键步骤已添加详细注释。
完整代码
# -*- encoding: utf-8 -*-
import time
import datetime
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import tushare as tsclass LSTM_Regression(nn.Module):"""LSTM回归模型(用于股票价格预测)参数说明:- input_size: 输入特征维度(此处为“用于预测的历史天数”)- hidden_size: 隐藏层单元数量- output_size: 输出维度(默认1,单值预测:下一天收盘价)- num_layers: LSTM堆叠层数(默认2)"""def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):super().__init__()self.lstm = nn.LSTM(input_size, hidden_size, num_layers) # LSTM层self.fc = nn.Linear(hidden_size, output_size) # 全连接层(映射隐藏层输出到预测值)def forward(self, _x):"""前向传播参数:_x: 输入数据,维度(seq_length, batch_size, input_size)返回:预测值,维度(seq_length, batch_size, output_size)"""x, _ = self.lstm(_x) # LSTM输出:(seq_length, batch_size, hidden_size),忽略隐藏状态s, b, h = x.shape # 提取序列长度(s)、批次大小(b)、隐藏层维度(h)x = x.view(s * b, h) # 展平为(seq_length*batch_size, hidden_size),适配全连接层x = self.fc(x) # 全连接层输出:(seq_length*batch_size, output_size)x = x.view(s, b, -1) # 恢复维度:(seq_length, batch_size, output_size)return xdef create_dataset(data, days_for_train=5) -> (np.array, np.array):"""生成时序数据集:用前N天数据预测下1天数据参数:- data: 原始时序数据(如股票收盘价)- days_for_train: 输入序列长度(用前days_for_train天预测第days_for_train+1天)返回:- dataset_x: 输入数据集,维度(len(data)-days_for_train, days_for_train)- dataset_y: 输出数据集,维度(len(data)-days_for_train, 1)"""dataset_x, dataset_y = [], []for i in range(len(data) - days_for_train):_x = data[i:(i + days_for_train)] # 输入:前days_for_train天数据dataset_x.append(_x)dataset_y.append(data[i + days_for_train]) # 输出:第days_for_train+1天数据return np.array(dataset_x), np.array(dataset_y)if __name__ == '__main__':# 1. 配置与初始化DAYS_FOR_TRAIN = 5 # 用前5天数据预测第6天t0 = time.time() # 记录训练开始时间# 2. 数据获取与预处理# 获取上证指数(代码000001)收盘价,保存并读取data_close = ts.get_k_data('000001', start='2019-01-01', index=True)['close']data_close.to_csv('000001.csv', index=False) # 保存为CSVdata_close = pd.read_csv('000001.csv') # 读取数据# 补充获取上海证券交易所指数(可选)df_sh = ts.get_k_data('sh', start='2019-01-01', end=datetime.datetime.now().strftime('%Y-%m-%d'))# 数据类型转换与归一化(缩放到[0,1]区间,避免量级影响)data_close = data_close.astype('float32').valuesmax_val, min_val = np.max(data_close), np.min(data_close)data_close = (data_close - min_val) / (max_val - min_val)# 3. 划分训练集与测试集dataset_x, dataset_y = create_dataset(data_close, DAYS_FOR_TRAIN)train_size = int(len(dataset_x) * 0.7) # 70%数据用于训练,30%用于测试train_x, train_y = dataset_x[:train_size], dataset_y[:train_size]# 调整维度为LSTM输入格式:(seq_length, batch_size, input_size)train_x = train_x.reshape(-1, 1, DAYS_FOR_TRAIN) # batch_size=1,input_size=5train_y = train_y.reshape(-1, 1, 1) # 输出维度:(seq_length, 1, 1)# 转换为PyTorch张量train_x = torch.from_numpy(train_x)train_y = torch.from_numpy(train_y)# 4. 模型初始化与训练配置model = LSTM_Regression(DAYS_FOR_TRAIN, 8, output_size=1, num_layers=2) # 实例化模型# 计算模型总参数数量total_params = sum([param.nelement() for param in model.parameters()])print(f"Number of model parameters: {total_params / 1e6:.8f}M")loss_fn = nn.MSELoss() # 损失函数:均方误差(适用于回归任务)# 优化器:Adam,学习率1e-2optimizer = torch.optim.Adam(model.parameters(), lr=1e-2, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)# 5. 模型训练EPOCHS = 100 # 训练轮次(可根据需求调整)train_loss = [] # 记录每轮损失for epoch in range(EPOCHS):model.train() # 切换到训练模式pred = model(train_x) # 前向传播:获取预测值loss = loss_fn(pred, train_y) # 计算损失optimizer.zero_grad() # 清空梯度(避免累积)loss.backward() # 反向传播:计算梯度optimizer.step() # 更新模型参数train_loss.append(loss.item()) # 记录损失# 写入日志并打印训练信息with open('log.txt', 'a+') as f:f.write(f"Epoch: {epoch+1} - Loss: {loss.item():.5f}\n")if (epoch + 1) % 1 == 0: # 每1轮打印一次(可调整频率)print(f"Epoch: {epoch+1}, Loss: {loss.item():.5f}")# 6. 训练损失可视化plt.figure()plt.plot(train_loss, 'b', label='Train Loss')plt.title("Train Loss Curve")plt.ylabel("Loss")plt.xlabel("Epoch")plt.legend()plt.savefig('loss.png', format='png', dpi=200)plt.close()# 7. 训练时间统计t1 = time.time()total_time = (t1 - t0) / 60 # 转换为分钟print(f"The training time took {total_time:.2f} mins.")# 打印开始与结束时间start_time = time.asctime(time.localtime(t0))end_time = time.asctime(time.localtime(t1))print(f"The starting time was: {start_time}")print(f"The finishing time was: {end_time}")# 8. 模型评估与预测model.eval() # 切换到评估模式(禁用Dropout等)# 对全量数据预测(需填充前DAYS_FOR_TRAIN个值,使长度与原数据一致)dataset_x = dataset_x.reshape(-1, 1, DAYS_FOR_TRAIN)dataset_x = torch.from_numpy(dataset_x)pred_all = model(dataset_x) # 全量预测pred_all = pred_all.view(-1).data.numpy() # 展平为1D数组# 填充前DAYS_FOR_TRAIN个0(因前5天无历史数据,无法预测)pred_all = np.concatenate((np.zeros(DAYS_FOR_TRAIN), pred_all))assert len(pred_all) == len(data_close), "预测序列与原数据长度不匹配!"# 9. 预测结果可视化plt.figure()plt.plot(pred_all, 'r', label='Prediction') # 预测值(红色)plt.plot(data_close, 'b', label='Real Price')# 真实值(蓝色)plt.plot((train_size, train_size), (0, 1), 'g--') # 训练/测试分割线(绿色虚线)plt.legend(loc='best')plt.savefig('result.png', format='png', dpi=200)plt.close()# 可选:保存模型参数(供后续复用)# torch.save(model.state_dict(), 'model_params.pkl')

2.4 小问题:为什么采用tanh函数,不能都用sigmoid函数吗
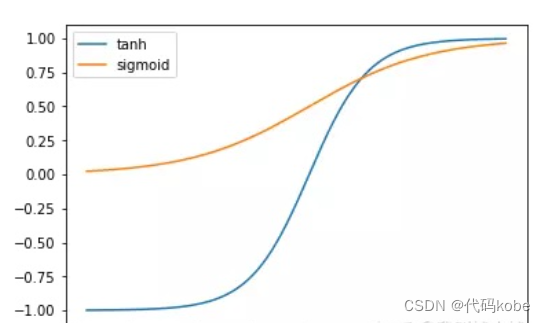
通过对比tanh与sigmoid的特性,可明确LSTM优先选择tanh的原因(原文提及函数图形,此处省略图形,聚焦核心差异):
| 对比维度 | sigmoid函数 | tanh函数 |
|---|---|---|
| 收敛速度 | 较慢(饱和速度慢) | 较快 |
| 值域范围 | (0, 1)(范围窄) | (-1, 1)(范围宽) |
| 输出均值 | ~0.5(非零均值) | ~0(零均值,便于处理) |
| 变化敏感区间 | 较窄(对输入变化不敏感) | 较宽(捕捉细节能力强) |
| 导数计算复杂度 | 需指数操作(\(\sigma(1-\sigma)\)) | 无需指数(\(1-tanh^2(x)\)) |
综上,tanh函数在收敛速度、数据处理便利性、计算效率上均优于sigmoid,因此LSTM中优先使用tanh函数(仅门控机制用sigmoid输出0-1权重)。
