DQN 变体(Rainbow)
双重 DQN(Double DQN)
在原始 DQN 中,经验回放与目标网络的引入使得 CNN 能够在强化学习中成功训练,但也带来了两个缺点:
- 学习速度显著降低,样本复杂度增高;
- 稳定性较差,不同运行结果可能不同。
@vanHasselt2015 提出了 Double DQN 以解决 Q 值的过估计(overestimation)问题。
在标准 DQN 中,目标值为:
由于 \(\max\) 操作,若某动作被高估,其 Q 值会被进一步放大,并传播至前面的状态。
@vanHasselt2010 证明这种高估在标准 Q-learning 中是必然的。
双重学习思想:使用两个网络——一个选择贪婪动作,另一个评估其 Q 值。
应用于 DQN 时,可直接利用已有的两个网络:
- 训练网络 \(\theta\):用于选择贪婪动作
\(a^* = \arg\max_{a'} Q_\theta(s', a')\) - 目标网络 \(\theta'\):用于评估该动作的 Q 值
目标更新为:
这一修改显著提升了性能与稳定性。
优先经验回放(Prioritized Experience Replay)
原始 DQN 的经验回放是均匀采样的,这意味着“无趣”样本与“重要”样本被选中的概率相同,浪费了训练资源。
@Schaul2015 提出优先经验回放(PER):按照 TD 误差大小优先采样。
采样概率为:
\(\alpha\) 控制采样强度。
这种机制更频繁地使用“出乎意料”的转移样本,从而加速学习。
对偶网络(Dueling Network)
在经典 DQN 中,一个网络直接预测所有动作的 Q 值:
但动作值由两部分组成:
- 状态本身的价值 \(V^\pi(s)\);
- 动作相对于该状态的优势(advantage) \(A^\pi(s,a)\)。
因此:
这种分解的好处:
- 在“坏状态”下(\(V(s)\) 低)无需探索每个动作;
- 优势函数的方差小于 Q 值,更易学习;
- 网络可更稳定地收敛。
@Wang2016 在 Double DQN + PER 框架中引入对偶结构(Dueling DQN):
为避免歧义(任意常数偏移),对优势进行归一化:
该结构在多数 Atari 游戏中显著优于 DDQN-PER。
分类 DQN(Categorical DQN / C51)
所有基于 Bellman 方程的 RL 方法都使用期望算子:
但这忽略了回报的方差。
@Bellemare2017 提出分布式 DQN(Distributional DQN):学习回报的概率分布而非均值。
假设回报范围为 \([V_\text{min},V_\text{max}]\),划分为 \(N\) 个离散点(原子)\(z_i\)。
网络输出每个原子的概率 \(p_i(s,a)\)(softmax 归一化):
则回报分布为:
对应的 Q 值即为其期望:
学习目标是最小化预测分布与 Bellman 更新分布间的 KL 散度:
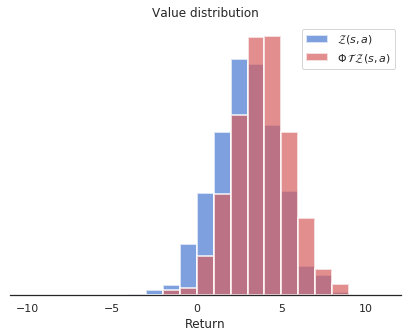
C51 在多数 Atari 游戏上优于 DQN,既提升性能又降低样本复杂度。
噪声 DQN(Noisy DQN)
传统 DQN 使用 \(\epsilon\)-greedy 或 softmax 探索机制,但这种全局噪声对所有状态一视同仁。
@Fortunato2017 提出在网络参数中注入噪声(参数噪声,Parameter Noise)。
假设参数服从高斯分布:
在每次前向传播时采样:
未访问状态的不确定性(\(\sigma_\theta\) 大)→ 更多探索;
已掌握状态的不确定性小 → 稳定利用。
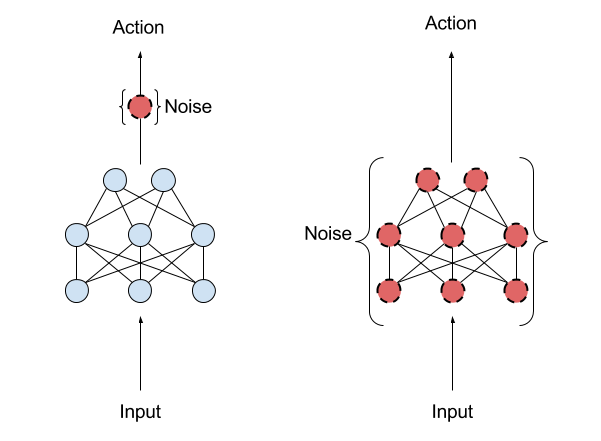
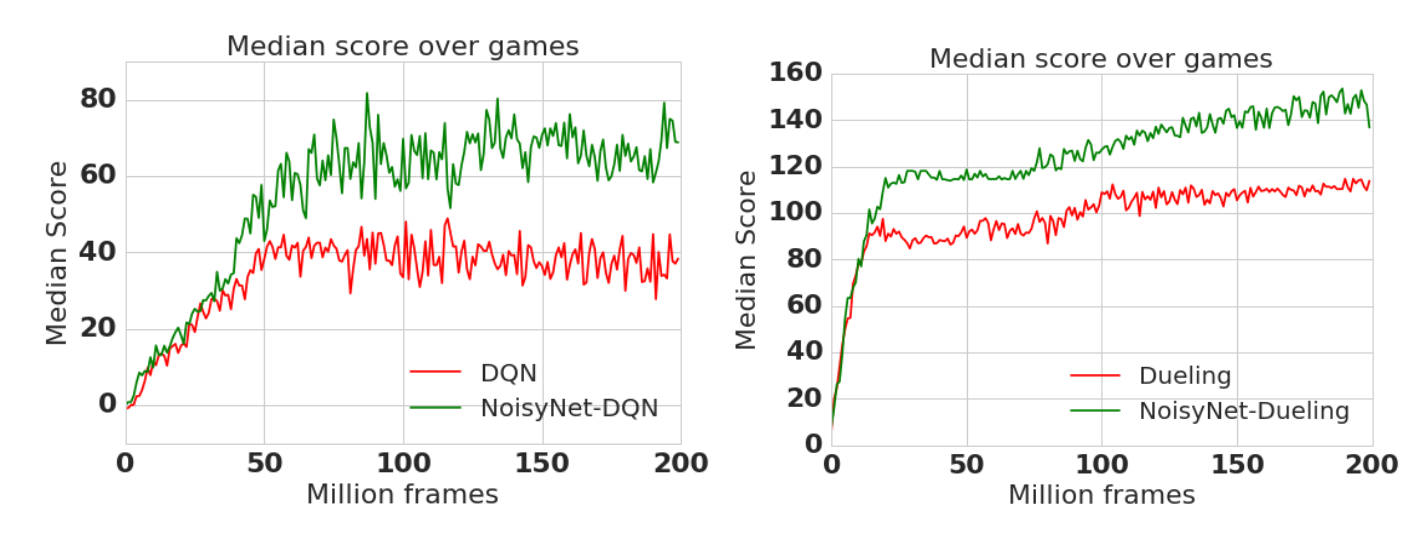
Noisy DQN 实现了自适应探索,无需额外调度,显著提升性能。
彩虹 DQN(Rainbow DQN)
DQN 经过多年发展,形成了多种增强版本:
| 改进方法 | 关键思想 |
|---|---|
| Double DQN [@vanHasselt2015] | 分离动作选择与评估,避免 Q 值过估计 |
| PER [@Schaul2015] | 按 TD 误差加权采样经验 |
| Dueling DQN [@Wang2016] | 拆分状态值与优势值学习 |
| Categorical DQN [@Bellemare2017] | 学习回报分布而非均值 |
| n-step Returns [@Sutton2017] | 融合未来 \(n\) 步回报以降低偏差 |
| Noisy DQN [@Fortunato2017] | 参数层面噪声,实现自适应探索 |
@Hessel2017 将上述方法整合成统一架构——Rainbow DQN。
其综合性能超过任一单独变体。
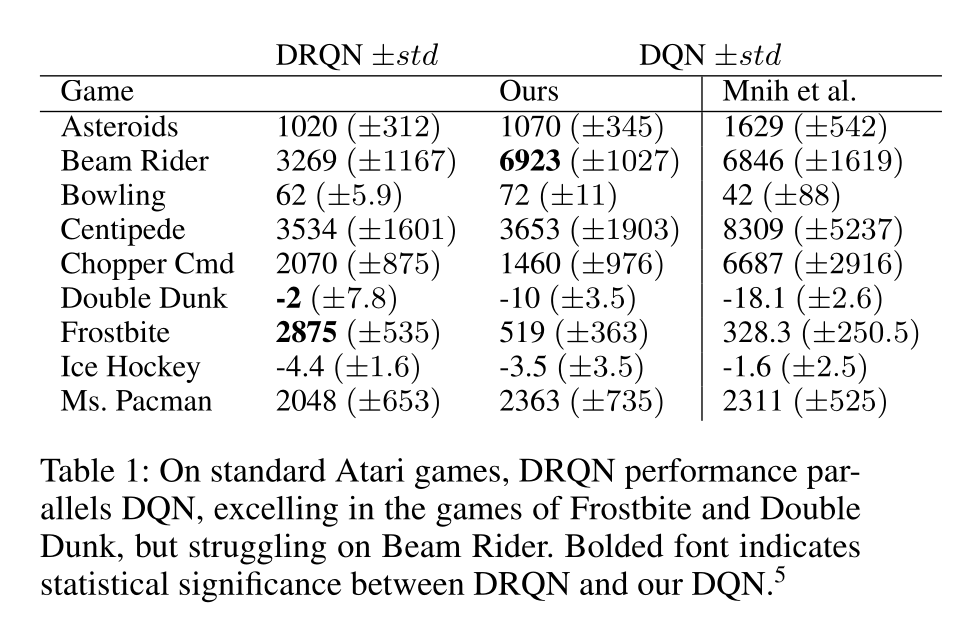
深度循环 Q-learning(DRQN)
Atari 游戏是部分可观测 MDP(POMDP):单帧缺乏速度等信息。
DQN 通过堆叠最近4帧缓解此问题,但仍存在局限:
- 存储消耗大;
- 无法捕捉长期依赖;
- 在需规划的任务(如 Montezuma’s Revenge)上表现差。
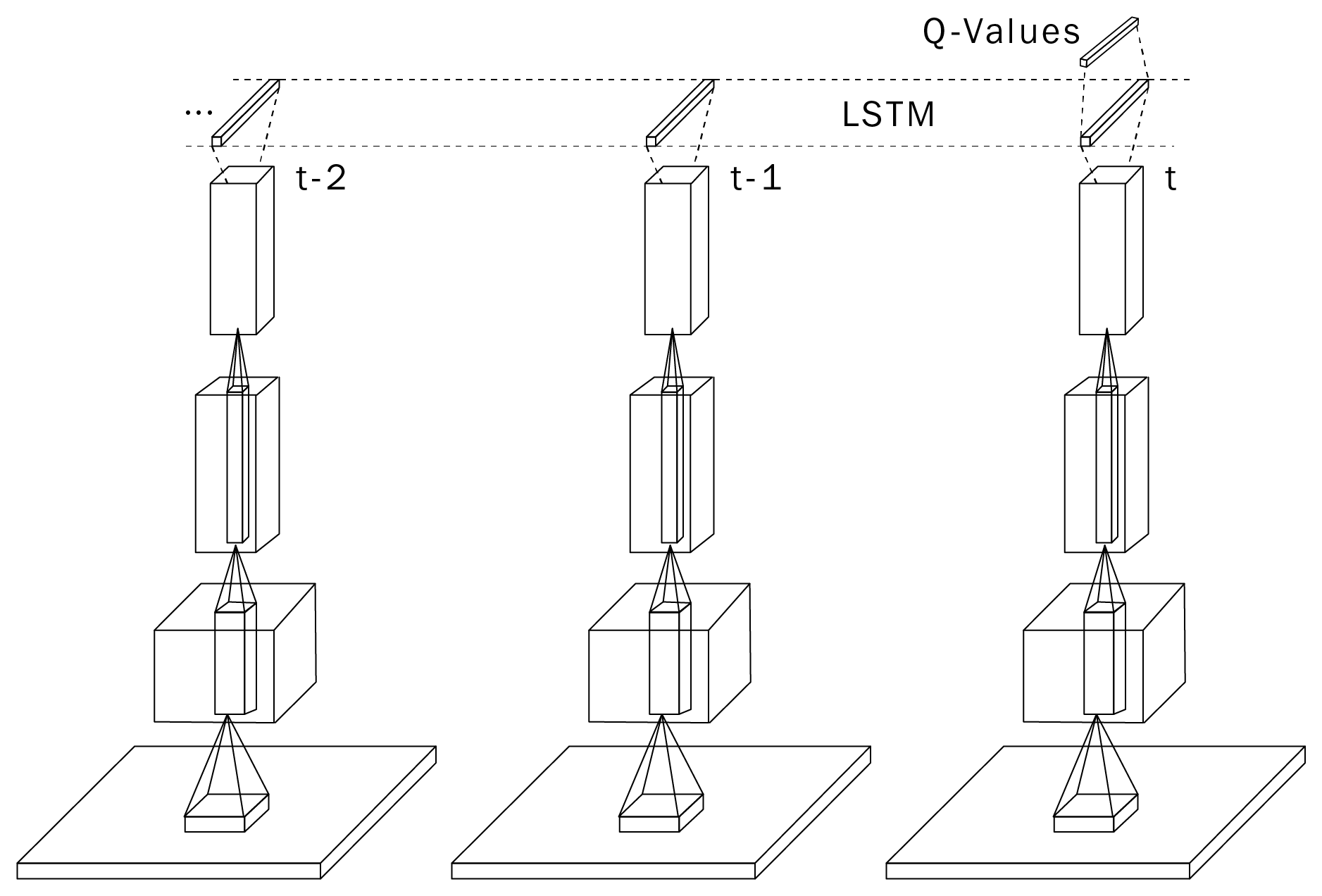
@Hausknecht2015 将 DQN 中的一层全连接层替换为 LSTM 层,输入为单帧,形成 DRQN。
LSTM 学习保留关键历史信息,从而更好地处理部分可观测任务。
但 LSTM 仍受限于截断反向传播(Truncated BPTT),无法学习超出截断长度的依赖,并显著增加训练时间。
尽管如此,DRQN 提供了一种更优雅的解决方案,让网络自行决定长期依赖的时间跨度。