T1 密码
原题链接
直接枚举修改区间暴力判断是 \(O(n^2)\)
原串很长,但修改操作是将区间变为其区间和,而对于 \(1e5\) 个数字,即使全取 \(9\),其和也不超过 \(6\) 位。
这启示我们在目标串上固定左端点,枚举最多长度为 \(6\) 的区间,表示为“期望通过修改得到的串”,保证两串的前缀与后缀相等时,判断原串中间部分的区间和是否与枚举得到的值相等即可,数据保证有解,放心大胆做即可。
点击查看代码
const int N=1e5+5;
string s,t,p;
int sums[N],a[N],n,R,m;
void xpigeon(){s=" ";cin>>t;n=t.size();s+=t;cin>>p;m=p.size();t=" ";t+=p;for(int i=1;i<=n;i++){a[i]=s[i]-'0';}for(int i=1;i<=n;i++){sums[i]=a[i]+sums[i-1];}while(s[n-R]==t[m-R]) R++;for(int l=1;l<=m && s[l-1]==t[l-1];l++){int tmp=0;for(int r=l;r<=min(m,l+6);r++){if(r>l && tmp==0) break;//前导0tmp=tmp*10+t[r]-'0';if (m-r<=R&& sums[n-m+r]==sums[l-1]+tmp){cout<<l<<" "<<n-m+r<<'\n';return ;}}}
}
T2 艺术家
原题链接
甚至是 STL 好题(?
从集合的角度去考虑,所有人一开始在同一个集合,每次操作相当于分裂,当集合大小为 \(1\) 时,一个艺术家唯一确定,但细想这种做法问题很多且无法解决,首先每次操作的艺术家有重叠,而且分裂的操作也并非好维护,我们把这个角度弃掉。
从出演状态的角度去考虑,一个艺术家能被确定,其演出安排须是所有人中唯一的,因为只有一件作品按照该方案演出,自然就对应得上了。
我们尝试用 \(01\) 串哈希的方式维护每个艺术家的出演状态,\(1\) 为出演,\(0\) 为没有,可以开一个 \(map\) 维护每一种哈希值对应的集合大小,每次操作时先删去原来的哈希,修改后再加入 \(map\),每一次操作过后统一判断这些哈希中集合大小为 \(1\) 的艺术家都有哪些。要注意修改一次哈希可能使得原来不唯一的哈希值变得唯一。
点击查看代码
const int N=1e5+5;
const ull base=2333;
int n,m,ans[N];
ull ha[N];
map<int,set<ull>>mp;
vector<int> to;
void xpigeon(){rd(n,m);memset(ans,0x3f,sizeof(ans));for(int i=1;i<=n;i++){mp[0].insert(i);}ull pw=1;for(int i=1,k;i<=m;i++){pw*=base;rd(k);to.clear();for(int j=1,a;j<=k;j++){rd(a);mp[ha[a]].erase(a);to.pb(ha[a]);ha[a]+=pw;mp[ha[a]].insert(a);to.pb(ha[a]);}for(auto x:to){if(mp[x].size()!=1) continue;auto it=*mp[x].begin();ans[it]=min(ans[it],i);mp[x].erase(it);}}for(int i=1;i<=n;i++){if(ans[i]==0x3f3f3f3f3f3f3f3f) cout<<0<<" ";else cout<<ans[i]<<" ";}
}
T3 度假
原题链接
若最终所有人同时覆盖的区间长度为 \(len\),显然长度越短越容易达成,我们考虑二分答案。
问题来到如何在固定的区间长度下寻找应该被覆盖的对应区间,设函数 \(f(x)\) 表示覆盖以 \(x\) 为左端点长度为 \(len\) 的固定区间的最小代价,\(g_i(x)\) 表示第 \(i\) 个区间覆盖以 \(x\) 为左端点区间长度为 \(len\) 的区间的最小代价,容易得到 \(g_i(x)\) 的函数方程:
不难发现这个函数是下凸的,把函数图像从前往家里那偷过来:
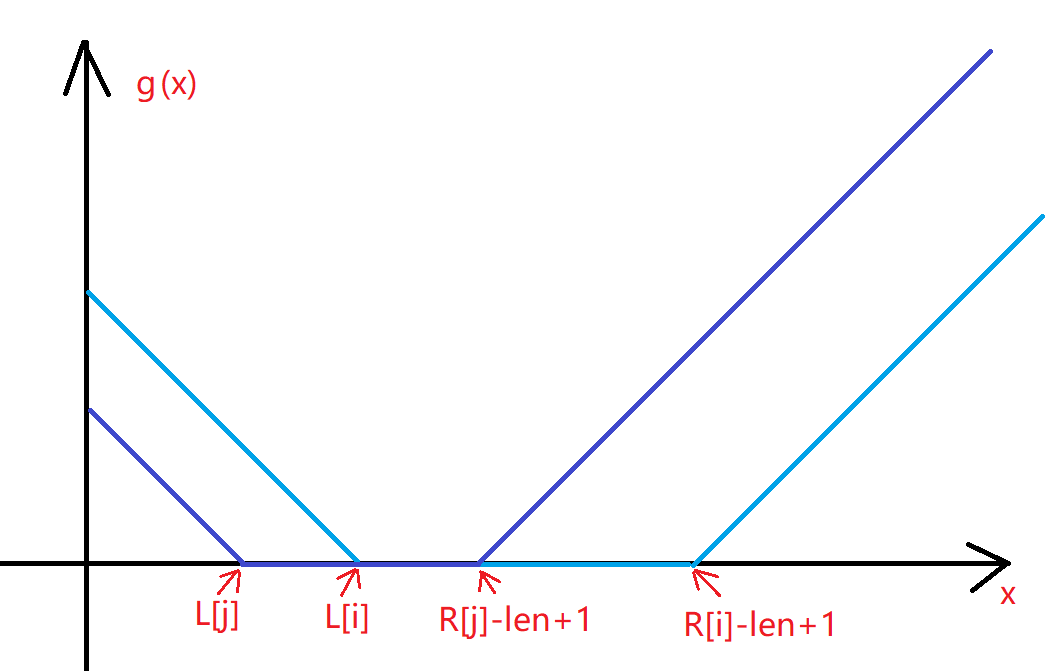
\(f(x)\) 的函数也偷过来:
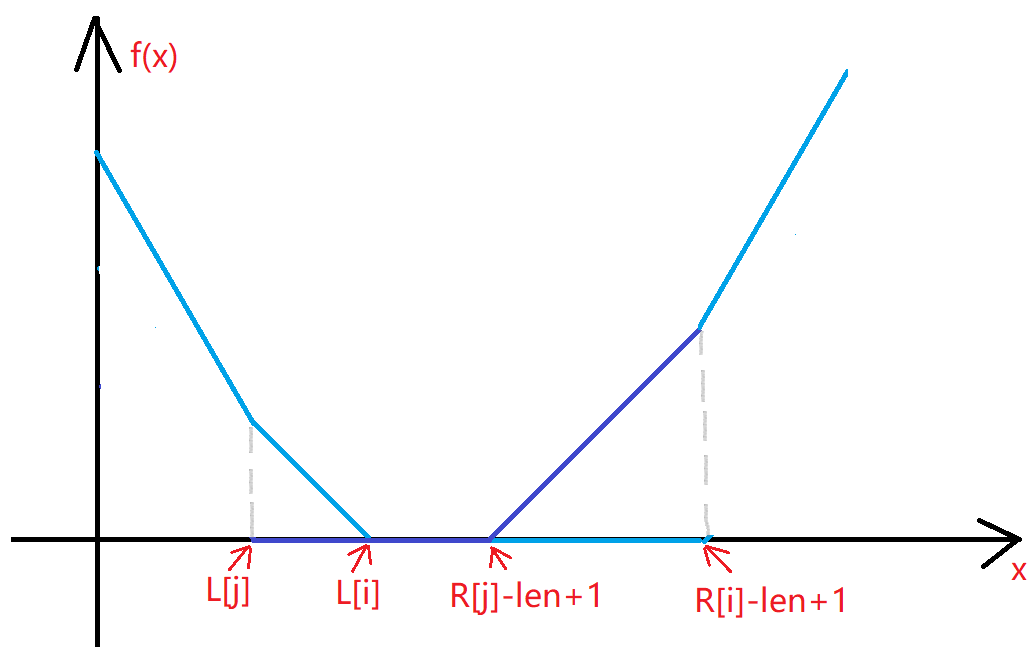
两个函数都是下凸的,说明最小值一定在转折点处取得,所以在二分前将左右端点排序,二分计算代价时枚举这些端点即可,代价计算时需要用前缀后缀和加双指针优化一下,方法写在注释里了。
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5e5+5;
int n,L[N],R[N];
ll K,pre[N],suf[N];
bool check(int k){for(int i=1,p=1;i<=n;i++){//[x,x+k-1]//找到第一个不满足 R<=x+k-1 的右端点while(p<=n && R[p]<=L[i]+k-1) p++;//x<=L部分的贡献if(suf[i]-1ll*(n-i+1)*L[i]+//R<=x+k-1 部分的贡献1ll*(L[i]+k-1)*(p-1)-pre[p-1] <=K ) return true;}for(int i=n,p=n;i>=1;i--){//枚举R-k+1作为左端点//找到第一个不满足 x<=L 的左端点while(p>=1 && L[p]>=R[i]-k+1) p--;if(suf[p+1]-1ll*(n-p)*(R[i]-k+1)+1ll*i*R[i]-pre[i]<=K) return true;}return false;
}
int plan_vacation(int _N, std::vector<int> _L, std::vector<int> _R, long long _K){n=_N,K=_K;int mn=1e9;for(int i=1;i<=n;i++){L[i]=_L[i-1],R[i]=_R[i-1];mn=min(mn,R[i]-L[i]+1);}sort(L+1,L+1+n),sort(R+1,R+1+n);for(int i=1;i<=n;i++){pre[i]=pre[i-1]+R[i];}for(int i=n;i>=1;i--){suf[i]=suf[i+1]+L[i];}int l=0,r=mn+1;while(r-l>1){int mid=(l+r)>>1;if(check(mid)) l=mid;else r=mid;}return l;
}
