| 难度 | 算法s | 日期 | 题目链接 |
|---|---|---|---|
| 普及− | DP | 2025-05-21 | https://luogu.com.cn/problem/P1044 |
因为本人 DP 很差,故撰此文巩固一下。
本文是对 P1044 [NOIP 2003 普及组] 栈 题解 的详细解释。
写的很直白了。。。几乎没有理解难度吧。。。
DP 状态设计
二维 DP 做法,\(dp[x][y]\) 表示:
- 有 \(x\) 个元素未入栈,意味着可以入栈 \(x\) 次。
- 有 \(y\) 个元素在栈内,意味着可以出栈 \(y\) 次。
(注意这里没有明确 \(dp[...][...]\) 表示什么,只是设计了状态,下面讲怎么设计 \(dp[...][...]\) 要表示的值。)
将这样转移:
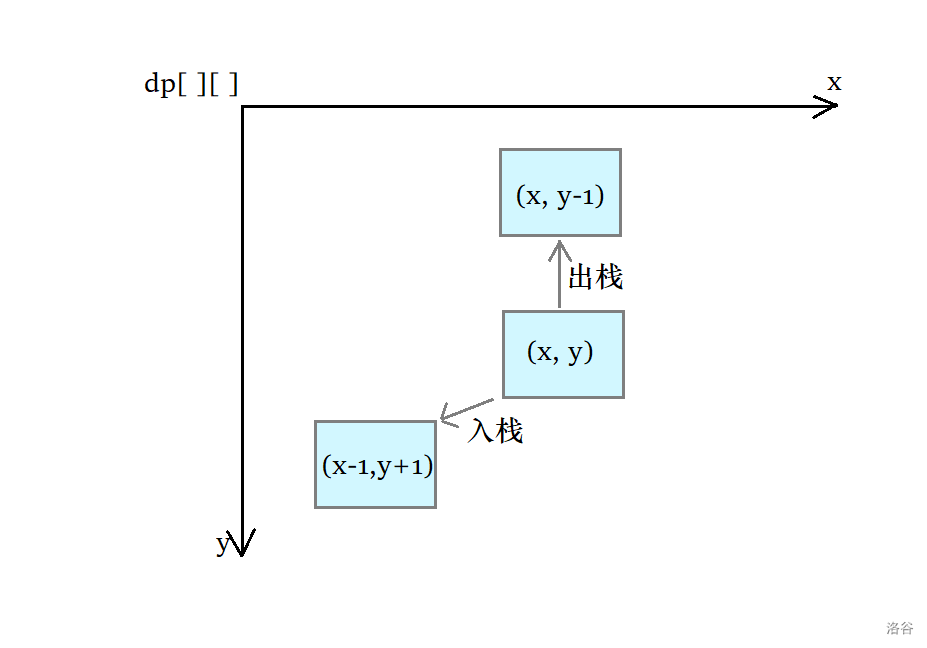
上图:“出入栈操作,状态转移过程”
然后呢?怎么算?
初始时,我们有一个状态 \(dp[n][0]\),也就是有 \(n\) 次入栈机会,但是从未执行过入栈操作。
接下来,我们进行操作, \(dp[x][y]\) 中 \(x\) 和 \(y\) 的值不断变化...
然后我们到达了一个末状态 \(dp[0][0]\),这时候我们没法进行更多操作了。
其实我们要计算的就是从初状态到末状态,有多少种“路径”,即所有可能的“操作序列”。
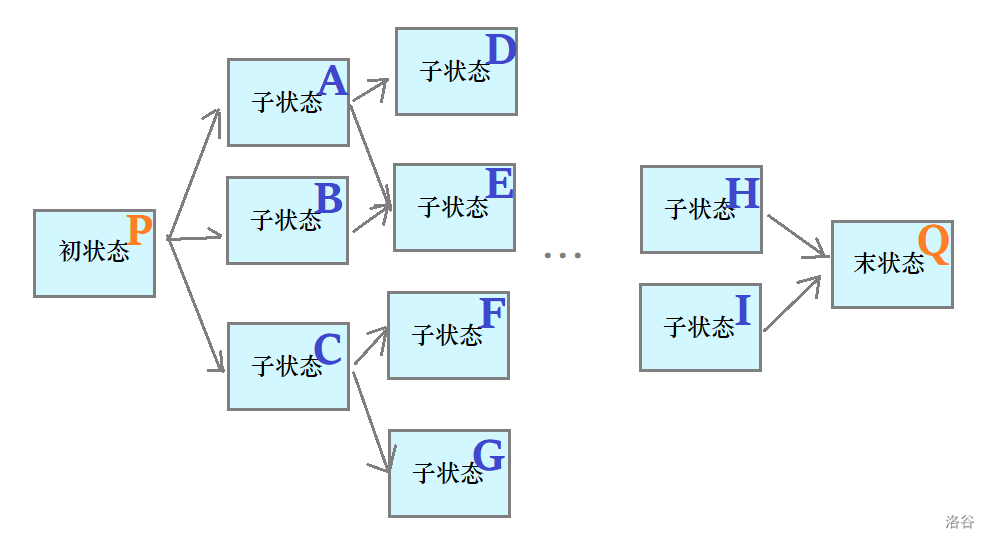
接下来我们要从末状态 \(Q\) 往回推,求可能的路径数。
很明显,从子状态 \(H\) 和 \(I\) 到末状态 \(Q\) 都只有一条路径。(边界状态)
现在来看这三个点:\(A\)、\(D\)、\(E\)。
很明显:
\(A\) 到末状态 \(Q\) 的路径数 \(=\) \(D\) 的路径数 \(+\) \(E\) 的路径数
归纳一下:
\(X\) 的路径数 \(=\) \(X\) 所有子状态的路径数之和
用这个公式从 \(Q\) 往回推,直到 \(P\) 就好了。
好,接下来DP。
决定了,\(dp[x][y]\) 就表示:还有 \(x\) 个元素要入栈,\(y\) 个元素要出栈,此时通向末状态可能的路径数。
(注意用词,这里用“还有...要”,暗示了最终要导向末状态 \(dp[0][0]\),必须把可以入栈的机会 \(x\) 和可以出栈的机会 \(y\) 都用完。)
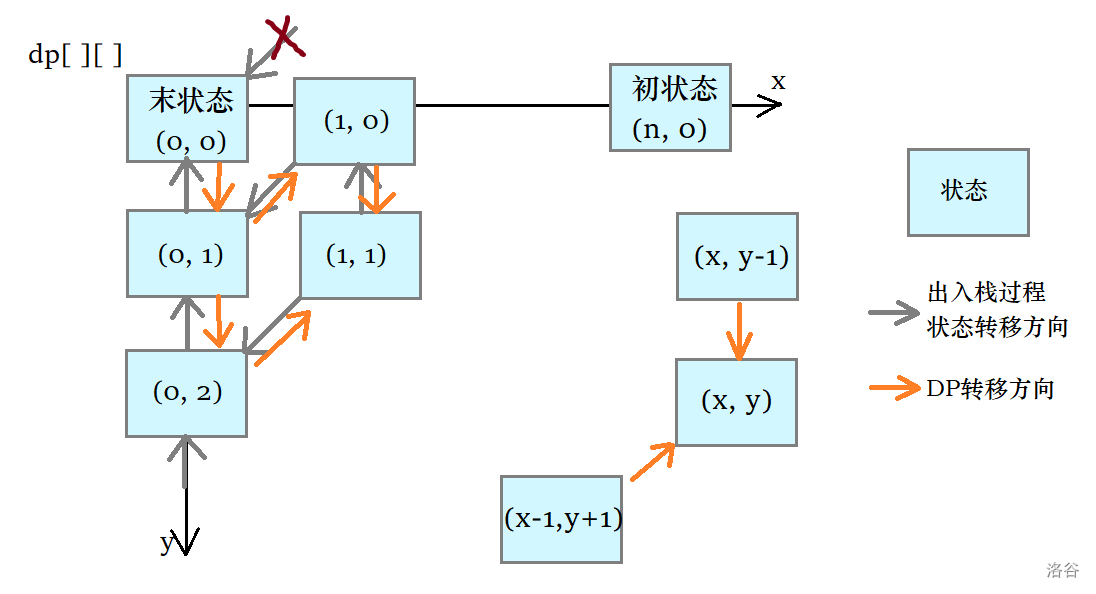
一图以蔽之。
之前我们不是推了“出入栈操作,状态转移过程”吗,其实 DP 的方向就是恰好相反。
很容易得到状态转移公式:
\(dp[x][y]=dp[x-1][y+1]+dp[x][y-1]\)
从图中还可以看出,先沿 \(x\) 遍历,然后跳到下一列 \(y\)。
代码(核心部分):
for (int x = 0; x <= n; x++) {for (int y = 0; y <= n; y++) {if (x == 0) {dp[x][y] = 1;} else if (y == 0) {dp[x][y] = dp[x - 1][y + 1];} else {dp[x][y] = dp[x][y - 1] + dp[x - 1][y + 1];}}}
[!important] 学到了什么?
对于这样一种问题:
给定初状态 \(P\),
可以进行 \(Op=\{...\}\) 种操作,每种操作会使当前状态转移到一个子状态。
求进行完所有操作后,可能的“操作路径”数。
那么我们用 DP 来解决问题,用反向推理的方法,其实 DP 转移方程很简单:
设计 DP 状态 \(dp(S)\)
(\(S\) 为状态,应该要包含各种在操作过程中会变化的量,比如要入栈的次数啊等等,写出来就是 \((x,y)\) 这样的式子)
\(dp(S)=\sum_i dp(S_i)\)
其中 \(S_i\) 表示从 \(S\) 可以进行到的子状态。
