跟标题一样有趣的计数题。
题意:很简单了,不再赘述。
做法:
首先看到这个至少一半,还要是 01 串,很容易想到先将 \(0\) 赋值为 \(-1\),\(1\) 赋值为 \(1\),那么 \(0, 1\) 至少一半就等于要求区间和 \(\le 0,\ge 0\)。
记 \(s_i\) 代表前 \(i\) 位赋值后的权值和。首先我们可以注意到,\(s_0,s_n\) 可以帮我们解决掉至少一种数。
-
\(s_0 = s_n\),那么所有的位置都可以选择区间 \([1,n]\) 解决。
-
\(s_0<s_n\),那么所有的 \(1\) 都可以选择 \([1,n]\) 解决。
-
\(s_0 > s_n\),那么所有的 \(0\) 都可以选择 \([1,n]\) 解决。
我们不妨假设 \(s_0 < s_n\),对于第二种我们把字符串全部反转一下就可以了。
那么现在就等于,令 \(A_i\) 代表所有满足第 \(i\) 位满足条件的字符串集合,求 \(|\bigcap\limits_{i=1}^n A_i|\)。
算这个很经典的是直接容斥,容斥转化为求补集的并,那么就等于我们现在钦定若干个点要求不可行,这些点会满足 \(\max\limits_{i=0}^{p-1}s_i<\min\limits_{i=p}^ns_i\)。
我们把 \(s\) 此时的图像画出来,就会变成这样:
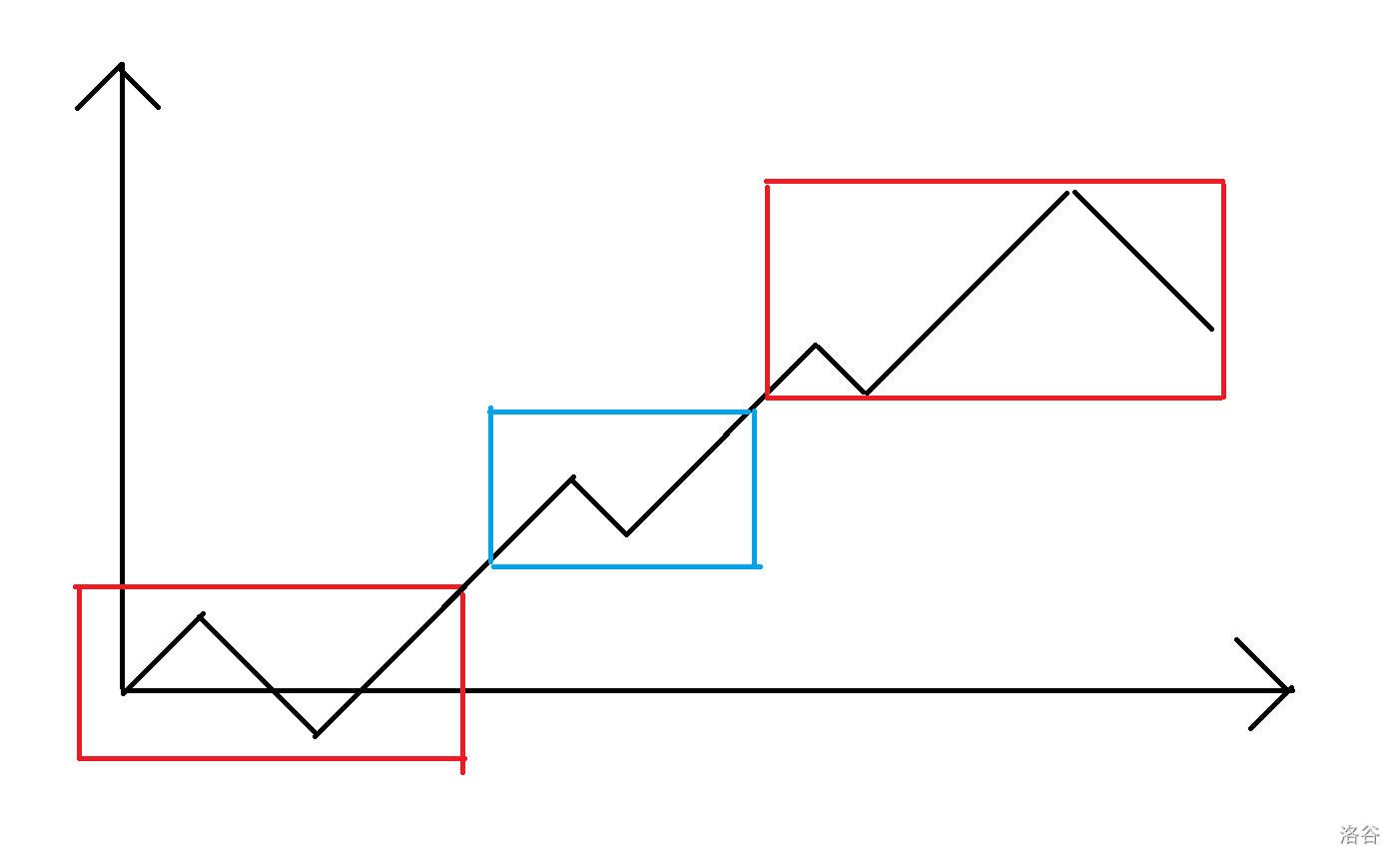
开头和结尾是红色段,中间会有若干个蓝色段,段和段之间都用 \(1\) 链接。
我们考虑限制,对于开头和结尾,只要最后/开头是最高的
/最低的就可以,因为他们其实是对称的,我们可以类似的计算。
我们记 \(f_i\) 代表走 \(i\) 步,只要不越过 \(x\) 轴就可以,即不碰到 \(y=-1\)。
枚举分配 \(x\) 次向下,然后反射一次计算,方案数是 \(\binom{n}{x}-\binom{n}{x-1}\),加总,可以得到 \(f_i = \binom{n}{\frac n 2}\)。
然后我们考虑中间的蓝色段,要求开头,结尾分别是最小值和最大值,记长度为 \(i\) 的答案为 \(g_i\)。
首先我们先不思考复杂度,我们直接考虑枚举最后到了 \(y=k\) 的位置,然后就等于说我这个路径不能经过 \(y=k+1,y=-1\),直接反射容斥可以做,单次求解一个 \(g_i\) 的复杂度是 \(O(n\log n)\),总复杂度还要乘上一个 \(n\)。
但是我们发现一个事情,无论我们的 \(n\) 长成什么样,我们的反射容斥过程是不变的,所以我们可以把答案记为 \(\sum\limits_{i} h_iv_i\),其中 \(h\) 是反射容斥的系数,可以直接提前枚举 \(y=k\) 然后总复杂度 \(O(n\log n)\) 计算完;\(v\) 是从 \((0,0)\) 走到 \((n, i)\) 的方案数。
我们把 \(v\) 用多项式的方式写开,注意到 \((n,i),(n,-i)\) 的方案数是一样的,在下面展开会用到,就变成了:
然后我们发现,这个东西就等于 \([x^0]H(x+x^{-1})^n\),其中 \(H\) 是 \(h\) 的生成函数。
那么我们有了 \(H\),现在就可以用分治算出来所有的 \(g\)。
具体的,我们可以分治去计算,考虑当前计算到 \([l,r]\),我们先递归左侧,再将多项式乘上 \((x+x^{-1})^{mid-l+1}\) 再递归到右侧。但是这样有个问题,多项式长度太长了,显然不能乘那么多次,但是我们注意到,对于一个区间内,最多乘上的是 \((x+x^{-1})^{r-l}\),所以我们只用留下来 \([l-r,r-l]\) 次的多项式就可以了,这样复杂度就是有保证的 \(O(n\log^2n)\)。
但是还没做完,我们还要把原题的容斥解决,考虑 dp,有转移式:
直接分治 NTT 解决即可,记得最后对于每个 \(i\) 还要乘上 \(f_{n-i}\) 拼上最后一段,同时这些 dp 值仅对字符串第 \(i\) 位为 \(0\) 生效。
代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 6e5 + 5, mod = 998244353, gb = 3, gi = (mod + 1) / gb;
int rev[maxn];
void init(int len) {for (int i = 1; i < len; i++) {rev[i] = rev[i >> 1] >> 1;if(i & 1)rev[i] |= (len >> 1); }
}
int qpow(int x, int k, int p) {int res = 1;while(k) {if(k & 1)res = res * x % p;x = x * x % p, k >>= 1;}return res;
}
clock_t st = clock();
struct Poly {vector<int> a;void resize(int N) {a.resize(N);}int size() {return a.size();}int& operator[](int x) {return a[x];}void NTT(int f) {int n = size();for (int i = 0; i < n; i++)if(i < rev[i])swap(a[i], a[rev[i]]);for (int h = 2; h <= n; h <<= 1) {int d = qpow((f == 1 ? gb : gi), (mod - 1) / h, mod);int cnt = 0;for (int i = 0; i < n; i += h) {int nw = 1;for (int j = i; j < i + h / 2; j++) {int a0 = a[j], a1 = a[j + h / 2] * nw % mod;cnt++;a[j] = (a0 + a1) % mod, a[j + h / 2] = (a0 - a1 + mod) % mod;nw = nw * d % mod;}}if(cnt > n)cout << cnt << endl;// if(n > 200000)// cout << h << " " << cnt << " " << (double)(clock() - st) / CLOCKS_PER_SEC << endl;}if(f == -1) {int inv = qpow(n, mod - 2, mod);for (int i = 0; i < n; i++)a[i] = a[i] * inv % mod;}}void print() {for (int i = 0; i < size(); i++)cout << a[i] << " ";cout << endl;}friend Poly operator*(Poly f, Poly g) {int len = 1, t = f.size() + g.size() - 1;while(len < t)len <<= 1;// cout << endl;// f.print(), g.print();f.resize(len), g.resize(len);init(len), f.NTT(1);// if(t > 100000)// cout << (double)(clock() - st) / CLOCKS_PER_SEC << endl;g.NTT(1);for (int i = 0; i < len; i++)f[i] = f[i] * g[i] % mod;f.NTT(-1);f.resize(t);// f.print();return f;}
} ;
int jc[maxn], revjc[maxn], n, f[maxn], g[maxn], dp[maxn];
string s;
void prepare() {jc[0] = revjc[0] = revjc[1] = 1;for (int i = 1; i <= n; i++)jc[i] = jc[i - 1] * i % mod;for (int i = 2; i <= n; i++)revjc[i] = (mod - mod / i) * revjc[mod % i] % mod;for (int i = 2; i <= n; i++)revjc[i] = revjc[i] * revjc[i - 1] % mod;
}
inline int C(int m, int n) {if(m < 0 || n < 0 || m < n)return 0;return jc[m] * revjc[n] % mod * revjc[m - n] % mod;
}
void solveseg(int l, int r, Poly &nw) {if(l == r) {g[l] = nw[0];// if(l && l % 10000 == 0)// cout << l << " " << (double)(clock() - st) / CLOCKS_PER_SEC << endl;// cout << l << " " << g[l] << endl;return ;}int mid = l + r >> 1;Poly cur; cur.resize(2 * (mid - l) + 1);for (int i = 0; i <= 2 * (mid - l); i++)cur[i] = nw[i + r - mid];solveseg(l, mid, cur);
// if(l == 0 && r == 100000)// cout << (double)(clock() - st) / CLOCKS_PER_SEC << endl;Poly f, g; f.resize(2 * (r - l) + 1);g.resize(2 * (mid - l + 1) + 1);for (int i = 0; i <= 2 * (r - l); i++)f[i] = nw[i];for (int i = 0; i <= 2 * (mid - l + 1); i++) {if(i & 1)g[i] = 0;elseg[i] = C(mid - l + 1, i / 2);}
// cout << l << " " << r << endl;
// if(l == 0 && r == 100000)// cout << (double)(clock() - st) / CLOCKS_PER_SEC << endl;f = f * g;cur.resize(0), cur.resize(2 * (r - mid - 1) + 1);for (int i = 0; i <= 2 * (r - mid - 1); i++)cur[i] = f[i + 2 * (mid - l + 1)];solveseg(mid + 1, r, cur);
}
int ans;
void solve(int l, int r) {if(l == r) {if(s[l] == '1')return ;dp[l] = (f[l - 1] - dp[l] + mod) % mod;ans = (ans + dp[l] * f[n - l]) % mod;// cout << l << " " << dp[l] << endl;return ;}int mid = l + r >> 1;solve(l, mid);Poly F, G; F.resize(mid - l + 1), G.resize(r - l + 1);for (int i = 0; i <= mid - l; i++) {if(s[l + i] == '0')F[i] = dp[i + l];elseF[i] = 0;}for (int i = 0; i <= r - l; i++) G[i] = g[i];F = F * G;for (int i = mid + 1; i <= r; i++)if(s[i] == '0')dp[i] = (dp[i] + F[i - l - 1]) % mod;solve(mid + 1, r);
}
signed main() {ios::sync_with_stdio(false);cin >> n >> s; s = ' ' + s;prepare();for (int i = 0; i <= n; i++)f[i] = C(i, i / 2);Poly f; f.resize(2 * n + 1);for (int k = 0; k <= n; k++) {f[n + k] = (f[n + k] + 1) % mod;int x = -2 - k, y = k + 2, cur = 0;while(abs(x) <= n || abs(y) <= n) {if(cur == 0) {if(abs(x) <= n)f[n + x] = (f[n + x] - 1) % mod;if(abs(y) <= n)f[n + y] = (f[n + y] - 1) % mod;x = 2 * k + 2 - x; y = -2 - y;}else {if(abs(x) <= n)f[n + x] = (f[n + x] + 1 + mod) % mod;if(abs(y) <= n)f[n + y] = (f[n + y] + 1 + mod) % mod;x = -2 - x, y = 2 * k + 2 - y;}cur ^= 1;}}
// f.print();solveseg(0, n, f);
// cout << 123 << endl;solve(1, n);
// cout << ans << endl;for (int i = 1; i <= n; i++)s[i] = '0' + '1' - s[i];solve(1, n);int bs = 1;for (int i = 1; i <= n; i++)bs = bs * 2 % mod;
// cout << ans << endl;cout << (bs - ans + mod) % mod << endl;return 0;
}
