当前位置：首页 > news >正文

二分图/忆re.

news 2025/10/23 21:10:29

rt：
本文分两部分

二分图
忆re.

part 1 二分图

定义

我会告诉你我OIwiki没看懂吗？

其实就是有一张图，将它的点分为红点和蓝点，红点只能和蓝点相连，同理蓝点只能和红点相连，满足这个条件的图就是二分图。

形式上的：

（还是贺了OIwiki）

判定

（没太用过）
给这张图染色，若直接相连的两个点颜色是相同的，则其不是一个二分图。（即如定义所述）

代码

#include<bits/stdc++.h>
using namespace std;
int color[1010];
int h[1010],to[20010],nxt[20010],tot;
void add(int x,int y)
{tot++;to[tot]=y;nxt[tot]=h[x];h[x]=tot; 
}
bool dfs(int x,int c) 
{color[x] = c; // 给当前节点染色for(int i=h[x];i;i=nxt[i]){int y=to[i];if(color[y]==c) {return false; // 相邻节点颜色相同，不是二分图}if(color[y]==0&&!dfs(y,-c)) {return false; // 未染色，递归染色}}return true;
}
int main() 
{int n,m;cin>>n>>m;memset(color,0,sizeof(color));for(int i=1;i<=m;i++) {int x,y;cin>>x>>y;add(x,y);add(y,x);   }bool is=true;for (int i=1;i<=n;i++) {if(color[i]==0&&!dfs(i,1)) {is=false;break;}}cout<<is<<endl;return 0;
}

二分图最大匹配

定义

二分图匹配的例子是\(p,t\)配对。设有若干\(t\)和\(p\)，每个只能配对一次，且允许配对的组合已由某个列表限定。此时，二分图最大匹配算法的任务就是在这些限制下，找到最多的配对对数，使尽可能多的成功配对。

匈牙利算法

rt:
我们有这样一张二分图；

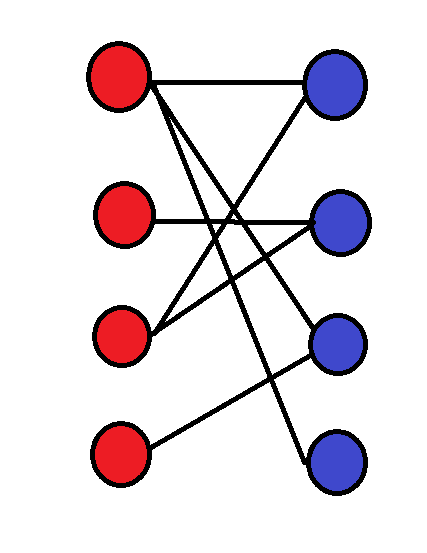
让第一个红点先匹配：

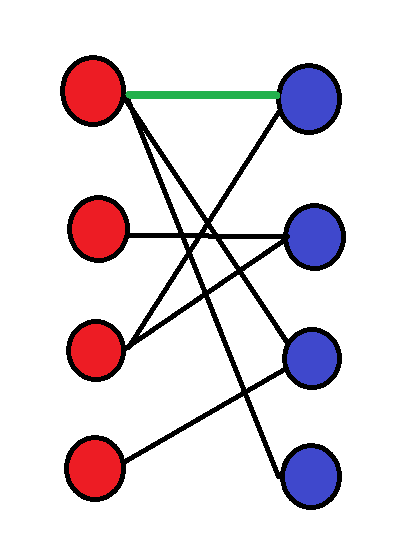
然后匹配第二个红点：

发现第三个红点没有可以匹配的了，让一个红点给它让位：

最后第四个红点也需要一个红点给他让位：

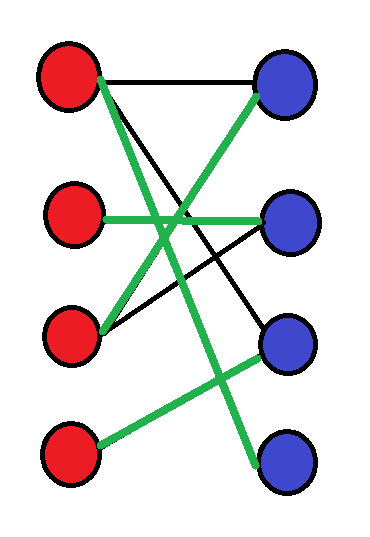
都匹配上了，最大匹配数是\(4\)

例题

洛谷 P3386 【模板】二分图最大匹配

代码实现

#include<bits/stdc++.h>
using namespace std;
int match[1010];
bool vis[1010];
int h[1010],to[50010],nxt[50010],tot;
void add(int x,int y)
{tot++;to[tot]=y;nxt[tot]=h[x];h[x]=tot;
}
bool Hungarian(int x)
{for(int i=h[x];i;i=nxt[i]){int y=to[i];if(!vis[y]){vis[y]=1;if(!match[y]||Hungarian(match[y])){match[y]=x;return 1;}}	}	return 0;
} 
int main()
{int n,m,e;cin>>n>>m>>e;for(int i=1;i<=e;i++){int x,y;cin>>x>>y;add(x,y);}int ans=0;for(int i=1;i<=n;i++){memset(vis,false,sizeof(vis));if(Hungarian(i)){ans++;}}cout<<ans;return 0;
}