最近接触了 GPU 编程,尝试了用 CUDA 写一些并行计算案例,拿了矩阵乘法作为第一个练手项目。
过去的经验让我误以为这东西很 naive,但其实从并行的角度看,会发现很多串行思维所没有机会接触的细节——总体而言,虽然遇到不少困难,但还是觉得收获丰富。
矩阵乘法的实现优化有非常多的方法,这里只是简单尝试了粗浅的几种,其实后面还有很多优化分支,但是打算日后再做研究。
CPU 矩阵乘法
直接实现是 \(O(NMK)\),无需多言。
Naive GPU 矩阵乘法
考虑对于每一组 \((i,j)\),计算 \(c_{i,j}\) 需要遍历一次下标 \(k\),而每个 \((i,j)\) 之间都是互相独立的。因此简单考虑,使用 \(O(N^2)\) 个线程(thread),然后对每个 thread 指定一个 \(O(K)\) 遍历下标 \(k\) 的任务。
这样计算花费是 \(O(K)\),但是由于每次访问的都是 global memory,总共会有 \(3MNK\) 次访问,会比较慢。
矩阵分块
这部分参考了 CUDA SGEMM矩阵乘法优化笔记——从入门到cublas - 知乎 的思路。
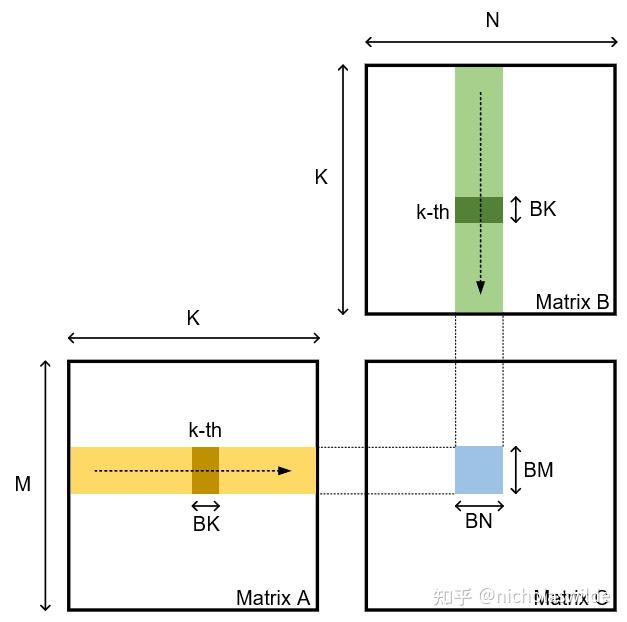
核心是将某一块 A/B 从 global memory 转移到 block 的 shared memory 中。
如果按如下分块,一次 \(BN\times BM\) 的 C 子矩阵的计算,会一次性将 A 和 B 两个块从 global memory 载入一遍,然后计算 C 中的值就不用访问 global memory。最终 global memory 的总访问次数会除以 \(BK\)。
不过 \(BK\) 太大不行,shared memory 存在硬件限制。
const int BM = 128;
const int BN = 128;
const int BK = 8;
const int TM = 8;
const int TN = 8;__global__
void tiledMatmul(float* A, float* B, float* C, int M, int K, int N) {const int bx = blockIdx.x;const int by = blockIdx.y;const int tx = threadIdx.x;const int ty = threadIdx.y;const int tid = tx + ty * blockDim.x;__shared__ float s_a[BM][BK];__shared__ float s_b[BK][BN];float r_c[TM][TN] = {0.0};// ???int load_a_smem_m = tid >> 1;int load_a_smem_k = (tid & 1) << 2;int load_b_smem_k = tid >> 5;int load_b_smem_n = (tid & 31) << 2; int load_a_gmem_m = by * BM + load_a_smem_m;int load_b_gmem_n = bx * BN + load_b_smem_n;for (int bk = 0; bk < (K + BK - 1) / BK; bk++) {int load_a_gmem_k = bk * BK + load_a_smem_k;int load_b_gmem_k = bk * BK + load_b_smem_k;int load_a_gmem_addr = load_a_gmem_m * K + load_a_gmem_k;int load_b_gmem_addr = load_b_gmem_k * N + load_b_gmem_n;FLOAT4(s_a[load_a_smem_m][load_a_smem_k]) = FLOAT4(A[load_a_gmem_addr]);FLOAT4(s_b[load_b_smem_k][load_b_smem_n]) = FLOAT4(B[load_b_gmem_addr]);__syncthreads();#pragma unrollfor (int k = 0; k < BK; k++) {#pragma unrollfor (int m = 0; m < TM; m++) {#pragma unrollfor (int n = 0; n < TN; n++) {int comp_a_smem_m = ty * TM + m;int comp_b_smem_n = tx * TN + n;r_c[m][n] += s_a[comp_a_smem_m][k] * s_b[k][comp_b_smem_n];}}}__syncthreads();}#pragma unrollfor (int i = 0; i < TM; i++) {int store_c_gmem_m = by * BM + ty * TM + i;#pragma unrollfor (int j = 0; j < TN; j += 4) {int store_c_gmem_n = bx * BN + tx * TN + j;int store_c_gmem_addr = store_c_gmem_m * N + store_c_gmem_n;FLOAT4(C[store_c_gmem_addr]) = FLOAT4(r_c[i][j]);}}
}int main() {// ...dim3 blockSize(BN / TN, BM / TM);dim3 gridSize(ceil(N, BN), ceil(M, BM));// ...
}
实现也是参考的上面,但是打问号的位置看了一天才搞明白。。。
其实就是 load 和计算两个过程,是一堆 thread 先把要求的位置都 load 上,然后大家对齐进度(__syncthreads()),然后开始计算。而 load 过程只要保证不重不漏,而不必和后面的计算有直接对应关系,也不用讲究顺序。而(每次 bk 的循环体)load 的(其中一个矩阵)浮点数个数刚好等于 thread 个数,那么就找个一一对应关系即可。于是有了上面代码看起来很简洁但不太直观的写法。如果 BM/BN 等参数改变,可能还会多写一组循环。
Tensor Core 使用尝试 1:WMMA
使用了 \(16\times 16\times 16\) 的 FP16 \(\to\) FP32 WMMA(Warp-level Matrix Multiply Accumulate)接口。
这里有一个误区,那就是只要块长设置成 16 或 16 的倍数就行。但是 tensor core 是 warp 层的操作,一个 warp 包含的 32 个 thread 协同工作才能操作 tensor core。
也就是说不能直接在核函数中指定一个 \(16\times 16\times 16\) 的朴素矩阵乘法,然后直接改成 tensor core。
考虑重新组织计算结构:
const int WMMA_M = 16;
const int WMMA_N = 16;
const int WMMA_K = 16;const int BM = 128;
const int BN = 128;
const int BK = 16;const int WARP_SIZE = 32;
const int WARPS_PER_BLOCK_M = 4; // BM / WARP_SIZE
const int WARPS_PER_BLOCK_N = 4; // BN / WARP_SIZEint main() {// ...const int WARPS_PER_BLOCK = WARPS_PER_BLOCK_M * WARPS_PER_BLOCK_N; // 16dim3 blockDim(WARPS_PER_BLOCK * WARP_SIZE /* 16*32 */ );dim3 gridDim((N + BN - 1) / BN, (M + BM - 1) / BM);// ...
}
这里将 \(BK\) 调整为 16,适应 WMMA 的尺寸,\(BM,BN\) 保持不变。
每个 block 设定为 \(16\times 32\) 大小,内含 16 个 warp,行、列方向为 \(4\times 4\)。
对于每个 warp,在计算过程中分管 \(32\times 32\) 的区域,也就是说四组 WMMA。示意图:

计算部分的代码:
__global__ void tensorCoreMatmul(half* A, half* B, float* C, int M, int K, int N) {__shared__ half s_a[BM][BK];__shared__ half s_b[BK][BN];const int warpId = threadIdx.x / WARP_SIZE;const int warpM = warpId / WARPS_PER_BLOCK_N;const int warpN = warpId % WARPS_PER_BLOCK_N;const int warpRowOffset = warpM * WMMA_M * 2;const int warpColOffset = warpN * WMMA_N * 2;const int blockRowOffset = blockIdx.y * BM;const int blockColOffset = blockIdx.x * BN;wmma::fragment<wmma::accumulator, WMMA_M, WMMA_N, WMMA_K, float> acc[2][2];#pragma unrollfor (int i = 0; i < 2; i++) {#pragma unrollfor (int j = 0; j < 2; j++) {wmma::fill_fragment(acc[i][j], 0.0f);}}for (int bk = 0; bk < K; bk += BK) {// ... loading data ...__syncthreads();wmma::fragment<wmma::matrix_a, WMMA_M, WMMA_N, WMMA_K, half, wmma::row_major> a_frag;wmma::fragment<wmma::matrix_b, WMMA_M, WMMA_N, WMMA_K, half, wmma::row_major> b_frag;#pragma unrollfor (int k = 0; k < BK; k += WMMA_K) {#pragma unrollfor (int i = 0; i < 2; i++) {#pragma unrollfor (int j = 0; j < 2; j++) {int aRow = warpRowOffset + i * WMMA_M;int aCol = k;int bRow = k;int bCol = warpColOffset + j * WMMA_N;wmma::load_matrix_sync(a_frag, &s_a[aRow][aCol], BK);wmma::load_matrix_sync(b_frag, &s_b[bRow][bCol], BN);wmma::mma_sync(acc[i][j], a_frag, b_frag, acc[i][j]);}}}__syncthreads();}// write results back to global memory.#pragma unrollfor (int i = 0; i < 2; i++) {#pragma unrollfor (int j = 0; j < 2; j++) {int cRow = blockRowOffset + warpRowOffset + i * WMMA_M;int cCol = blockColOffset + warpColOffset + j * WMMA_N;if (cRow < M && cCol < N) {wmma::store_matrix_sync(&C[cRow * N + cCol], acc[i][j], N, wmma::mem_row_major);}}}
}然后考虑怎么把数据加载到 shared memory 里。
对于每个 block,其中每个 \(bk (0\le bk<\frac {K}{BK})\),涉及到的 A 矩阵有 \(BM\times BK = 2048\) 个 half,B 有 \(BK\times BN=2048\) 个。也就是说一个 thread 要 load \(2048/(32\times 16) = 4\) 个 A 的 half,B 同理。
把四个 half 打包了,一句话搞定:
// 加载 A 矩阵: s_a[128][16]{int load_idx = threadIdx.x; // 0-511int row = load_idx / 4; // 0-127 (BK/4 = 16/4 = 4)int col = (load_idx % 4) * 4; // 0, 4, 8, 12int globalRow = blockRowOffset + row;int globalCol = bk + col;HALF4(s_a[row][col]) = HALF4(A[globalRow * K + globalCol]);}// 加载 B 矩阵: s_b[16][128]{int load_idx = threadIdx.x; // 0-511int row = load_idx / 32; // 0-15 (BN/4 = 128/4 = 32)int col = (load_idx % 32) * 4; // 0, 4, 8, ..., 124int globalRow = bk + row;int globalCol = blockColOffset + col;HALF4(s_b[row][col]) = HALF4(B[globalRow * N + globalCol]);}
Tensor Core 使用尝试 2:MMA(TBC)
事实上在了解完 WMMA 后才发现能直接用这个,打算日后再填坑。
小结
最后运行效率来说,对于 \(8192\times 8192\) 规模来说,直接分块是 145.2ms,tensor core 写法是 126.6ms。
两者不算严格的改进关系,更像是单独的两种写法。
使用 Nsight Compute 软件观察两个 Kernel 的计算情况(紫色为 Tensor core 写法,绿色是仅有分块):

这里说明 Tensor Core 写法的瓶颈不在计算(因为 Tensor Core 很快),而是等待内存加载;分块写法则是计算成为主要工作。
虽然后者利用率更高,但是总体而言前者使用了更合适的硬件,仍然能达到更快的水平(某些情况下,高利用率不等于高性能)。
Occupancy 方面:
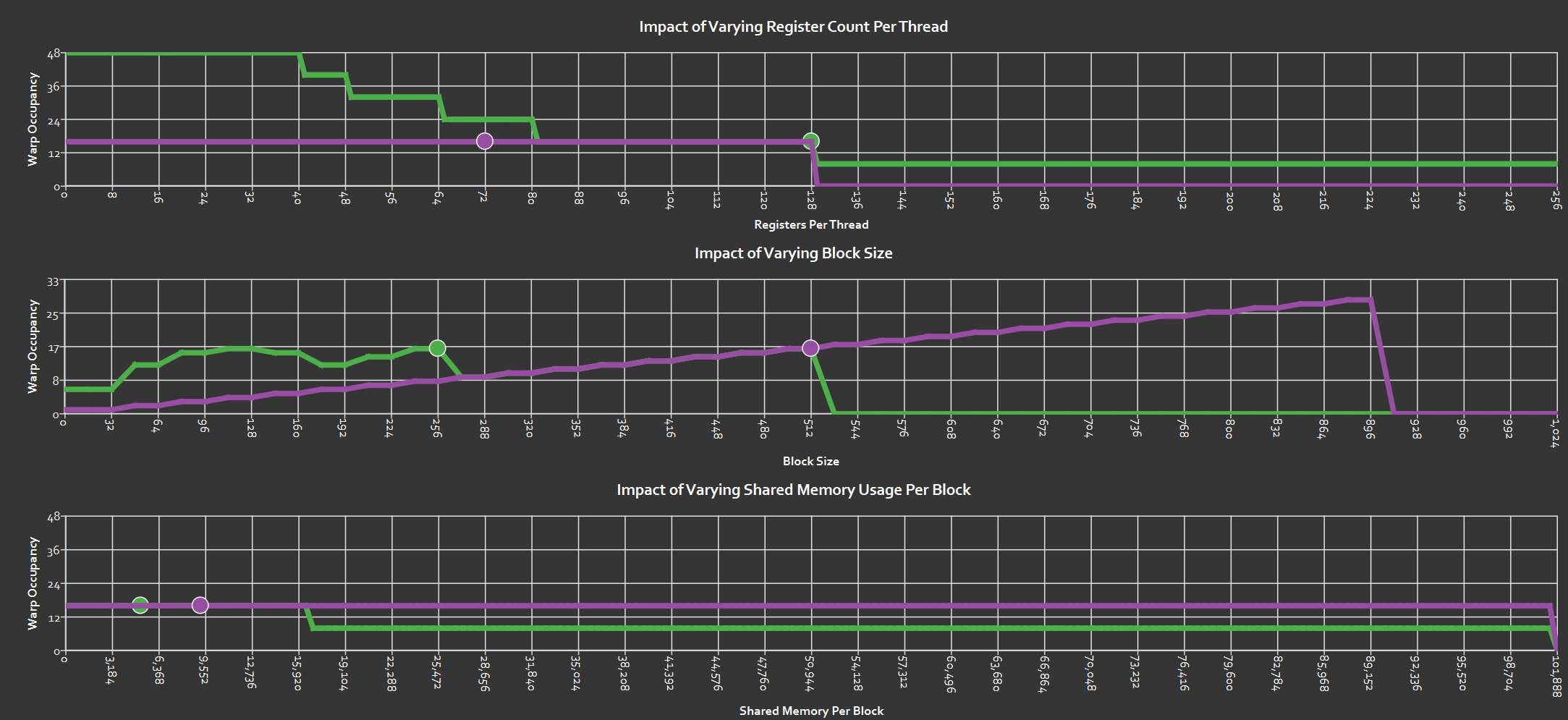
这图目前还不太会看,先挂在这里。
当然应该还有很多没有处理好的地方可以再做优化,目前就先写到这里。很多东西理解的不完全正确,当然学习存在一个过程,这些误解和忽视的细节会在实践的积累下被逐步解决。
