前言
总概
本文章将会向你讲解排列与组合的基本知识和综合运用。
会从定义、问题导入、解决方法、经典例题、总结等方面讲解。
前置知识
- 有一定的数学思维能力和理解能力
- 加法计数原理
- 乘法计数原理
- 阶乘
加法计数原理和乘法计数原理会在附录进行讲解。
排列
定义
排列的定义为:从给定的 $n$ 个不同元素中,取出指定个数为 $m(m \le n)$ 的元素进行排序。
排列的重点在于要进行排序,与元素顺序有关。
排列相当于是选择后再排序。
排列数的定义为从给定的 $n$ 个不同元素中,取出指定个数为 $m(m \le n)$ 的元素所有排列的个数。
我们用 $A_n^m$ 表示如上定义。
问题导入
现在有 $5$ 个元素,分别为 $a,b,c,d,e$。要求从这 $5$ 个元素中任取两个排成列的所有可能的个数。
我们之前可能通过暴力枚举来解决问题:
$(a,e)$ $(b,e)$ $(c,e)$ $(d,e)$ $(a,d)$ $(b,d)$ $(c,d)$ $(e,d)$ $(a,c)$ $(b,c)$ $(d,c)$ $(e,c)$ $(a,b)$ $(c,b)$ $(d,b)$ $(e,b)$ $(b,a)$ $(c,a)$ $(d,a)$ $(e,a)$ 其中 $(x,y)$ 表示排列所构成的二元组,可以发现,一共有 $20$ 种可能。
但是我们也可以通过乘法计数原理解决:
我们分 $2$ 次选择,第一次显然有 $5$ 种选法,第二次时,由于第一次选择了一个,所以第二次只有 $5 - 1 = 4$ 种选法了。
然后由乘法计数原理得出,一共有 $5 \times 4 = 20$ 种不同的选法。
这样子以来,我们就可以用 $A_5^2 = 20$ 来表示这个结果。
如果这道题变成要求从这 $5$ 个元素中任取三个排成列的所有可能的个数该怎么做呢?
我们还是可以通过暴力枚举,但是画图太麻烦了,但也可以得出一共有 $60$ 种,这种办法并不适用于数据大的排列。
然后再尝试通过乘法计数原理解决:
我们第一次可以选 $5$ 个,但是第二次选的时候只能选 $5 - 1 = 4$ 个,第三次选的时候只能选 $4 - 1 = 3$ 个,然后总共就有 $5 \times 4 \times 3 = 60$ 种。
我们用 $A_5^3 = 60$ 来表示上述结果。
排列的求法
对于 $A_n^m$ 来说,我们将它抽象成选元素,即从 $n$ 个元素种选 $m$ 个所有排列的个数。
我们第一次可以选 $n$ 个,第二次可以选 $n-1$ 个,第三次可以选 $n-2$ 个,以此类推。然后根据乘法计数原理就可以得出以下公式:
$$A_n^m=n(n-1)(n-2)\dots(n-m+1)$$
那么我们变换再化简一下,也就得到了:
$$A_n^m=\frac{n(n-1)(n-2)\dots(n-m+1)(n-m)\dots\times1}{(n-m)(n-m-1)\dots\times1}
\
=\frac{n!}{(n-m)!}
$$
我们就得出了求 $A_n^m$ 的公式。
组合
定义
组合的定义为:从给定的 $n$ 个不同元素中,取出指定个数为 $m(m \le n)$ 的元素不进行排序。
组合的重点在于要不进行排序,与元素顺序无关。
组合相当于是选择的结果。
组合数的定义为从给定的 $n$ 个不同元素中,取出指定个数为 $m(m \le n)$ 的元素所有组合的个数。
我们用 $C_n^m$ 表示如上定义。
问题导入
现在有 $5$ 个元素,分别为 $a,b,c,d,e$。要求从这 $5$ 个元素中任取两个组合的所有可能的个数。
注意到,刚才是排列,现在是组合,我们先把刚才的暴力枚举的表拿出来:
$(a,e)$ $(b,e)$ $(c,e)$ $(d,e)$ $(a,d)$ $(b,d)$ $(c,d)$ $(e,d)$ $(a,c)$ $(b,c)$ $(d,c)$ $(e,c)$ $(a,b)$ $(c,b)$ $(d,b)$ $(e,b)$ $(b,a)$ $(c,a)$ $(d,a)$ $(e,a)$ 可以发现,有些二元组对于组合来说是重复了的。
例如 $(a,b)$ 和 $(b,a)$ 就是相同的,也就是说,每一组数对于组合来说重复了 $2$ 次。
首先,我们用 $C_5^2$ 来表示上述的答案,那么怎么求呢?
我们刚才知道,每个数对于组合来说重复了 $2$ 次,所以我们就可以得到:
$$C_5^2 = \frac{A_5^2}{2} = 10$$
如果这道题变成要求从这 $5$ 个元素中任取三个组合的所有可能的个数该怎么做呢?
我们从上文知道,要求排列数,就是 $A_5^3 = 60$ 即可,但是如何求组合呢?
我们就要看每组数对于组合来说重复了几次,也就是求这个三元组可以组成多少种排列,即 $A_3^3$。
所以对于 $C_5^3$ 来说,答案就为:
$$C_5^3 = \frac{A_53}{A_33} = \frac{60}{6} = 10$$
组合的求法
我们首先了解全排列:
对于 $A_n^m$ 来说,若 $n = m$ 则这个排列数就是全排列。
要求组合数,最重要的就是知道对于组合来说重复的个数。
若取出 $m$ 个元素,那么重复的次数就是这 $m$ 个元素所组成的排列数,也就是 $A_m^m$。不难发现,重复的次数就是 $m$ 的全排列。
所以就可以得到以下公式:
$$ C_n^m = \frac{A_nm}{A_mm}$$
再将它展开和化简,就可以得到最后的公式了:
$$\begin{aligned}
C_n^m &= \frac{n(n-1)(n-2)\dots(n-m+1)}{m!}\
&= \frac{n!}{m!(n-m)!}
\end{aligned}
$$
这就是我们想要的公式了。
经典例题
做题之前
我们已经了解了排列与组合的基本知识,现在让我们来做一些题,巩固一下知识吧!
我们要了解在什么时候用排列,在什么时候用组合。
有序的安排我们使用排列;无序的选择我们使用组合。因为排列是有序的,而组合是无序的。
排列和组合的单独应用
从 $8$ 名学生中挑选 $1$ 人搬东西,挑选 $1$ 人帮老师接水,挑选 $1$ 人接送老师,共有几种不同方案?
看到挑选,也就是选择,我们使用组合。
挑选 $1$ 人搬东西,也就是从 $8$ 个人中选择 $1$ 个人,即 $C_8^1$ 为答案。
挑选 $1$ 人帮老师接水,也就是从 $7$ 个人中选择 $1$ 人,因为刚才选走了一个人,所以现在只有 $7$ 个。即 $C_7^1$ 为答案。
挑选 $1$ 人接送老师,也就是从 $6$ 个人中选择 $1$ 人,因为刚才选走了两个人,所以现在只有 $6$ 个。即 $C_6^1$ 为答案。
然后根据乘法计数原理计算最终答案:
$$ans = C_8^1 \times C_7^1 \times C_6^1 = 336$$
但是这一道题就不可以用排列吗?当然可以!
我们将题看成将 $8$ 名学生安排到 $3$ 个任务里面去,这不就是 $A_8^3$ 吗?
我们通过计算可以得出这和刚才的答案是一样的!
$$ans = A_8^3 = \frac{8!}{(8-3)!} = 336$$
排列与组合的综合应用
有 $3$ 个苹果和 $3$ 个香蕉,现在选择 $2$ 个苹果和 $2$ 个香蕉,每天吃一个水果,问有多少种安排方法。
我们一步一步看问题,看到先选择,就用组合。
从 $3$ 个苹果中选 $2$ 个,也就是 $C_3^2$;从 $3$ 个香蕉中选 $2$ 个,也是 $C_3^2$。
然后我们看见安排方法,就用排列。
我们将问题抽象为,将这 $4$ 个水果安排进 $4$ 天的位置里面,也就是 $A_4^4$。
最后就可以运用乘法计数原理求出答案:
$$ans = C_3^2 \times C_3^2 \times A_4^4 = 216$$
排列与组合的逆向思考
从 $3$ 名社恐和 $5$ 名社牛中挑选 $1$ 人搬东西,挑选 $1$ 人帮老师接水,挑选 $1$ 人接送老师,要求至少要有 $1$ 名社恐,共有几种不同方案?
这一题相比前面的题多了一个要求,考虑解决这个要求。
我们采用排列的思想,也就是将问题抽象成:将 $8$ 个人放进 $3$ 个任务里面,要求至少 $1$ 名社恐。
但是如何解决这个要求呢?我们正面思考的话,对于这个要求来说,可能会有 $1$ 个或 $2$ 个或 $3$ 个社恐,非常麻烦。所以我们考虑逆向思考。
要求至少有 $1$ 名社恐,逆向思考就是没有社恐呗,也就是全是社牛。也就是 $A_5^3$
而我们只用拿全部排列数减去全是社牛的排列数,不就是有社恐的排列数吗?
总共的排列数可以求出来,即 $A_8^3$ 为答案;而全是社牛的排列数已经求了出来,所以这题的答案就出来了:
$$ans = A_8^3 - A_5^3 = 276$$
排列与组合的特殊元素问题
-
位置问题
有 $6$ 个人甲、乙、丙、丁、戊、己排成一横排,最左方只能是甲或者是乙,且最右端不能是甲,问有多少种排列方法。
这一题除了要求排列方法,还有要求,并且甲的事最多,所以从甲入手。
由题可得,甲只能在 $1$ 号位至 $5$ 号位之间,但是当甲再 $1$ 号位的时候与再 $2$ 至 $5$ 号位时是不同的,所以对甲进行分类讨论。
当甲在 $1$ 号位时,就可以将问题抽象为将乙、丙、丁、戊、己放进后面的 $5$ 个位置,即 $A_5^5$ 为答案。
当甲不在 $1$ 号位时,即在 $2$ 至 $5$ 号位时,可以抽象为将甲安排进这 $4$ 个位置,即 $A_4^1$ 为答案。
因为甲不在 $1$ 号位上,所以乙就必须在 $1$ 号位上,这样才满足条件。
然后就是将丙、丁、戊、己放进剩余的 $4$ 个位置,也就是 $A_4^4$ 为答案。
最后的甲不在 $1$ 号位的总方案数就为 $A_4^1 \times A_4^4$。
那么最后只要将两种情况加起来就是总方案数了:
$$ans = A_5^5 + A_4^1 \times A_4^4 = 216$$
-
捆绑问题
有 $5$ 个人甲、乙、丙、丁、戊排成一横排,甲不能站在两端,丙要和丁相邻,问有多少种不同的排列方法。
这一题除了有位置要求之外,丙还要和丁相邻,我们可以先处理这个条件。
我们将丙和丁看成一个元素,再和甲、乙和戊排队,所以只剩下了 $4$ 个位置。
但是计算之前,我们发现丙和丁是可以交换位置的,因为丙和丁之间也要排队,所以事先要求出 $A_2^2$ 的值。
我们再来看另一个条件,也就是甲不能在两端,那么说明甲只能在 $2$ 号位或者 $3$ 号位,因为一共就 $4$ 个位置。那么甲要在这两个位置之中选择一个,也就是 $C_2^1$。
然后就只剩下了戊、丙丁和乙,也就是将这 $3$ 个元素(我们将丙丁看作了一个元素)安排进这 $3$ 个位置里面,即 $A_3^3$。
最后我们通过乘法计数原理求出答案即可:
$$ans = A_2^2 \times C_2^1 \times A_3^3 = 24$$
-
插空问题
有 $6$ 个人甲、乙、丙、丁、戊、己排成一横排,甲乙必须相邻,丙丁不能相邻,问有多少种不同的排列方法。
这一题除了有捆绑问题还有不相邻的要求,我们想考虑捆绑。
我们将甲和乙看作一个元素,那么就有 $A_2^2$ 种排列方法。
再和戊和己排队,也就是将 $3$ 个元素放进 $3$ 个位置里面,也就是 $A_3^3$ 种排列方式。
我们再来考虑不相邻的要求,我们假设甲乙、戊、己排队之后是下面的样子:
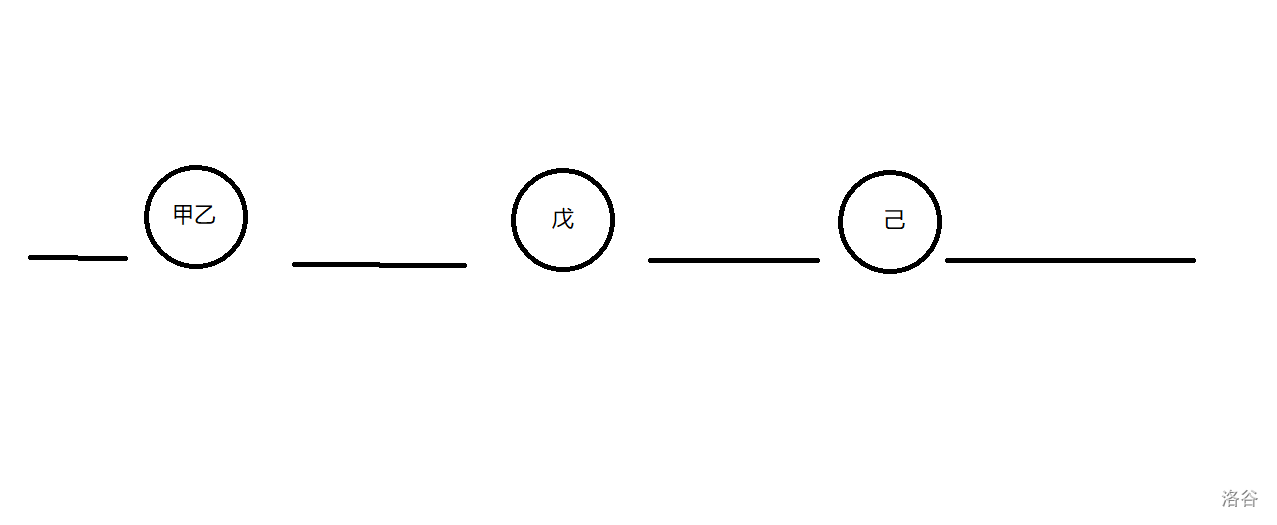
那么要使丙丁不相邻,那么他们两个就只能在画横线的空位上面,这样就不会相邻了。
这里共有 $4$ 个横线,也就是将两个人安排进 $4$ 个位置,即 $A_4^2$ 为答案。
最后运用乘法计数原理求出答案即可:
$$ans = A_2^2 \times A_3^3 \times A_4^2 = 144$$
排列与组合的排列数字问题
现有 $6$ 个数字从 $0$ 到 $5$,问这 $6$ 个数字能组成的不相同的四位偶数的个数。
看见这道题之后,发现这和前面的题都不一样,但是先别慌。
看见了四位偶数,可以得到 $2$ 个信息:
- 末尾数字只能是 $0$ 或 $2$ 或 $4$ 这三个
- 首位数字不能是 $0$ 这个数字
那么这道题不就变成了排队类型的问题吗?看见数字 $0$ 的事情最多,所以从 $0$ 入手。
我们类比上面的位置问题,分类讨论数字 $0$ 的位置在末尾和不在末尾的两种情况。
若数字 $0$ 在末尾的位置,那么现在就是将其余的 $5$ 个数字放进还剩的 $3$ 个位置里面,即 $A_5^3$。
若数字 $0$ 不在末尾的位置,也就是末尾是 $2$ 或 $4$ 的情况。那么我们就要将 $2$ 或 $4$ 安排进 $1$ 个位置里面,也就是 $A_2^1$ 了。
我们还注意到首位不能是 $0$ 这个数字,所以也就是将 $5-1=4$ 个数安排进 $1$ 个位置,即 $A_4^1$ 了。注意这 $4$ 个数中不含数字 $0$。
最后就只剩了 $2$ 个位置,也就是将剩下的 $4$ 个数放进 $2$ 个位置里面,即 $A_4^2$ 了。
然后运用乘法计数原理求出这种情况的答案,也就是 $A_2^1 \times A_4^1 \times A_4^2$ 这个值。
最后的答案就是将这两种情况加起来即可:
$$ans = A_5^3 + A_2^1 \times A_4^1 \times A_4^2 = 156$$
总结
排列与组合其实说简单也不简单,说难其实也难,所以多做题有助于提升对这类题型的敏感度,所以这里有一些课后思考题:
-
求方程 $x_1+x_2+x_3+x_4=8$ 的正整数解的个数
-
现有 $6$ 个数字从 $0$ 到 $5$,问这 $6$ 个数字能组成的不相同的五位奇数的个数
-
$5$ 名运动员分配 $3$ 个项目,每个运动员至少分配 $1$ 个项目,每个项目至少分配 $1$ 名运动员,求不同方案的种数。
