\(Tarjan\)
作用:
首先,我们要了解一个东西:强联通分量。
\(OI-Wiki\) 里说:
强连通的定义是:有向图 G 强连通是指,G 中任意两个结点连通。
强连通分量(Strongly Connected Components,SCC)的定义是:极大的强连通子图。
\(Tarjan\) 算法可以用来求强连通分量和缩点,同时,\(Tarjan\) 也可以用来求割点与桥及双联通分量,后文会讲。
求强连通分量:
前置:
首先,我们要了解一个东西,叫做 DFS 生成树。
虽然我感觉这个东西不了解也行
我们以图为例:
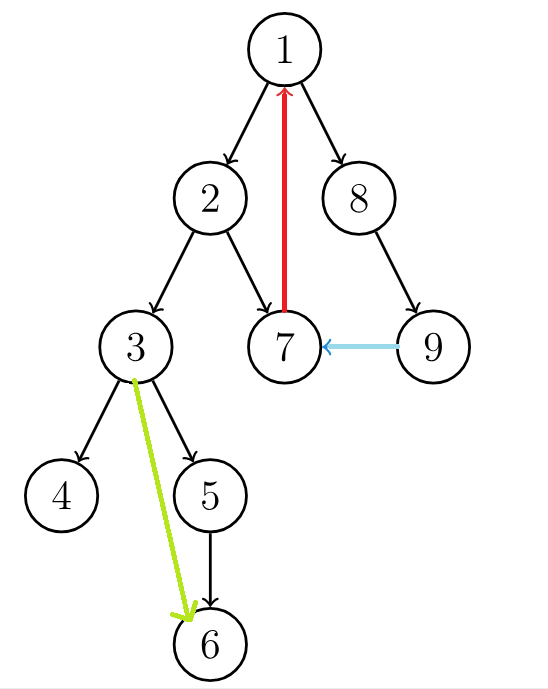
图中分为 \(4\) 种边,分别是:
- 树边,也就是图中黑色的边,它是我们 DFS 遍历到的边,它们构成了一个 DFS 树。
- 返祖边,也就是图中红色的边,它是一个点连向其祖先的边。
- 横叉边,也就是图中蓝色的边,它是连接两个不同子树的的边。
- 前向边,也就是图中绿色的边,它是在搜索子树的过程中形成的。
那 DFS 生成树有什么用呢?
如果我们搜索到的点,是某个强连通分量在搜索树中遇到的第一个结点,那该强联通分量的其余节点一定在他的子树中。
过程:
\(Tarjan\) 算法主要是基于 DFS 进行运行的。
同时 \(Tarjan\) 维护了一个栈,用来维护还没有进入强连通分量的点。
\(Tarjan\) 针对每个点 \(i\) 定义了一些东西:
- \(dfn_i\),表示在 DFS 中是第几个被搜到的。\((dfs\) 序\()\)
- \(low_i\),表示在当前点的子树中,能够直接到达的在栈中且 \(dfn\) 值最小的那个点的 \(dfn\) 值。
注意:在有向图和无向图中,\(low\) 的定义不同。
\(Tarjan\) 的大体过程是这样的:
-
初始化当前点的 \(dfn\) 和 \(low\) ,将当前点入栈,标记当前点已经入栈。
-
遍历当前点 \(now\) 所有能够到达的点 \(i\),同时:
- 如果 \(i\) 还未被遍历,那 \(i\) 就是 \(now\) 的儿子,遍历 \(i\),通时根据定义使 \(low_{now}=\min(low_{now},low_i)\)。
- 如果 \(i\) 已经被遍历过了且还在栈中,那说明 \(i\) 和 \(now\) 处于同一强连通分量,使 \(low_{now}=\min(low_{now},dfn_i)\)。
-
遍历完后,如果 \(dfn_{now}=low_{now}\) 那说明子树中的点都比他大,也就是子树中的点无法到达比 \(now\) 还小的点,那此时栈中的点就是一个强联通分量。清除栈中点的标记并对它们染色。
如果没有看懂,想要例子,可以来这里,讲的例子的确很详细。
代码:
int dfn[1000010],low[1000010],vis[1000010],color[1000010];
int idx,n,m,sccsum;
vector<int>mp[1000010];//这里作者使用vector存的图,链式前向星也可以。
stack<int>s;
void TJ(int now){//加入一个点dfn[now]=low[now]=++idx; //初始化dfn和lows.push(now); //入栈vis[now]=1; //标记当前点在栈里//搜索每个联通的点for(int i:mp[now]){ //本句等价于for(int i=0;i<mp[now].size();i++),然后下文的i变为mp[now][i]即可if(!dfn[i]){ //之前没访问过这个点TJ(i); //访问low[now]=min(low[now],low[i]); //其实这里也可以理解为让low[now]=当前强联通分量的"根"的dfn}else if(vis[i]){ //之前访问过,并且在栈里low[now]=min(low[now],dfn[i]); //说明访问到的点与现在这个点处于同一强联通分量}}//判断是否是根if(dfn[now]==low[now]){ //说明 现在这个点是根sccsum++; //强联通分量的数量+1int top; //栈顶元素do{top=s.top(); //取栈顶元素vis[top]=0; //vis归零s.pop(); //弹出color[top]=sccsum; //染色}while(now!=top);}
}
习题:
\(B3609\) [图论与代数结构 701] 强连通分量 - 洛谷
题意及思路:
单纯板子题,不过要求按顺序输出强连通分量,那我们直接存到 vector 里,然后排个序即可。
代码:
//#pragma GCC optimize("O2")
#include<bits/stdc++.h>
using namespace std;
int dfn[100010],low[100010],vis[100010],sccsum,idx;
vector<int> color[100010];
vector<int>mp[100010];
stack<int>s;
struct node{int id,fir;bool operator <(const node &W)const{return fir<W.fir;}
}a[100010];
void tarjan(int now){dfn[now]=low[now]=++idx;s.push(now);vis[now]=1;for(int i:mp[now]){if(!dfn[i]){tarjan(i);low[now]=min(low[now],low[i]);}else if(vis[i]){low[now]=min(low[now],dfn[i]);}}if(dfn[now]==low[now]){sccsum++;int top;do{top=s.top();s.pop();vis[top]=0;color[sccsum].push_back(top);}while(now!=top);}
}
int main(){int n,m;cin>>n>>m;for(int i=1;i<=m;i++){int l,r;cin>>l>>r;mp[l].push_back(r);}for(int i=1;i<=n;i++){if(!dfn[i]){tarjan(i);}}cout<<sccsum<<"\n";for(int i=1;i<=sccsum;i++){sort(color[i].begin(),color[i].end());a[i].id=i;a[i].fir=color[i][0];}sort(a+1,a+sccsum+1);for(int i=1;i<=sccsum;i++){for(int j:color[a[i].id]){cout<<j<<" ";}cout<<"\n";}return 0;
}
\(P2863\) [USACO06JAN] The Cow Prom S - 洛谷
题意及思路:
依旧模板题,要求输出大小大于一的强连通分量的个数,我们记一下每个强连通分量的大小即可。
代码:
//#pragma GCC optimize("O2")
#include<bits/stdc++.h>
using namespace std;
int dfn[100010],low[100010],vis[100010],sccsum,idx,ans;
vector<int> color[100010];
vector<int>mp[100010];
stack<int>s;
void tarjan(int now){dfn[now]=low[now]=++idx;s.push(now);vis[now]=1;for(int i:mp[now]){if(!dfn[i]){tarjan(i);low[now]=min(low[now],low[i]);}else if(vis[i]){low[now]=min(low[now],dfn[i]);}}if(dfn[now]==low[now]){sccsum++;int top;do{top=s.top();s.pop();vis[top]=0;color[sccsum].push_back(top);}while(now!=top);}
}
int main(){int n,m;cin>>n>>m;for(int i=1;i<=m;i++){int l,r;cin>>l>>r;mp[l].push_back(r);}for(int i=1;i<=n;i++){if(!dfn[i]){tarjan(i);}}for(int i=1;i<=sccsum;i++){if(color[i].size()>1){ans++;}}cout<<ans;return 0;
}
\(P1726\) 上白泽慧音 - 洛谷
题意及思路:
要求求出最大的强连通分量,我们用 vector 记一下即可。
代码:
//#pragma GCC optimize("O2")
#include<bits/stdc++.h>
using namespace std;
int dfn[100010],low[100010],vis[100010],sccsum,idx;
vector<int> color[100010];
vector<int>mp[100010];
stack<int>s;
struct node{int id,fir;bool operator <(const node &W)const{return fir>W.fir;}
}a[100010];
void tarjan(int now){dfn[now]=low[now]=++idx;s.push(now);vis[now]=1;for(int i:mp[now]){if(!dfn[i]){tarjan(i);low[now]=min(low[now],low[i]);}else if(vis[i]){low[now]=min(low[now],dfn[i]);}}if(dfn[now]==low[now]){sccsum++;int top;do{top=s.top();s.pop();vis[top]=0;color[sccsum].push_back(top);}while(now!=top);}
}
int main(){int n,m;cin>>n>>m;for(int i=1;i<=m;i++){int l,r,t;cin>>l>>r>>t;mp[l].push_back(r);if(t==2){mp[r].push_back(l);}}for(int i=1;i<=n;i++){if(!dfn[i]){tarjan(i);}}for(int i=1;i<=sccsum;i++){sort(color[i].begin(),color[i].end());a[i].id=i;a[i].fir=color[i].size();}sort(a+1,a+sccsum+1);cout<<color[a[1].id].size()<<"\n";for(int j:color[a[1].id]){cout<<j<<" ";}return 0;
}
缩点:
缩点其实就是将每个强联通分量看成一个点,然后被缩点后的图一定是一个 \(DAG\) (拓扑图)。
然后就可以进行一些操作了。
缩点后要重新建图,代码如下:
for(int i=1;i<=n;i++){mp[i].clear();
}
for(int i=1;i<=m;i++){//to存的是边if(color[to[i].l]!=color[to[i].r]){mp[color[to[i].l]].push_back(color[to[i].r]);}
}
习题:
\(P2341\) [USACO03FALL / HAOI2006] 受欢迎的牛 G - 洛谷
题意及思路:
要求在缩点后求出该图唯一一个出度为 \(0\) 的强连通分量,若有多个或没有,输出 \(0\)。
那我们在缩点后计算出度,遍历所有强连通分量,查看是否正好有一个出度为 \(0\) 的强连通分量,最后输出即可。
代码:
//#pragma GCC optimize("O2")
#include<bits/stdc++.h>
using namespace std;
int dfn[1000010],low[1000010],vis[1000010],color[1000010],outsum[1000010],siz[1000010];
int idx,n,m,sccsum;
vector<int>mp[1000010];
stack<int>s;
void TJ(int now){dfn[now]=low[now]=++idx;s.push(now);vis[now]=1;for(int i:mp[now]){if(!dfn[i]){TJ(i);low[now]=min(low[now],low[i]);}else if(vis[i]){low[now]=min(low[now],dfn[i]);}}if(dfn[now]==low[now]){sccsum++;int top;do{siz[sccsum]++;top=s.top();vis[top]=0;s.pop();color[top]=sccsum;}while(now!=top);}
}
int main(){cin>>n>>m;for(int i=1;i<=m;i++){int l,r;cin>>l>>r;mp[l].push_back(r);}for(int i=1;i<=n;i++){if(!dfn[i]){TJ(i);}}for(int i=1;i<=n;i++){for(int j:mp[i]){if(color[i]!=color[j]){outsum[color[i]]++;}}}int ans=0,sum=0;for(int i=1;i<=sccsum;i++){if(!outsum[i]){ans=siz[i];sum++;}}if(sum==1){cout<<ans;}else{cout<<0;}return 0;
}
