CF1032F Vasya and Maximum Matching
图论、树上问题、DP、Ad-hoc
考虑最大匹配唯一意味着什么,注意到树一定是一个二分图,树的最大匹配即二分图最大匹配,最大匹配唯一意味着没有增广环。
因为树上没有环,所以增广环一定含 \(S\) 或 \(T\),形如:
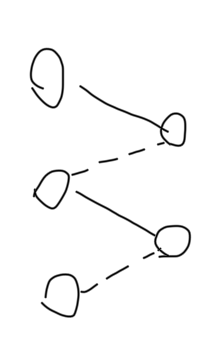
或
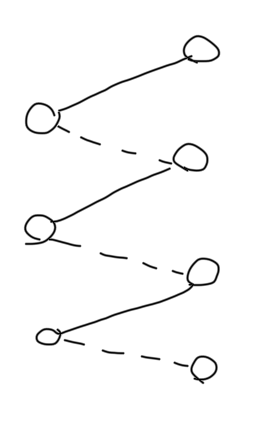
注意到如果存在长度 \(>3\) 的增广环,一定可以缩减为长度 \(=3\) 的增广环。形式化地,最大匹配唯一当且仅当对于一个最大匹配,不存在 \(u,v,w\in V\),使得 \((u,v)\) 为匹配边,\((v,w)\) 为非匹配边,且 \(w\) 没有匹配。
似乎还是不太能做,考虑 \(w\) 没有匹配意味着什么,发现只要有一个点有边相连却没有匹配就已经爆了,于是发现关键结论:树的最大匹配唯一当且仅当存在完美匹配。
证明:
先证必要性,最大匹配唯一 \(\Rightarrow\) 存在完美匹配:
若不存在完美匹配,则必然有一个点 \(u\) 失配,考虑其相邻一点 \(v\)。若 \(v\) 有匹配,则出现增广环,最大匹配不唯一;否则可将 \((u,v)\) 改为匹配边,原匹配不是最大匹配。
再证充分性,存在完美匹配 \(\Rightarrow\) 最大匹配唯一:
将当前匹配看成一个最大流,则 \(S\) 没有出度,\(T\) 没有入度,二分图内部无环,因此不可能存在增广环。
证毕。
于是考虑 DP,设 \(f_{u,0/1/2}\) 表示 \(u\) 的子树中,\(u\) 没有保留的边 / \(u\) 没有匹配 / \(u\) 有匹配。
初始状态:
\[f_{u,0}=1
\]
转移:
\[\begin{cases}
f_{u,0} &\leftarrow f_{u,0}(f_{v,0}+f_{v,2}) \\
f_{u,1} &\leftarrow f_{u,0}f_{v,2}+f_{u,1}(f_{v,0}+2f_{v,2}) \\
f_{u,2} &\leftarrow (f_{u,0}+f_{u,1})(f_{v,0}+f_{v,1})+f_{u,2}(f_{v,0}+2f_{v,2})
\end{cases}
\]
答案:
\[f_{rt,0}+f_{rt,2}
\]
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
typedef pair<int,ll> pil;
typedef pair<ll,int> pli;
typedef pair<ll,ll> pll;
template<typename T>
void chkmin(T &x,const T &y){x=min(x,y);}
template<typename T>
void chkmax(T &x,const T &y){x=max(x,y);}
const int inf=0x3f3f3f3f;
const ll infll=0x3f3f3f3f3f3f3f3f;
const int MOD=998244353;
const int N=300005;
int n;
ll f[N][3];
vector<int> G[N];
void dfs(int u,int fa){f[u][0]=1;for(auto v:G[u]){if(v==fa) continue;dfs(v,u);f[u][2]=((ll)(f[u][0]+f[u][1])*(f[v][0]+f[v][1])%MOD+(ll)f[u][2]*(f[v][0]+f[v][2]*2)%MOD)%MOD;f[u][1]=((ll)f[u][0]*f[v][2]%MOD+(ll)f[u][1]*(f[v][0]+f[v][2]*2)%MOD)%MOD;f[u][0]=(ll)f[u][0]*(f[v][0]+f[v][2])%MOD;}
}
int main(){scanf("%d",&n);for(int i=1;i<n;i++){int u,v;scanf("%d%d",&u,&v);G[u].push_back(v),G[v].push_back(u);}dfs(1,1);printf("%lld\n",(f[1][0]+f[1][2])%MOD);return 0;
}
