1. 论文介绍
论文题目:Learning Discrete Structures for Graph Neural Networks
论文领域:图神经网络,图结构学习
论文地址: https://arxiv.org/abs/1903.11960
论文发表:ICML 2019
论文代码:https://github.com/lucfra/LDS-GNN.
论文背景:

2. 论文摘要
图神经网络(GNNs)是一类流行的机器学习模型,其主要优点是能够在数据点之间加入稀疏和离散的依赖结构。不幸的是,GNNs只能在这种图结构可用时使用。然而,在实践中,现实世界中的图形通常是嘈杂的和不完整的,或者根本不可用。在这项工作中,我们提出了联合学习图卷积网络(GCN)的结构和参数的近似求解一个双层程序,学习离散概率分布在图的边缘。这不仅允许在给定图形不完整或损坏的场景中应用GCN,而且允许在图形不可用的场景中应用GCN。我们进行了一系列的实验,分析了所提出的方法的行为,并证明它优于相关的方法的一个显著幅度。
3. 相关介绍
3.1 图神经网络
双层隐GCN的表达式可以表达为
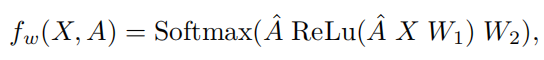
最小化带有正则化项目和经验损失函数
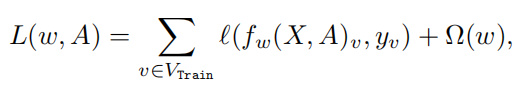
对于GCN的双层优化问题为
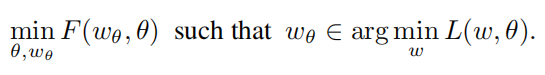
3.2 结构与参数的联合学习
通过采用期望值,内部和外部目标都成为伯努利参数的连续(并且可能是平滑)函数。方程给出的双水平问题。
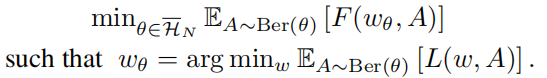
4. 论文核心算法LDS
整个算法的框架可以分为两层,目的是学习数据点之间的离散和稀疏依赖关系,同时训练图卷积网络GCN的参数。
LDS的整体架构图为
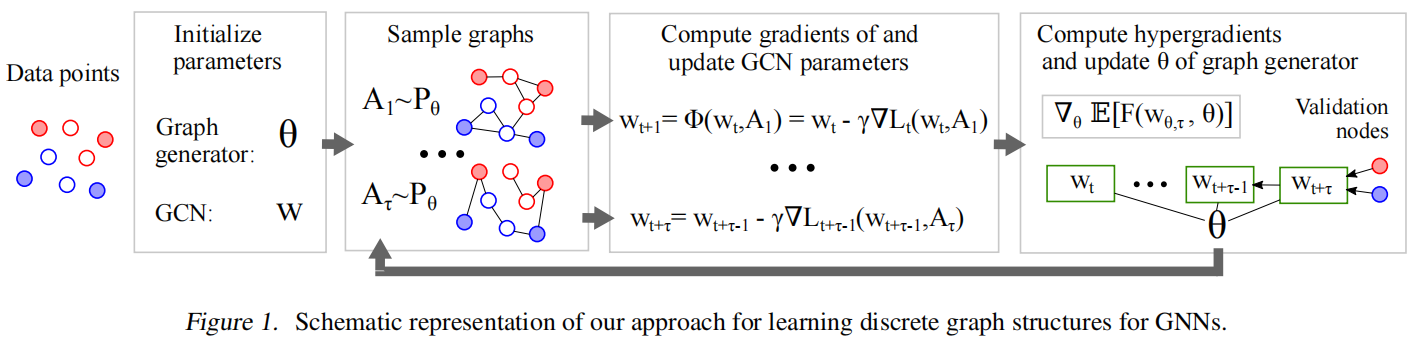
LDS算法的核心逻辑:
- 协同优化:内层目标函数和外层目标函数交替进行优化
- 离散可解:通过Gumbel-Softmax重参数化,将离散图结构的优化转化为连续概率的优化,解决传统离散组合优化“NP-hard”的求解难题。
算法的步骤可以分为三个步骤
- 第一步,对于非图数据,根据KNN近邻算法建立图结构数据。针对输入数据节点,利用图生成器生成图(一般是以KNN为基础的算法)
- 第二步,进行图采样,来优化内层目标函数(该内层目标函数是GCN的权重参数),在这个过程中,固定外层的图邻接矩阵这个参数
- 第三步,在完成内层目标函数优化之后,再进行优化外层目标函数,固定GCN的权重参数,继续优化图邻接矩阵。
LDS算法的伪代码图

5. 实验设置
实验评价的三个标准:
(1)评估了 LDS 的节点分类问题,其中图结构可用,但缺少一定比例的边。
(2)验证我们的假设,即LDS 可以在没有图表的半监督分类问题上取得竞争性结果。
(3)分析了学习到的图生成模型,以了解 LDS 即使在大部分边缺失的情况下也能在多大程度上学习有意义的边概率分布。
实验数据为UCI非图结构数据和图数据Cora,Citeseer。
对比算法:
LDS 与普通 GCN 进行了比较。此外,构思了一种方法(GCN-RND),在普通 GCN 的每个优化步骤中添加随机采样的边缘。
实验数据表现对比
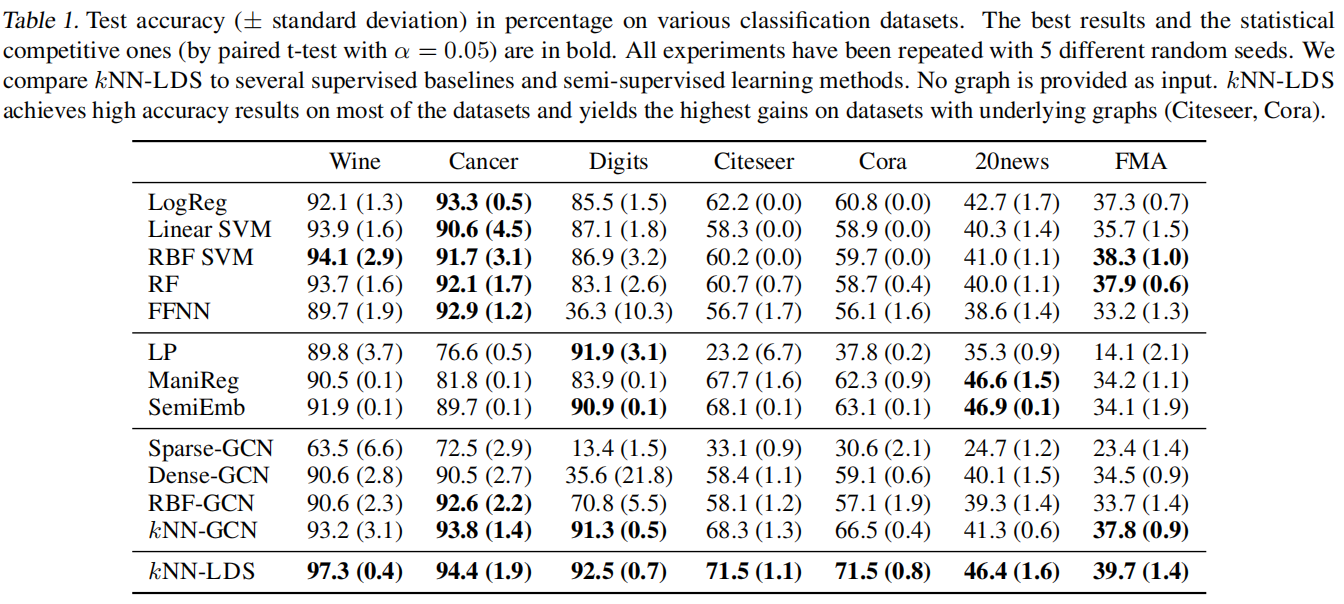
不同算法在Cora 和 Citeseer数据集上的表现。
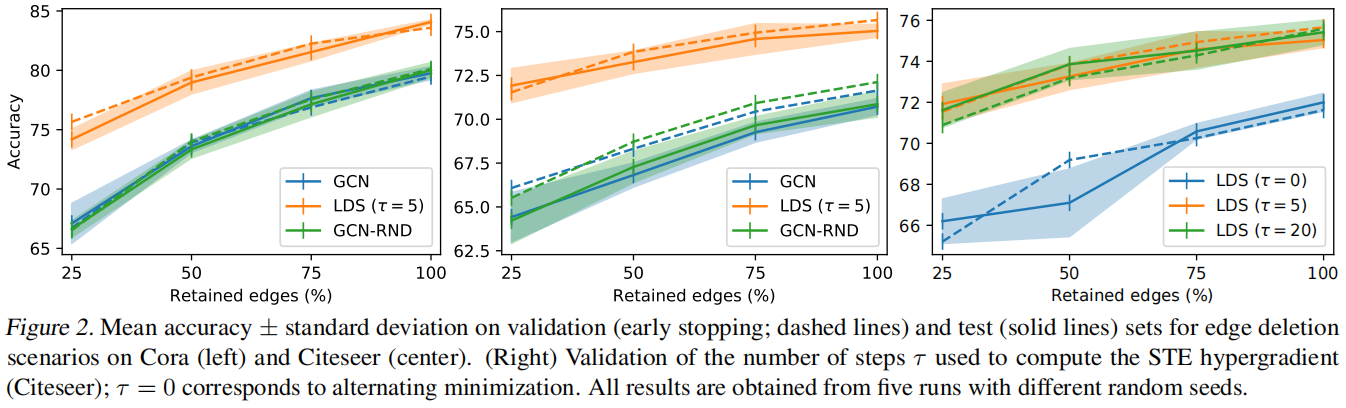
在分类层之前的输出,不同的算法对Citeseer数据集的类划分和可视化过程。

6. 总结
图结构学习领域的经典论文。在非图结构数据中,通过建立样本的节点间连接来辅助
LDS 的优势在于它以合理的计算成本在典型的半监督分类数据集上获得了高精度。此外,由于 LDS 学习的图生成模型,边缘参数具有概率解释。
7. 个人感悟
学习如何构造一个用来GNN操作的图数据,同样也优化了整个数据分类的表现。图数据在数据分类的鲁棒性上会有良好的增强效果。
