复矩阵的奇异值分解(SVD)
定理
设 $ A \in \mathbb{C}_r^{m \times n} $,则存在 $ U \in \mathcal{U}_m $($ m $ 阶酉矩阵)和 $ V \in \mathcal{U}_n $($ n $ 阶酉矩阵),使得
$$
U^\dagger A V = \begin{pmatrix} \Sigma_r & 0 \\ 0 & 0 \end{pmatrix}
$$
其中 $ \Sigma_r = \text{diag}(\sigma_1, \dots, \sigma_r) $($ r $ 阶对角矩阵),且 $ \sigma_1 \geq \dots \geq \sigma_r > 0 $($ \sigma_i $ 为 $ A $ 的非零奇异值)。
证明
由于 $ A^\dagger A $ 是半正定的 Hermite 矩阵(对任意向量 $ x $,$ x^\dagger (A^\dagger A) x = (A x)^\dagger (A x) \geq 0 $,且 $ (A^\dagger A)^\dagger = A^\dagger A $),且 $ \text{rank}(A^\dagger A) = \text{rank}(A) = r $,根据「Hermite 矩阵的谱定理」,存在 $ n $ 阶酉矩阵 $ V = [v_1, \dots, v_n] \in \mathcal{U}_n $,使得:
$$
V^\dagger (A^\dagger A) V = \mathrm{diag}(\sigma_1^2, \dots, \sigma_n^2)
$$
其中 $ \sigma_1 \geq \dots \geq \sigma_r > 0 $,$ \sigma_{r+1} = \dots = \sigma_n = 0 $($ \sigma_i^2 $ 为 $ A^\dagger A $ 的特征值)。
令 $ V_1 = [v_1, \dots, v_r] $($ V $ 中对应非零奇异值的前 $ r $ 列),$ V_2 = [v_{r+1}, \dots, v_n] $($ V $ 中对应零奇异值的后 $ n-r $ 列),$ \Sigma_r = \text{diag}(\sigma_1, \dots, \sigma_r) $,则有:
$$
V_1^\dagger (A^\dagger A) V_1 = \Sigma_r^2
$$
$$
V_2^\dagger (A^\dagger A) V_2 = 0
$$
- 第一个等式表明 $ (A V_1)^\dagger (A V_1) = \Sigma_r^2 $,即 $ A V_1 $ 的列向量两两正交(内积为 0),且第 $ i $ 列的模长为 $ \sigma_i $;
- 第二个等式表明 $ (A V_2)^\dagger (A V_2) = 0 $,即 $ A V_2 $ 的所有列向量均为零向量($ A V_2 = 0 $)。
因此,令
$$
U_1 = A V_1 \Sigma_r^{-1}
$$
则 $ U_1^\dagger U_1 = (\Sigma_r^{-1})^\dagger (A V_1)^\dagger (A V_1) \Sigma_r^{-1} = \Sigma_r^{-1} \Sigma_r^2 \Sigma_r^{-1} = I_r $,即 $ U_1 $ 的列向量是 $ \mathbb{C}^m $ 中的标准正交向量组。
再取 $ U_2 \in \mathbb{C}^{m \times (m - r)} $(将 $ U_1 $ 的列向量扩展为 $ \mathbb{C}^m $ 的标准正交基,满足 $ U_2^\dagger U_1 = 0 $),令 $ U = [U_1, U_2] \in \mathcal{U}_m $($ m $ 阶酉矩阵),则:
$$
U^\dagger A V = \begin{pmatrix} U_1^\dagger A V_1 & U_1^\dagger A V_2 \\ U_2^\dagger A V_1 & U_2^\dagger A V_2 \end{pmatrix}
$$
分别计算分块矩阵的每个元素:
- $ U_1^\dagger A V_1 = U_1^\dagger (U_1 \Sigma_r) = \Sigma_r $(因 $ A V_1 = U_1 \Sigma_r $);
- $ U_1^\dagger A V_2 = U_1^\dagger \cdot 0 = 0 $(因 $ A V_2 = 0 $);
- $ U_2^\dagger A V_1 = U_2^\dagger (U_1 \Sigma_r) = 0 $(因 $ U_2^\dagger U_1 = 0 $);
- $ U_2^\dagger A V_2 = U_2^\dagger \cdot 0 = 0 $(因 $ A V_2 = 0 $)。
因此:
$$
U^\dagger A V = \begin{pmatrix} \Sigma_r & 0 \\ 0 & 0 \end{pmatrix}
$$
几何意义
对于SVD分解
$$A = U \begin{pmatrix} \Sigma_r & 0 \\ 0 & 0 \end{pmatrix} V^\dagger$$
可以进一步写成**截断的SVD分解**:
$$A = \tilde{U} \Sigma_r \tilde{V}^\dagger$$
其中:
- $\tilde{U} \in \mathrm{St}(m,r)$($m \times r$ 矩阵,列向量为标准正交基,属于Stiefel流形),即 $U$ 中对应非零奇异值的前 $r$ 列;
- $\tilde{V} \in \mathrm{St}(n,r)$($n \times r$ 矩阵,列向量为标准正交基),即 $V$ 中对应非零奇异值的前 $r$ 列。
于是$Ax$相当于先对$x$做一个$\mathbb{C}^n\to \mathbb{C}^r$的保范映射,再在$\mathbb{C}^r$中做一个缩放变换$(\Sigma_r)$, 最后再做一个$\mathbb{C}^r\to \mathbb{C}^m$的保范映射.
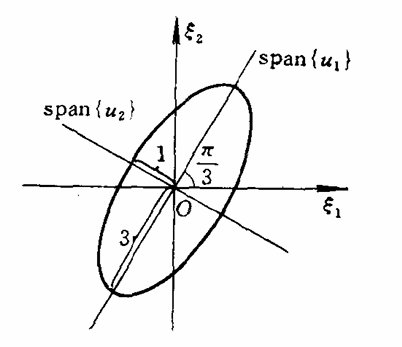
考虑一个简单的例子(出自徐树方的书)。设
$$
A = [u_1, u_2] \begin{bmatrix} 3 & 0 \\ 0 & 1 \end{bmatrix} [v_1, v_2]^T,
$$
其中 $ u_1 = \left( \frac{1}{2}, \frac{\sqrt{3}}{2} \right)^T $, $ u_2 = \left( \frac{\sqrt{3}}{2}, -\frac{1}{2} \right)^T $, $ v_1 = \left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)^T $, $ v_2 = \left( \frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2} \right)^T $。那么对任意的 $ x = \xi_1 v_1 + \xi_2 v_2 \in \mathbb{R}^2 $,有
$$
y = Ax = \eta_1 u_1 + \eta_2 u_2,
$$
其中 $ \eta_1 = 3\xi_1 $,$ \eta_2 = \xi_2 $。因此,如果 $ \| x \|_2 = 1 $,即 $ \xi_1^2 + \xi_2^2 = 1 $,则对应的 $ y = \eta_1 u_1 + \eta_2 u_2 $ 满足
$$
\frac{\eta_1^2}{3^2} + \eta_2^2 = 1.
$$
这表明 $ A $ 将 $ \mathbb{R}^2 $ 中的单位圆 $ \{ x \in \mathbb{R}^2: \| x \|_2 = 1 \} $ 变成了椭圆 $ E_2 = \{ y = Ax: \| x \|_2 = 1 \} $,而两个奇异值正好是这一椭圆的两个半轴长;长轴所在的直线是 $ \text{span}${$u_1$} ,短轴所在的直线是 $ \text{span}${$u_2$ } ,它们分别是 $ \text{span}${$ v_1 $} $ 和span {$v_2$} 的像(如下图所示)。