【转载出处:知乎】 尊重原版权,如有侵权请告知,将立即删除
在定积分的章节中,反常积分刚开始学总是让人苦恼的,笔者在刚接触这一块的时候纠结于,反常积分,定积分,广义积分,这些都是个啥?而在反常积分的学习中,有一个非常重要的考点——敛散性的判别。只有收敛的反常积分我们才可以求其值。本篇文章为大家提供一个判别敛散性的方法:极限审敛法。
在进入正题之前,我们先回顾一些基础的概念:
正常积分(定积分):曲线下的面积是定值。
反常积分(广义积分):曲线下的面积是某个趋势。趋于定值,则收敛;趋于无穷,则发散。
反常积分可以分为三类:
1. 区间无界。 如[1,+∞)
2. 区间有界,函数无界。 (瑕积分)
3. 区间无界且函数无界
同样的,对不同种类的反常积分极限审敛法有所不同,下面进入正文:
区间无界的极限审敛法:

该法则需要注意的有两点:1.区间无界 2.限制因子p>1。
可笑的是,2024年数学二的选择压轴题竟然考察了这个最简单的定义!
该法则直观的解释,即:若要判断一个区间无界的反常积分是否收敛,我们用一个x的高次阶去乘以这个函数,判断这个组合体在x->∞的时候极限是否存在,若存在,则收敛;反之发散。
对于做题,大家只要记住这个法则怎么使用就可以了,这已足够。
下面我们来看两个例子:


通过这两个例子请读者体会极限审敛法在无穷区间的反常积分中的应用。
下面为读者提供一道好题供练习:

下面是证明过程:

但是请注意,如下命题各位读者要注意:
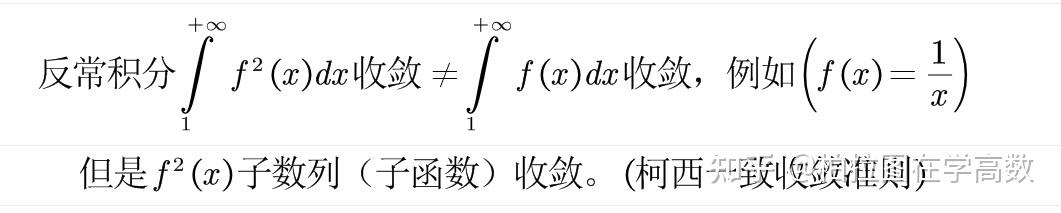
实际上,更为困难的是函数无界的反常积分,即瑕积分。
瑕积分的极限审敛法(重点中的重点!)
对于左瑕点:
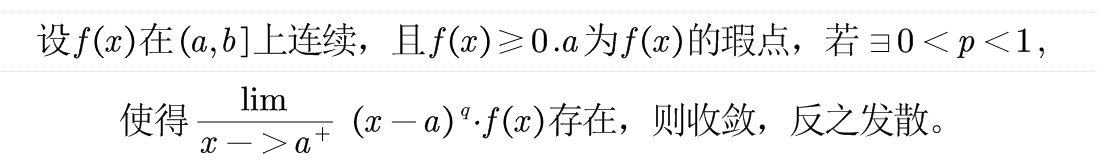
对于右瑕点:
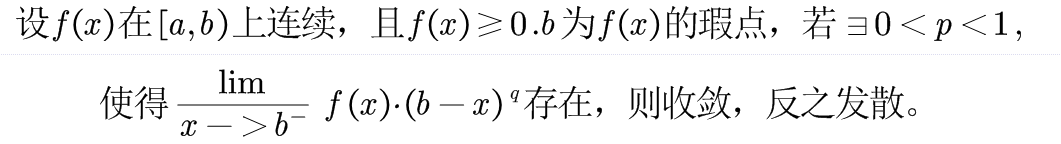
注意,在瑕积分中,限制因子p应当小于1!另外十分重要的是,当积分区间两端都为瑕点时,需要分开讨论,如:
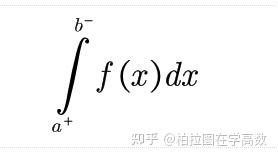
a,b分别为函数的左右两个端点(瑕点),此时需要将被积函数拆成(a,K]以及[K,b),分别讨论两个反常积分的敛散性,只有当他们都收敛时,原来的反常积分才收敛!!!
下面是一个例子:

这一点笔者在初学时也忽视了,这是非常重要的。另外请读者注意,定积分中的相关结论并不能推广到反常积分,这点在日后笔者会为大家做整理。
实际上,使用极限审敛法已经足够解决很多敛散性判定问题,但是在某些问题上,使用比较审敛法会更有奇效,同样这点在日后笔者会为大家做整理。
