3. 模型
使用前述的公式和参数化方法,我们现在来具体说明 OpenPBR 表面模型的结构。我们首先描述“非薄壁”情况(“薄壁”情况下的结构有所不同),其材质结构非正式地如下图所示:
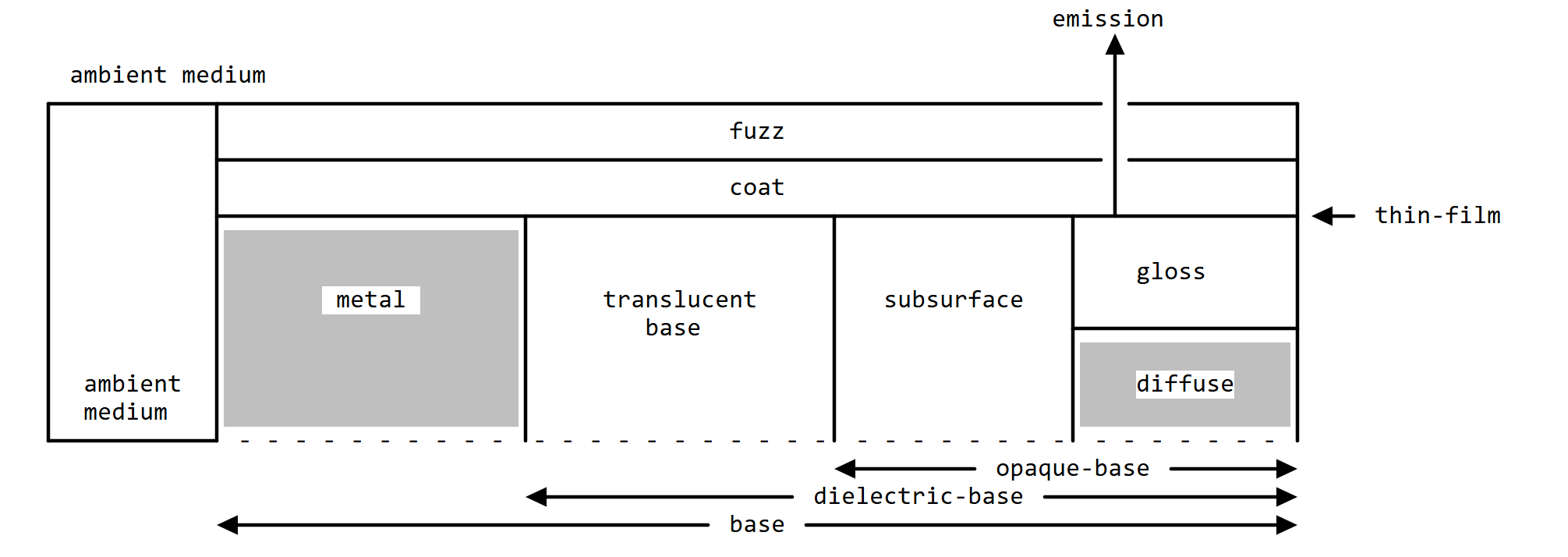
总而言之,其公式结构由以下层构成:

这些层通过以下方式组合成材质结构(下文记为 $ M_{\text{PBR}} $):
$$
M_{\text{PBR}} = \textbf{mix}(S_{\text{ambient-medium}}, M_{\text{surface}}, \alpha)\quad\text{where}\,\alpha = \text{geometry opacity}
$$
$$
M_{\text{surface}} = \textbf{layer}(M_{\text{coated-base}}, S_{\text{fuzz}}, F)\quad\text{where}\,F = \text{fuzz weight}
$$
$$
M_{\text{coated-base}} = \textbf{layer}(M_{\text{base-substrate}}, S_{\text{coat}}, C)\quad\text{where}\,C = \text{coat weight}
$$
$$
M_{\text{base-substrate}} = \textbf{mix}(M_{\text{dielectric-base}}, S_{\text{metal}}, M)\quad\text{where}\,M = \text{base metalness}
$$
$$
M_{\text{dielectric-base}} = \textbf{mix}(M_{\text{opaque-base}}, S_{\text{translucent-base}}, T)\quad\text{where}\,T = \text{transmission weight}
$$
$$
M_{\text{opaque-base}} = \textbf{mix}(M_{\text{glossy-diffuse}}, S_{\text{subsurface}}, S)\quad\text{where}\,S = \text{subsurface weight}
$$
$$
M_{\text{glossy-diffuse}} = \textbf{layer}(S_{\text{diffuse}}, S_{\text{gloss}})
$$
其结构呈现为由 layer 和 mix 操作生成的树形形式:
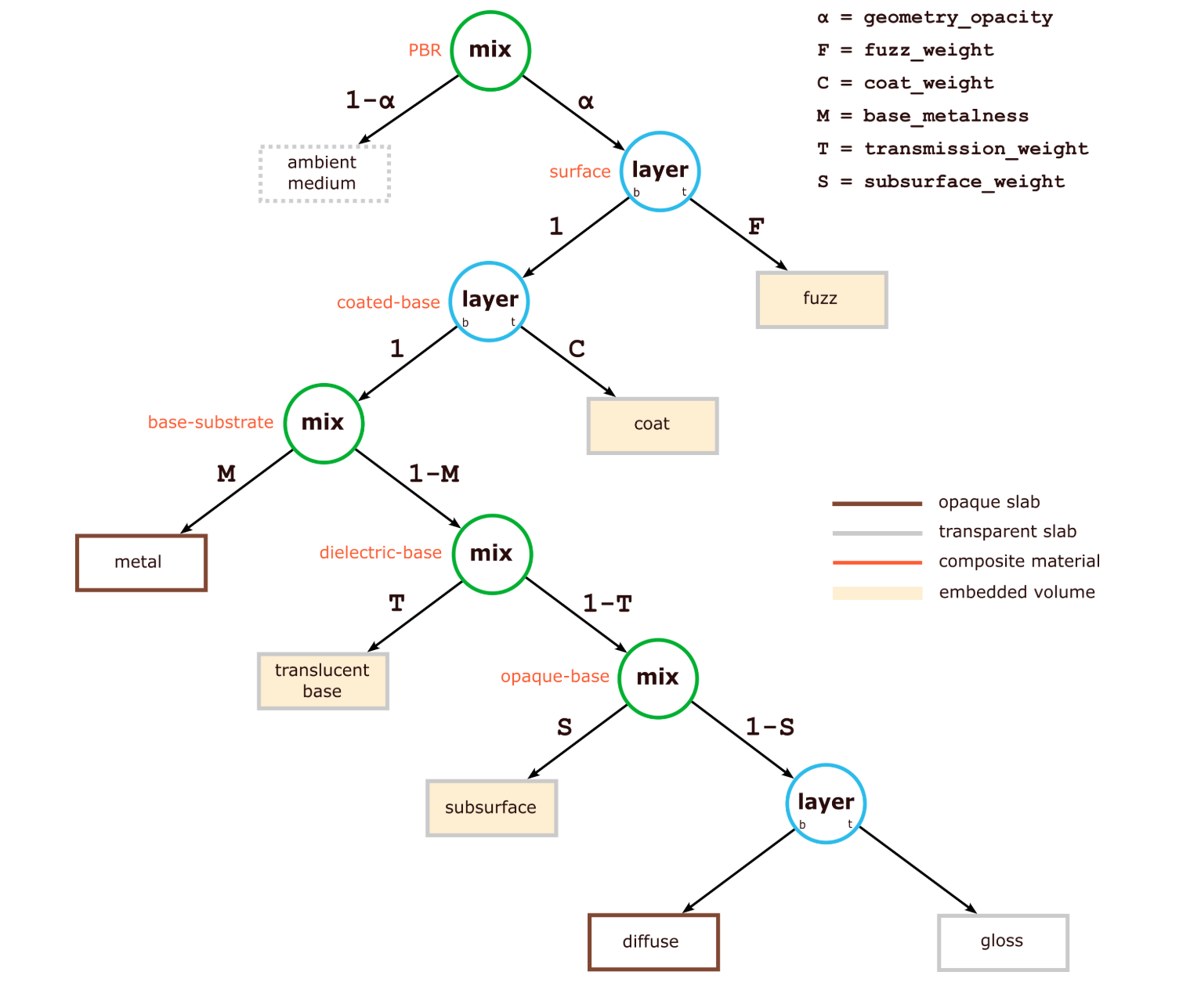
除了上述模型结构中明确列出的权重(weight)和不透明度(opacity)参数外,每个组件层(slab)的属性还由下文详述的更多参数控制(完整参数集请参阅“参数参考”部分)。
代码分析如下:
a. 首先保存光照方向、相机方向、法向方向、片元相机空间坐标、遮蔽系数等参数
b. 然后调用mx_sheen_bsdf函数,输入fuzz_weight、fuzz_color, fuzz_roughness, geometry_normal,输出fuzz_bsdf_out
BSDF fuzz_bsdf_out = BSDF(vec3(0.0),vec3(1.0));
mx_sheen_bsdf(closureData, fuzz_weight, fuzz_color, fuzz_roughness, geometry_normal, 1, fuzz_bsdf_out);
c. 然后调用mx_dielectric_bsdf函数,输入weight, tint, ior, roughness, thinfilm_thickness, thinfilm_ior, N, X, distribution, scatter_mode,输出coat_bsdf_out
BSDF coat_bsdf_out = BSDF(vec3(0.0),vec3(1.0));
mx_dielectric_bsdf(closureData, coat_weight, vec3(1.000000, 1.000000, 1.000000), coat_ior, coat_roughness_vector_out, 0.000000, 1.500000, geometry_coat_normal, geometry_coat_tangent, 0, 0, coat_bsdf_out);
d. 然后调用mx_generalized_schlick_bsdf函数,输入weight, color0, color82, color90, exponent, roughness, thinfilm_thickness, thinfilm_ior, N, X, distribution, scatter_mode,输出metal_bsdf_out
BSDF metal_bsdf_out = BSDF(vec3(0.0),vec3(1.0));
mx_generalized_schlick_bsdf(closureData, specular_weight_tf_inv_out, metal_reflectivity_out, metal_edgecolor_out, vec3(1.000000, 1.000000, 1.000000), 5.000000, main_roughness_out, 0.000000, 1.500000, geometry_normal, geometry_tangent, 0, 0, metal_bsdf_out);
e. 然后调用mx_generalized_schlick_bsdf函数,输入weight, color0, color82, color90, exponent, roughness, thinfilm_thickness, thinfilm_ior, N, X, distribution, scatter_mode,输出metal_bsdf_tf_out
再使用mx_add_bsdf将metal_bsdf_out, metal_bsdf_tf_out加起来得到metal_bsdf_tf_blend_out
BSDF metal_bsdf_tf_out = BSDF(vec3(0.0),vec3(1.0));
mx_generalized_schlick_bsdf(closureData, specular_weight_tf_out, metal_reflectivity_out, metal_edgecolor_out, vec3(1.000000, 1.000000, 1.000000), 5.000000, main_roughness_out, thin_film_thickness_nm_out, thin_film_ior, geometry_normal, geometry_tangent, 0, 0, metal_bsdf_tf_out);
BSDF metal_bsdf_tf_blend_out = BSDF(vec3(0.0),vec3(1.0));
mx_add_bsdf(closureData, metal_bsdf_out, metal_bsdf_tf_out, metal_bsdf_tf_blend_out);
f. 然后调用mx_dielectric_bsdf函数,输入weight, tint, ior, roughness, thinfilm_thickness, thinfilm_ior, N, X, distribution, scatter_mode,输出dielectric_reflection_out
BSDF dielectric_reflection_out = BSDF(vec3(0.0),vec3(1.0));
mx_dielectric_bsdf(closureData, thin_film_weight_inv_out, specular_color, modulated_eta_s_out, main_roughness_out, 0.000000, 1.500000, geometry_normal, geometry_tangent, 0, 0, dielectric_reflection_out);
调用mx_dielectric_bsdf函数,输入weight, tint, ior, roughness, thinfilm_thickness, thinfilm_ior, N, X, distribution, scatter_mode,输出dielectric_reflection_tf_out。同样使用mx_add_bsdf函数得到dielectric_reflection_blend_out
BSDF dielectric_reflection_tf_out = BSDF(vec3(0.0),vec3(1.0));
mx_dielectric_bsdf(closureData, thin_film_weight, specular_color, modulated_eta_s_out, main_roughness_out, thin_film_thickness_nm_out, thin_film_ior, geometry_normal, geometry_tangent, 0, 0, dielectric_reflection_tf_out);
BSDF dielectric_reflection_blend_out = BSDF(vec3(0.0),vec3(1.0));
mx_add_bsdf(closureData, dielectric_reflection_out, dielectric_reflection_tf_out, dielectric_reflection_blend_out);
g. 调用mx_dielectric_bsdf函数,输入weight, tint, ior, roughness, thinfilm_thickness, thinfilm_ior, N, X, distribution, scatter_mode,输出dielectric_transmission_out
BSDF dielectric_transmission_out = BSDF(vec3(0.0),vec3(1.0));
mx_dielectric_bsdf(closureData, 1.000000, if_transmission_tint_out, modulated_eta_s_out, main_roughness_out, 0.000000, 1.500000, geometry_normal, geometry_tangent, 0, 1, dielectric_transmission_out);
调用mx_anisotropic_vdf函数,输入absorption, scattering, anisotropy,输出dielectric_volume_out。再调用mx_layer_vdf函数混合dielectric_transmission_out, dielectric_volume_out得到dielectric_volume_transmission_out
BSDF dielectric_volume_out = BSDF(vec3(0.0),vec3(1.0));
mx_anisotropic_vdf(closureData, if_volume_absorption_out, if_volume_scattering_out, transmission_scatter_anisotropy, dielectric_volume_out);
BSDF dielectric_volume_transmission_out = BSDF(vec3(0.0),vec3(1.0));
mx_layer_vdf(closureData, dielectric_transmission_out, dielectric_volume_out, dielectric_volume_transmission_out);
h. 然后调用mx_oren_nayar_diffuse_bsdf函数,输入weight, color, roughness, N, energy_compensation,输出subsurface_thin_walled_reflection_bsdf_out,乘上系数得到subsurface_thin_walled_reflection_out
BSDF subsurface_thin_walled_reflection_bsdf_out = BSDF(vec3(0.0),vec3(1.0));
mx_oren_nayar_diffuse_bsdf(closureData, 1.000000, subsurface_color_nonnegative_out, base_diffuse_roughness, geometry_normal, false, subsurface_thin_walled_reflection_bsdf_out);
BSDF subsurface_thin_walled_reflection_out = BSDF(vec3(0.0),vec3(1.0));
mx_multiply_bsdf_color3(closureData, subsurface_thin_walled_reflection_bsdf_out, subsurface_thin_walled_brdf_factor_out, subsurface_thin_walled_reflection_out);
i. 然后调用mx_translucent_bsdf函数,输入weight, color, N,输出subsurface_thin_walled_transmission_bsdf_out,乘上系数得到subsurface_thin_walled_transmission_out。使用mx_mix_bsdf函数混合上一步值得到subsurface_thin_walled_out
BSDF subsurface_thin_walled_transmission_bsdf_out = BSDF(vec3(0.0),vec3(1.0));
mx_translucent_bsdf(closureData, 1.000000, subsurface_color_nonnegative_out, geometry_normal, subsurface_thin_walled_transmission_bsdf_out);
BSDF subsurface_thin_walled_transmission_out = BSDF(vec3(0.0),vec3(1.0));
mx_multiply_bsdf_color3(closureData, subsurface_thin_walled_transmission_bsdf_out, subsurface_thin_walled_btdf_factor_out, subsurface_thin_walled_transmission_out);
BSDF subsurface_thin_walled_out = BSDF(vec3(0.0),vec3(1.0));
mx_mix_bsdf(closureData, subsurface_thin_walled_reflection_out, subsurface_thin_walled_transmission_out, 0.500000, subsurface_thin_walled_out);
j. 然后调用mx_subsurface_bsdf函数,输入weight, color, radius, anisotropy, N,输出subsurface_bsdf_out。再使用mx_mix_bsdf函数混合subsurface_thin_walled_out, subsurface_bsdf_out得到selected_subsurface_out
BSDF subsurface_bsdf_out = BSDF(vec3(0.0),vec3(1.0));
mx_subsurface_bsdf(closureData, 1.000000, subsurface_color_nonnegative_out, subsurface_radius_scaled_out, subsurface_scatter_anisotropy, geometry_normal, subsurface_bsdf_out);
BSDF selected_subsurface_out = BSDF(vec3(0.0),vec3(1.0));
mx_mix_bsdf(closureData, subsurface_thin_walled_out, subsurface_bsdf_out, subsurface_selector_out, selected_subsurface_out);
k. 然后调用mx_oren_nayar_diffuse_bsdf函数,输入weight, color, roughness, N, energy_compensation,输出diffuse_bsdf_out。再混合selected_subsurface_out得到opaque_base_out。再混合dielectric_volume_transmission_out得到dielectric_substrate_out。再调用mx_layer_bsdf函数得到dielectric_base_out。
BSDF diffuse_bsdf_out = BSDF(vec3(0.0),vec3(1.0));
mx_oren_nayar_diffuse_bsdf(closureData, base_weight, base_color_nonnegative_out, base_diffuse_roughness, geometry_normal, true, diffuse_bsdf_out);
BSDF opaque_base_out = BSDF(vec3(0.0),vec3(1.0));
mx_mix_bsdf(closureData, selected_subsurface_out, diffuse_bsdf_out, subsurface_weight, opaque_base_out);
BSDF dielectric_substrate_out = BSDF(vec3(0.0),vec3(1.0));
mx_mix_bsdf(closureData, dielectric_volume_transmission_out, opaque_base_out, transmission_weight, dielectric_substrate_out);
BSDF dielectric_base_out = BSDF(vec3(0.0),vec3(1.0));
mx_layer_bsdf(closureData, dielectric_reflection_blend_out, dielectric_substrate_out, dielectric_base_out);
m. 最后混合metal_bsdf_tf_blend_out和dielectric_base_out得到base_substrate_out。乘以darkened_base_substrate_out得到darkened_base_substrate_out。乘以coat_attenuation_out得到coat_substrate_attenuated_out。调用mx_layer_bsdf函数得到coat_layer_out。调用mx_layer_bsdf函数得到fuzz_layer_out
// Calculate the BSDF response for this light source
BSDF base_substrate_out = BSDF(vec3(0.0),vec3(1.0));
mx_mix_bsdf(closureData, metal_bsdf_tf_blend_out, dielectric_base_out, base_metalness, base_substrate_out);
BSDF darkened_base_substrate_out = BSDF(vec3(0.0),vec3(1.0));
mx_multiply_bsdf_color3(closureData, base_substrate_out, modulated_base_darkening_out, darkened_base_substrate_out);
BSDF coat_substrate_attenuated_out = BSDF(vec3(0.0),vec3(1.0));
mx_multiply_bsdf_color3(closureData, darkened_base_substrate_out, coat_attenuation_out, coat_substrate_attenuated_out);
BSDF coat_layer_out = BSDF(vec3(0.0),vec3(1.0));
mx_layer_bsdf(closureData, coat_bsdf_out, coat_substrate_attenuated_out, coat_layer_out);
BSDF fuzz_layer_out = BSDF(vec3(0.0),vec3(1.0));
mx_layer_bsdf(closureData, fuzz_bsdf_out, coat_layer_out, fuzz_layer_out);
由于该模型本质上只是对材质结构的物理描述,因此原则上它适用于通过精确方法求解,例如[Jakob2014]、[Belcour2018]和[Zeltner2018]中开发的方法。这些方法试图计算光在整个层堆栈中所有不同的反射和透射模式,最终生成一个未必是各界面BSDF简单线性组合的最终BSDF。然而,我们希望此材质模型能够在广泛的渲染平台上使用,从离线路径追踪器一直到移动设备上的实时游戏引擎。强制规定特定的实现方式会使该材质模型在某些类别的渲染器中不实用,并最终降低模型的实用性。因此,我们将最终BSDF的具体实现方式的选择视为本规范范围之外的事项。
为了方便和效率,目前该模型最有可能被映射到一个由多种BSDF波瓣(lobe)混合组成的模型,类似于Autodesk Standard Surface着色器[Georgiev2019]及其在MaterialX中的表示。下文“简化为波瓣混合模型”部分将提供一个此类模型的推导示例。我们还基于此推导提供了一个MaterialX的参考实现。
接下来,我们将讨论此结构中各层的BSDF和介质的具体形式。
3.1 微平面模型
此处我们针对上一节所述模型中描述界面的各 BSDF 的形式和参数化给出一些通用假设。
金属、电介质、涂层和光泽漫反射板层的 BSDF,即 $ f_{\text{conductor}} $, $ f_{\text{dielectric}} $, $ f_{\text{coat}} $ 和 $ f_{\text{diffuse}} $,均假定由标准微平面模型描述。这是一种广泛使用的近似方法 [Pharr2023],其假设表面由光滑的金属、电介质或朗伯材质的微平面构成的高度场组成,这些面元的法线(称为微法线)的统计分布决定了宏观尺度的表面粗糙度特性。(绒毛模型则不同,它基于体积"微薄片"模型 [Heitz2015])。
在单次散射近似下,微平面 BRDF 具有如下标准形式⁴ [Walter2007], [Pharr2023]:
其中 $ h=(\omega_{i}+\omega_{o})/|\omega_{i}+\omega_{o}| $ 是半角向量,即能将 $ \omega_{i} $ 镜面反射至 $ \omega_{o} $ 的微法线。对于电介质,还存在 BTDF(即 BSDF 中输入和输出方向分别位于相对半球而非同一半球的部分),其形式与 BRDF 相似,但具有修正的半角向量和菲涅尔因子 [Walter2007]。
菲涅尔因子 $ F(\omega_{i},h) $ 由每个微平面的反射材料的复折射率(IOR)决定(更专业地说,由其与外部 IOR 的比值决定),其形式因材料是电介质还是导体而异 [Walter2007]。每种情况下的参数化将在"电介质基底"章节和"金属"章节中描述。
遮蔽阴影函数 $ G(\omega_{i},\omega_{o}) $ 解释了输入和输出方向被微平面遮挡的概率。它通常使用给定 NDF 后计算 $ G $ 的 Smith 模型推导得出,对于 GGX NDF(公式 18),其遮蔽阴影函数有一个众所周知的形式 [Heitz2014]。
法线分布函数(NDF)$ D(m) $ 描述了表面上微法线 $ m $ 出现的相对概率,从而决定了粗糙度特性。一种能很好近似真实材料粗糙度且广为流行的 NDF 是所谓的 GGX 分布(此名称源于"毛玻璃",但该公式最初由 Trowbridge 和 Reitz 提出 [Walter2007], [Burley2012], [Heitz2014], [Pharr2023]),其基本形式⁵ 为:
其中 $ \theta_{m} $ 是 $ m $ 与(宏观)表面法线之间的夹角,参数 $ \alpha $ 控制微平面的表观粗糙度。当 $ \alpha\to 0 $ 时,法线分布高度集中于 $ \theta_{m}=0 $ 附近,因此微平面大多平坦,呈现光滑外观;而当 $ \alpha $ 增大时,微平面变得越来越粗糙,呈现粗糙外观。实际上,我们将 $ \alpha $ 限制在范围 $ [0,1] $ 内,因为 $ \alpha>1 $ 不会产生 plausible 的粗糙外观。遵循 [Burley2012],我们设定(在各向同性情况下):
其中 $ r\in[0,1] $ 是面向用户的粗糙度参数,因为这样能在改变 r 时,使表观粗糙度的变化在感知上更线性。
在一般情况下,粗糙度是各向异性的,即法线分布函数(NDF)并非呈圆对称,而是沿着表面平面内的某个方向拉伸,导致高光沿该方向拉长。这模拟了由划痕或刷磨等工艺产生的连贯微观沟槽几何结构。我们假设已定义了一个参考切向量场(通过 geometry_tangent 和 geometry_coat_tangent 定义)。该参考切向量指示了 NDF 被拉伸的方向,意味着微观沟槽倾向于与副法线方向正交。
随后,各向异性情况下的 GGX 分布通过沿切向量和副法线方向的两个独立的粗糙度参数 $ \alpha_t $ 和 $ \alpha_b $ 进行参数化,具体形式如下(给定微法线 $ m $ 相对于切向量的极角 $ \phi_m $(以法线为轴逆时针测量)):
当 $ \alpha_t=\alpha_b=\alpha $ 时,此公式简化为各向同性形式。文献 [Heitz2018] 和 [Dupuy2023] 中提出了对采用各向异性 GGX 微平面模型的 BSDF 进行高效采样的技术。NDF 参数 $ \alpha_t $ 和 $ \alpha_b $ 可以更方便地参数化为总粗糙度 $ r $ 和各向异性程度 $ a\in[0,1] $。我们建议使用以下从 $ r \(、\) a $ 到 $ \alpha_t \(、\) \alpha_b $ 的映射关系:
该公式满足 \(\alpha_t^2+\alpha_b^2=2\alpha^2\),以保持平均粗糙度不随各向异性程度变化。其原理是,如果渲染器不支持各向异性(或者出于性能考虑,例如细节级别控制,而关闭了该功能),仅使用粗糙度参数应能产生一个在感知上与原始各向异性高光相近的各向同性高光。图 2 显示了所生成高光的形状(从技术上讲,这些是 NDF $ D_{\mathrm{GGX}}(m) $ 在二维斜率空间中的等高线)。
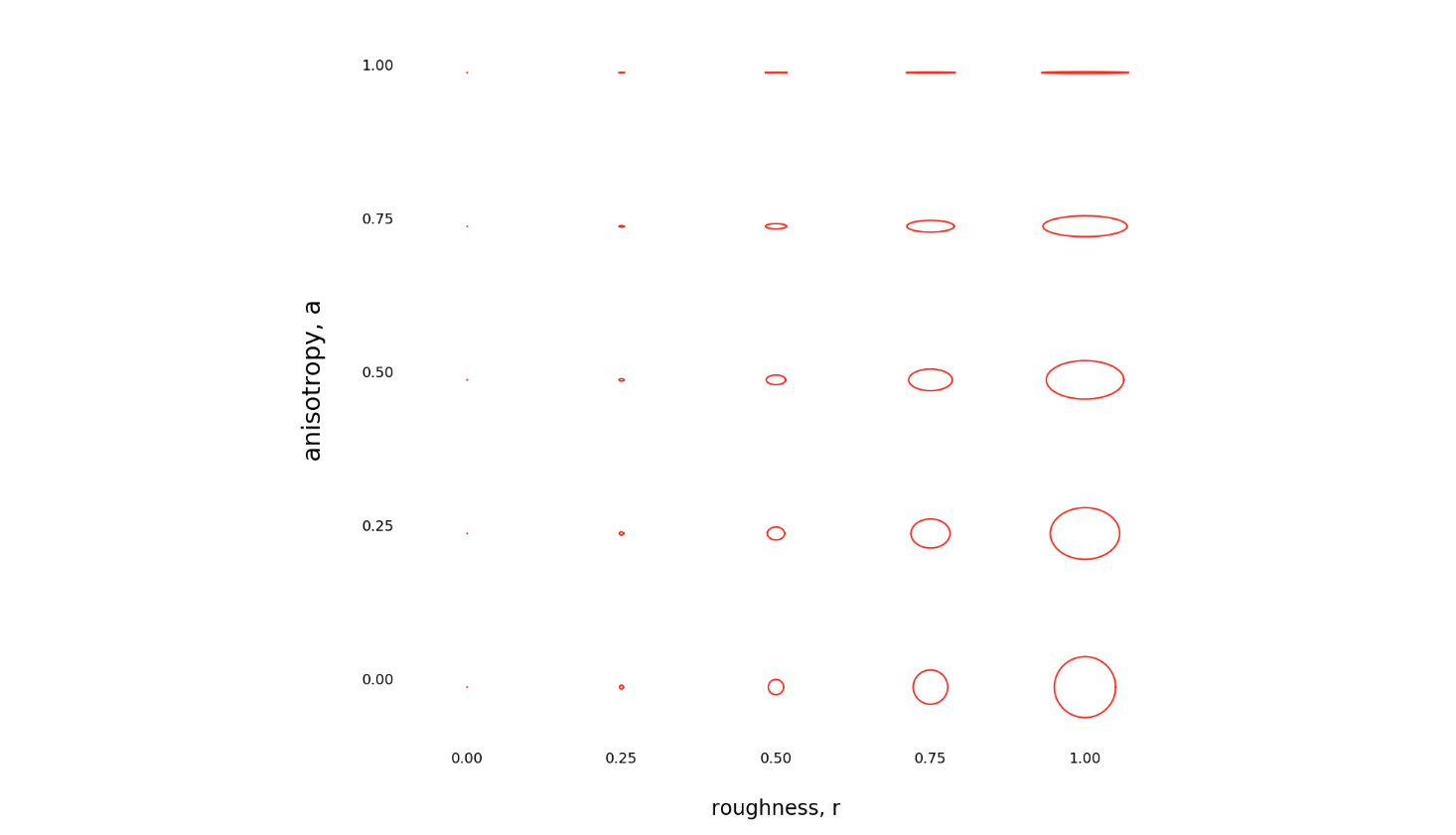
图 2:NDF形状随粗糙度r和各向异性程度a的变化关系
总结NDF参数化设定如下:电介质基底BSDF $ f_{\text{dielectric}} $ 和金属基底BRDF $ f_{\text{conductor}} $ 共享相同的参数,而涂层BSDF $ f_{\text{coat}} $ 使用独立的一组参数:
- specular_roughness(用于 $ f_{\text{dielectric}} $ 和 $ f_{\text{conductor}} $)与 coat_roughness(用于 $ f_{\text{coat}} $)定义了粗糙度参数 r。这些粗糙度被限制在 [0, 1] 范围内,因为 r = 1 对应感知上非常粗糙的表面。
- specular_roughness_anisotropy(用于 $ f_{\text{dielectric}} $ 和 $ f_{\text{conductor}} $)与 coat_roughness_anisotropy(用于 $ f_{\text{coat}} $)指定了 a ∈ [0, 1](即NDF沿局部表面切向方向拉伸的程度)。然后,根据公式 (21) 确定最终的NDF参数 $ \alpha_{t} $ 和 $ \alpha_{b} $。
需要注意的是,对于方向相反的切向量,高光的视觉效果是相同的;这也有利于在与其他支持方向各向异性的模型之间进行转换时保持数值的有效性。
公式 (17) 所描述的单次散射微面BRDF不满足能量守恒,因为它忽略了微面之间的多次散射。理想的实现方案应通过某种方法来解决此问题,否则粗糙金属和电介质的反射会显得比应有的更暗且饱和度更低。目前已有多种方案:
* [Heitz2016a] 中描述了一种完全精确的方法,通过蒙特卡洛方法显式模拟多次反射。
* [Kulla2017] 提出了更简化的近似模型,通过添加补偿波瓣来解释损失的能量。
* [Turquin2019] 提出了另一种近似模型,通过缩放波瓣的反照率来维持能量守恒,但牺牲了互易性。
