难题被逐层拆解,每一次的拆解都使它变得更为简单。分而治之揭示了一个重要的事实:从简单做起,一切都不再复杂。
1.1 分治算法
分治 是一种非常常见的算法策略。
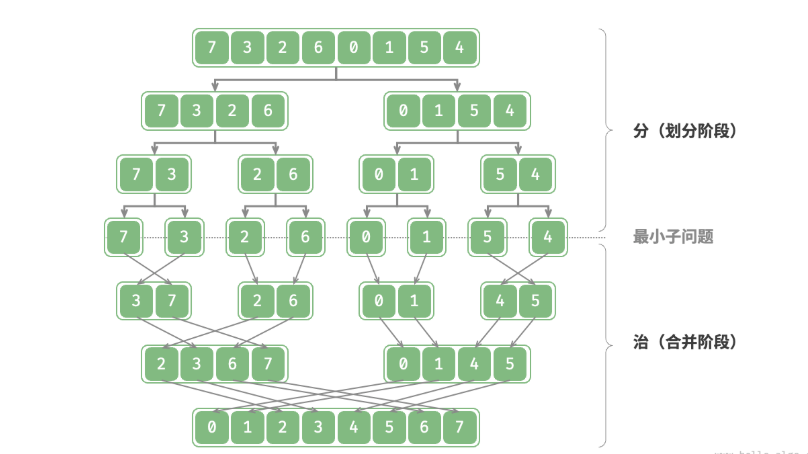
分:将整个问题划分为多个小问题。
治:从小问题开始,自底至顶将子问题合并成原来的问题。
1.2 分治的效率
分治往往可以提高效率。
- 降低时间复杂度
冒泡排序为例,处理长度为n的数组需要O(n^2),但是将其划分为两个小数组就只要O(n +(n/2)^2 +(n/2)^2 + n ) - 并行操作
子问题之间是相互独立的,利于并行操作。、
1.3 分治之二分搜索
- 题目描述
给定一个包含 n 个元素有序的(升序)整型数组 nums 和一个目标值 target,要求实现搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。题目保证nums中的所有元素都不重复。
#include<iostream>
using namespace std;
int find(int num[],int tar,int n){int l=0,r=n-1;while(l<=r){int mid=(l+r)/2;if(num[mid]==tar) return mid;else if(num[mid]<tar) l=mid+1;else r=mid-1;}return -1;
}
int main(){int n;cin>>n;int num[n];for(int i=0;i<n;i++){cin>>num[i];}int tar; cin>>tar;cout<<find(num,tar,n);return 0;
}
