本文章的核心思想来自labuladong的算法笔记网站,加上了我一些自己的学习心得,只用于学习用途。文章中的图片和代码都是原创,非转载。
背景
本人本科审计学,硕士软件工程,目前研究方向是ai在数据库领域的应用(目前还在啃ai,因为事情比较多,所以真的是边学边忘),高中开始接触了C语言,到大学编程算是一点小爱好,毕业后直接找了软件开发的工作(会计一点没学懂🐶)。家里不支持我做这行,他们觉得这行太牛马伤身体,我觉得都是划水,干什么不一样,和爱好沾边一点至少不会被折磨,后面工作了一段时间感觉这行相对来说蛮有意思,就有了跨专业的想法。
因为本科非科班,所以算法一直是我的软肋,考研的时候考的是408,408难度主要是内容比较多,以记忆和理解为主,特别是数据结构,基本是考一些原理和计算题,算法题就一道,一般能写出暴力解法也能拿一些分,所以我当时果断放弃了算法题,去啃其他的题,最后408成绩还算不错。but,不管是考研复试还是工作面试,算法的阴影一直挥散不去,所以,在今年开题报告通过后果断开始啃一下算法。教程的话我是看了labuladong的算法笔记。
以下笔记完全是个人对客观理论的主观理解,不是特别专业的技术文章,有不足之处求各位大佬鞭策(别抽脸哈)。
因为我最近刷算法用的是golang,再加上我比较懒,所以这里我就先使用golang编写了,后面有时间了我会换成c或者python(先用着,后面有时间再版本迭代)。
递归
“递归”这个名词我就不做解释了,如果不知道建议直接打开命令行输入“shutdown -h now”,简单的说递归就是“套娃”,就是那种娃娃玩偶,大的娃娃里面有一个小的,小的娃娃里面还有一个更小的,更小的娃娃里面还...直到再放不下更小的娃娃为止(也就是base case)。
举个最经典的例子——斐波那契数列
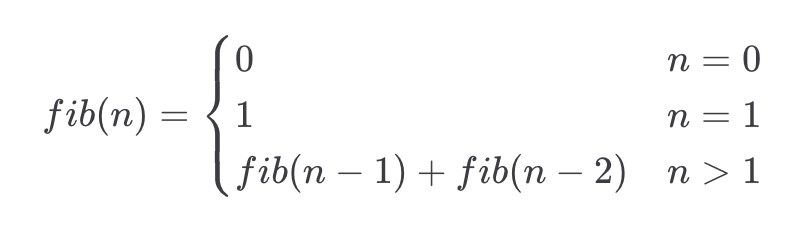
求解的算法代码如下:
func fib(n int) int {if n < 2 {return n}return fib(n - 1) + fib(n - 2)
}
假如我们求n=4的斐波那契数列,则调用fib(4),则fib(4)就是最外层的娃娃,fib(3)和fib(2)就是较小的娃娃,而fib(1)和fib(0)则是最小的娃娃,也就是base case,到这里递归结束,然后按相反的路线一层一层返回最外层。
二叉树
看这块内容前,我放东哥的两句至理名言:
- 算法的本质是穷举,递归是一种重要的穷举手段,递归的正确理解方法是从「树」的角度理解。
- 编写递归算法,有两种思维模式:一种是通过「遍历」一遍树得到答案,另一种是通过「分解问题」得到答案。
这两句话一定要深深的刻在脑海里。
“二叉”两个字在我们山东话里都和“傻”沾边,也就是我们山东人说的“潮巴”。其实二叉树并不傻,但学习它的人容易“潮巴”了。简单点说,二叉树就是一棵每个节点的子节点数不超过2的树。
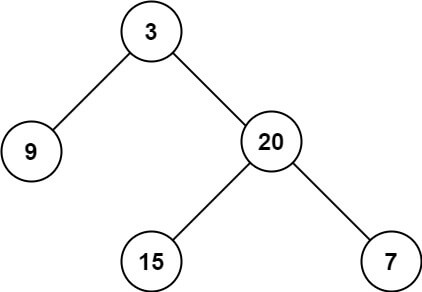
emmm...这么一看好像二叉树和递归并不沾边。别急,先让我们来看一下二叉树的遍历。二叉树一共有三种遍历方式:前序遍历、中序遍历和后序遍历。每种遍历方式有递归和迭代两种实现方式,这里我给出上图二叉树三种遍历的递归代码:
/*
后面二叉树节点无特殊说明默认都是这种结构
type TreeNode struct {Val intLeft *TreeNodeRight *TreeNode
}
*/// 前序遍历上图种的二叉树
func preTraverse(root *TreeNode) {if root == nil {return}fmt.Println(root.Val)preTraverse(root.Left)preTraverse(root.Right)
}// 中序遍历上图种的二叉树
func midTraverse(root *TreeNode) {if root == nil {return}midTraverse(root.Left)fmt.Println(root.Val)midTraverse(root.Right)
}// 后序遍历上图种的二叉树
func postTraverse(root *TreeNode) {if root == nil {return}postTraverse(root.Left)postTraverse(root.Right)fmt.Println(root.Val)
}
二叉树与递归(重头戏)
这里我们就开始把二叉树和递归联系起来讲解。我个人的理解是二叉树和递归没有本质上的联系,只不过我们通过使用递归作用到二叉树上后可以更直观地研究和学习递归,就像显微镜和细胞的关系一样。
上面我们给出了二叉树的三种顺序的递归遍历代码,接下来我再用图文的方式详细讲解一下。
假如现在我们有一颗二叉树bTree,我们在遍历它的时候这样做:
func traverse(bTree *TreeNode) {if bTree == nil {return}fmt.Println("红")traverse(bTree.Left)fmt.Println("绿")traverse(bTree.Right)fmt.Println("蓝")
}
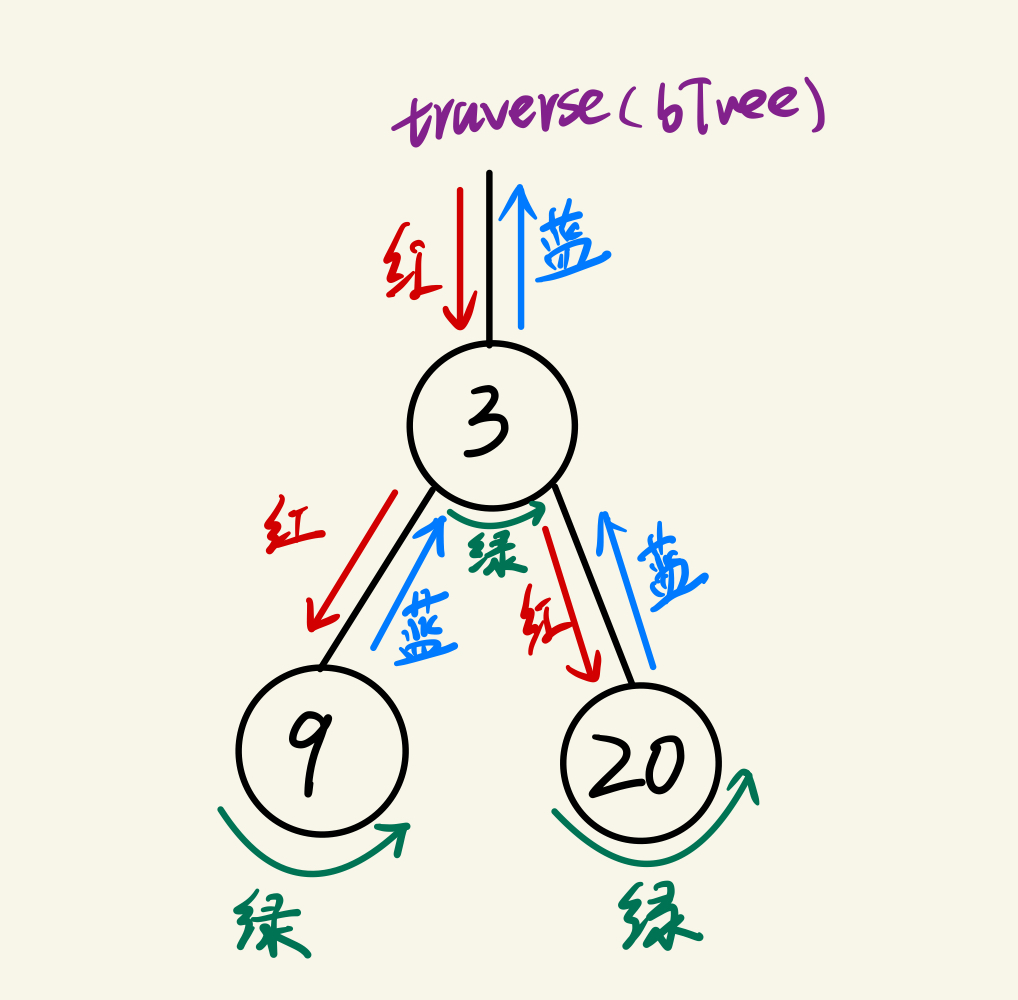
我们拿图中Val=9的节点来说明。
(1)调用traverse(bTree),这里算是第一层递归。bTree不为空,执行fmt.Println("红"),
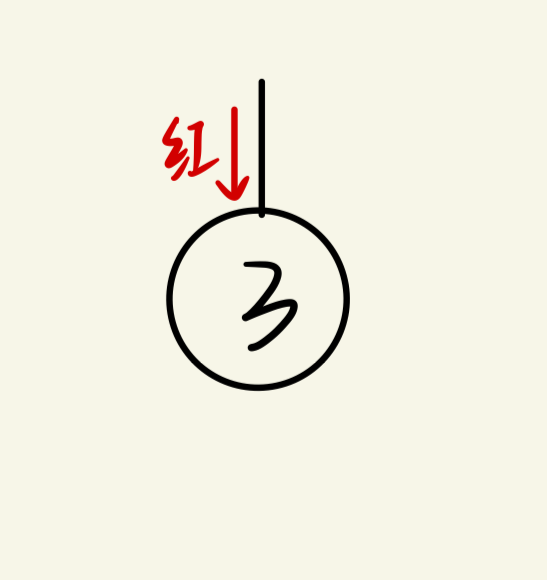
(2)执行traverse(bTree.Left),这里便会进入第二层递归,bTree的左子节点不为空,执行fmt.Println("红"),
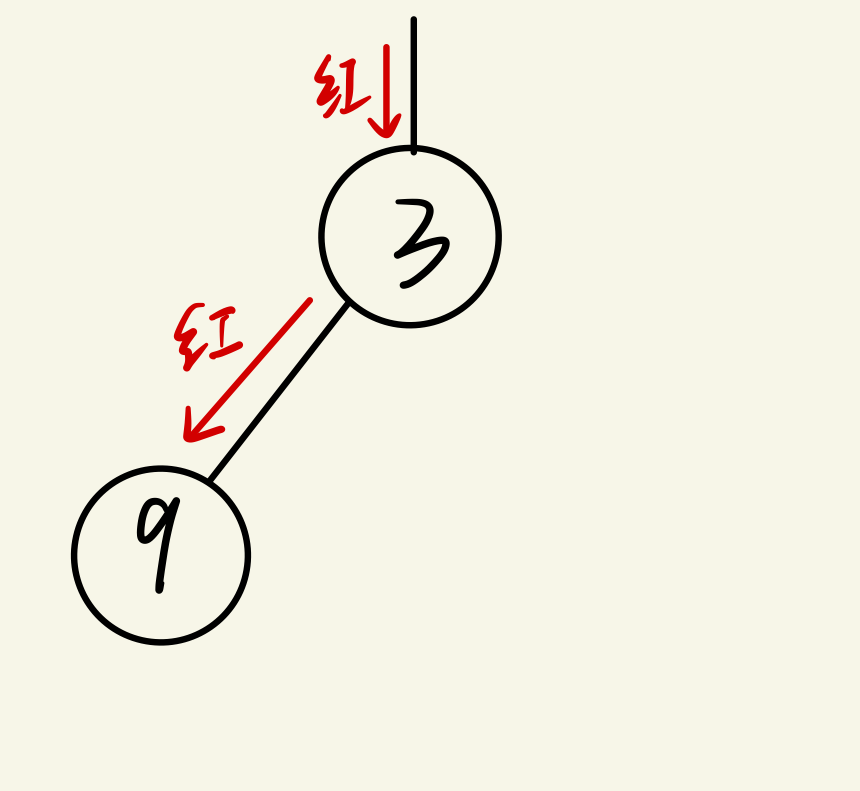
(3)执行traverse(bTree.Left),这里便会进入第三层递归,但是bTree不再是根节点,而是根节点的左子节点,也就是bTree.Left,所以这里其实可以看作是执行了traverse(bTree.Left.Left)。但bTree.Left.Left是空的,触发base case,也就是满足了 if bTree == nil 的条件,直接return,第三层递归退出,
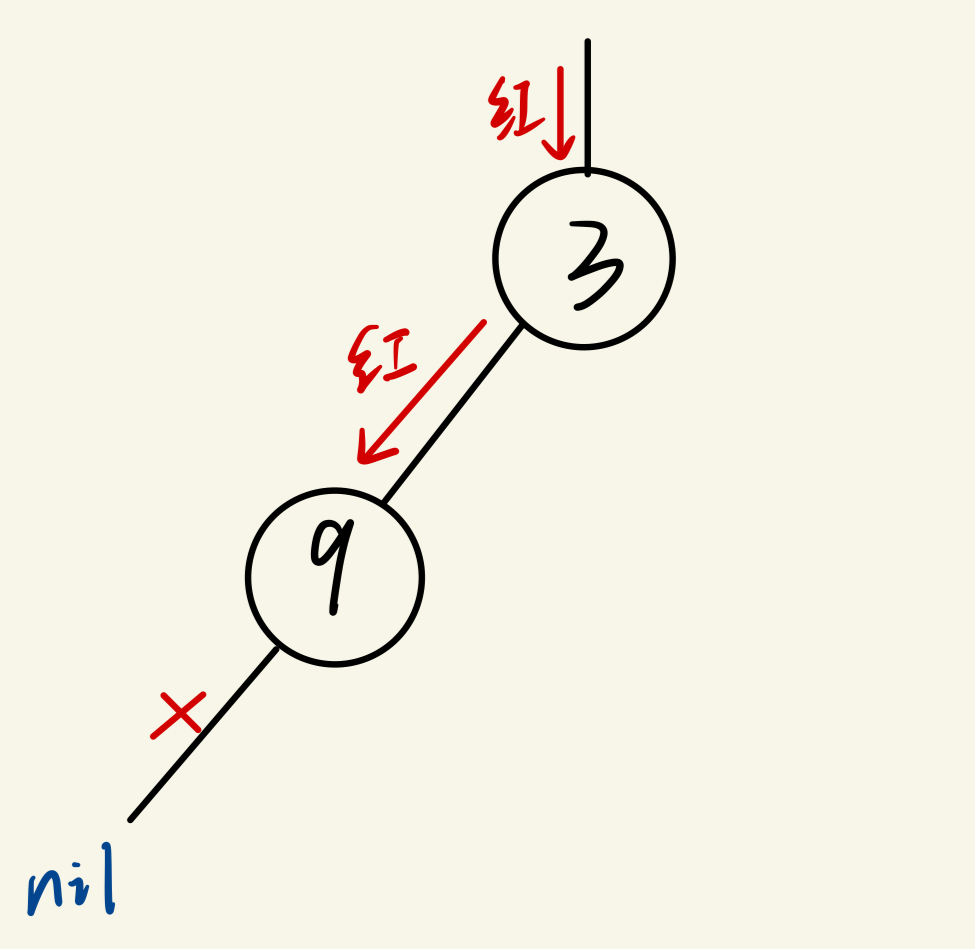
(4)traverse(bTree.Left.Left)结束后,会执行第二层的fmt.Println("绿"),即traverse(bTree.Left)后的fmt.Println("绿"),
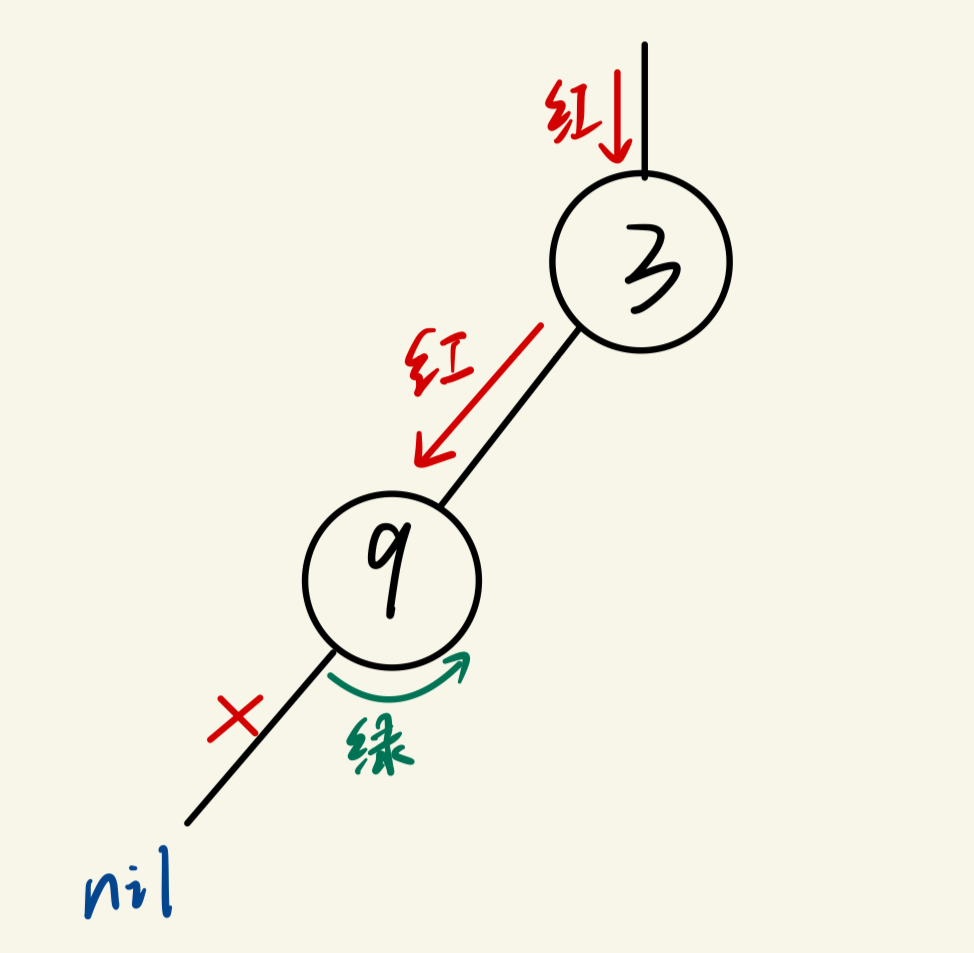
(5)执行第二层递归的traverse(bTree.Right),即traverse(bTree.Left.Right)这一行。也就是继续遍历bTree.Left的右子树,但其右子树也是空的,所以触发base case直接return掉,
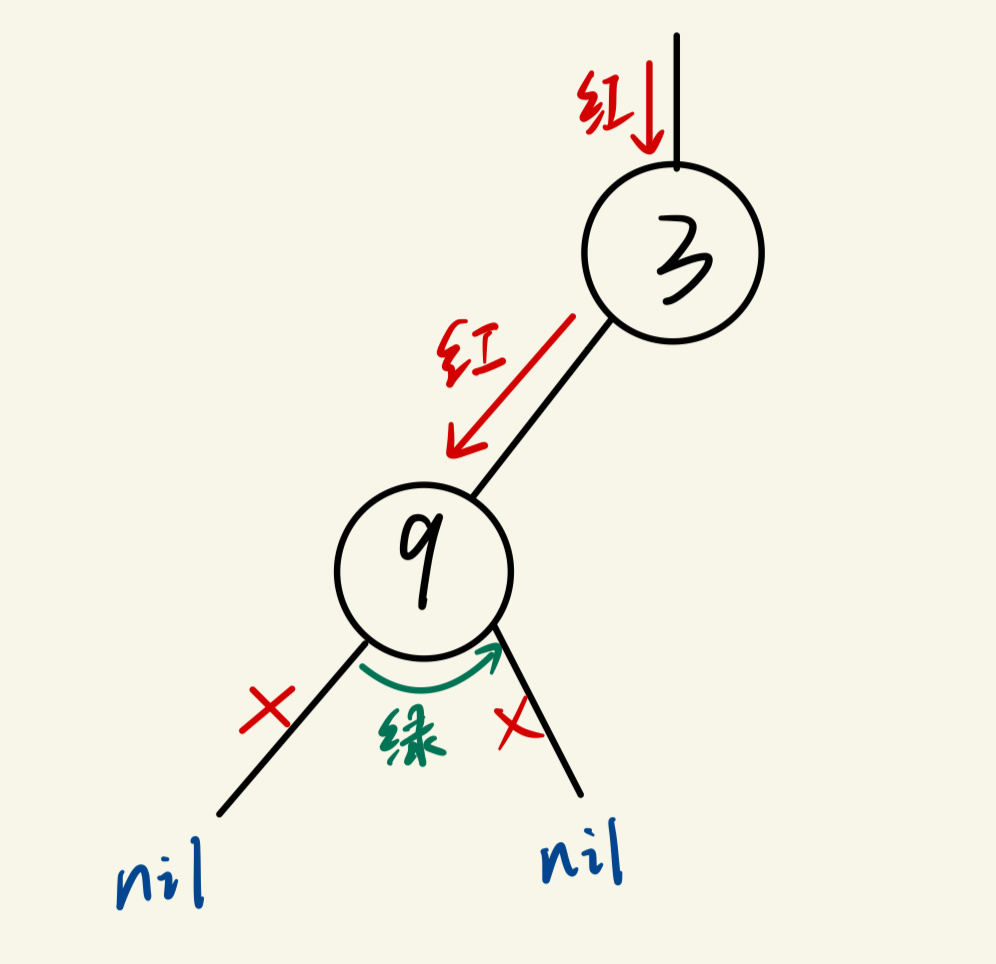
(6)到这里bTree的左右子树都已经遍历完成,即traverse(bTree.Left.Left)和traverse(bTree.Left.Right)都已经执行结束,接下来执行第二层递归的fmt.Println("蓝"),然后第二层递归结束,
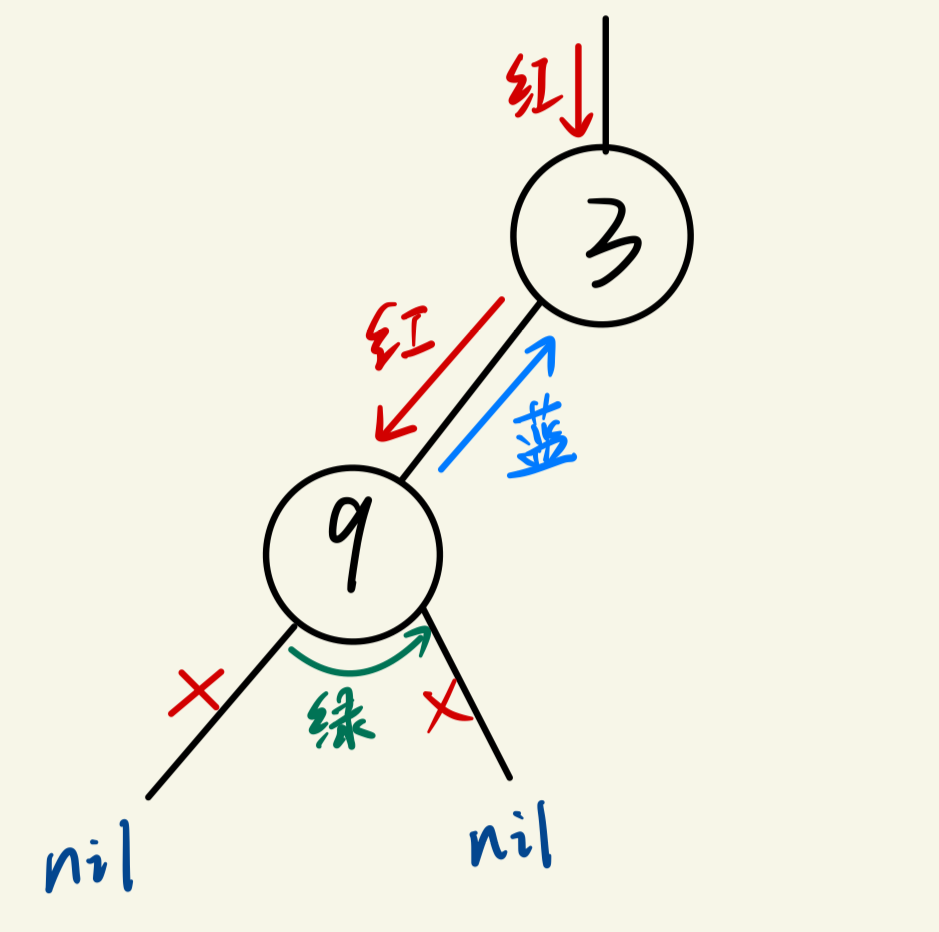
(7)第二层递归结束,这样我们已经遍历完了bTree的左子树,即traverse(bTree.Left)执行结束了,接着执行下一行,也就是第一层递归的fmt.Println("绿"),
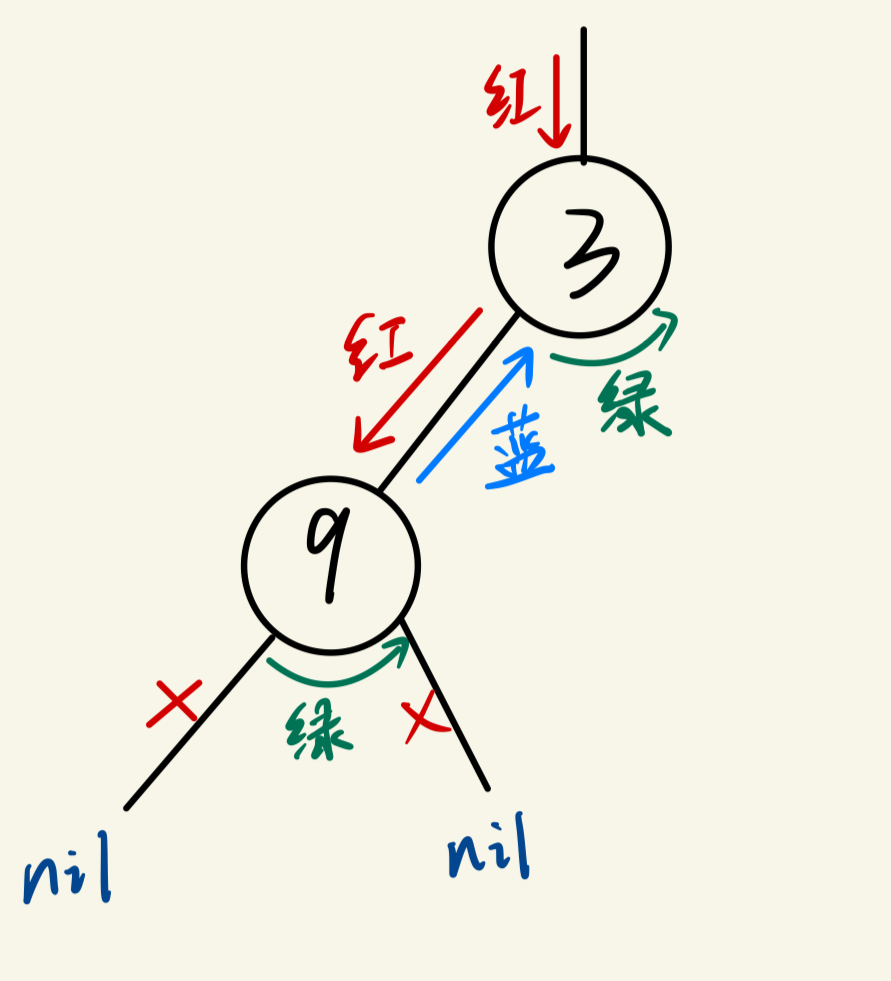
(8)执行第一层递归的traverse(bTree.Right),即开始遍历bTree的右子树,又会产生一个新的第二层递归,而traverse(bTree.Right)的遍历和traverse(bTree.Left)是一样的,只不过他的子节点比bTree.Left,但抛开整体看局部,其实都是一模一样的流程,所以后面的我就省略不画了,有兴趣的可以自己画一画,挺有意思的。
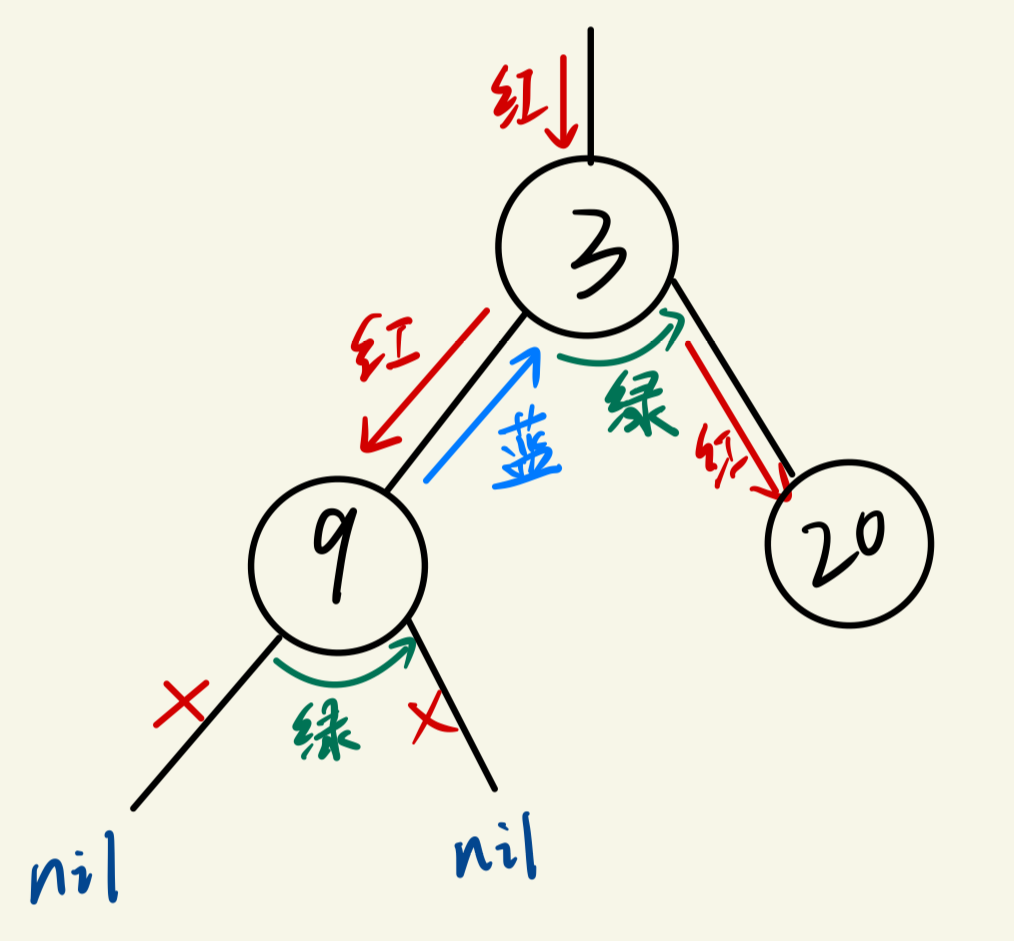
其实说到这里,大部分人肯定还是一脸懵逼,依然看不出二叉树和递归的关系,先别急。我们现在再看菲波那契数列的代码,
func fib(n int) int {if n < 2 {return n}return fib(n - 1) + fib(n - 2)
}
我们把这段代码画蛇添足一下,定义两个变量n1和n2分别来存储fib(n - 1)和fib(n - 2)的值,
func fib(n int) int {if n < 2 {return n}n1 := fib(n - 1)n2 := fib(n - 2)return n1 + n2
}
有没有觉得这段代码有一点眼熟?如果没有,那我再改一下,
func fib(n int) int {if n < 2 {return n}left := fib(n - 1)right := fib(n - 2)return left + right
}
元芳,这次你肯定发现了盲点。是的,这不就是二叉树的递归遍历吗?顺着这条逻辑,我们是不是可以推出:求解菲波那契数列的过程其实可以画出一颗二叉树!!!说画就画
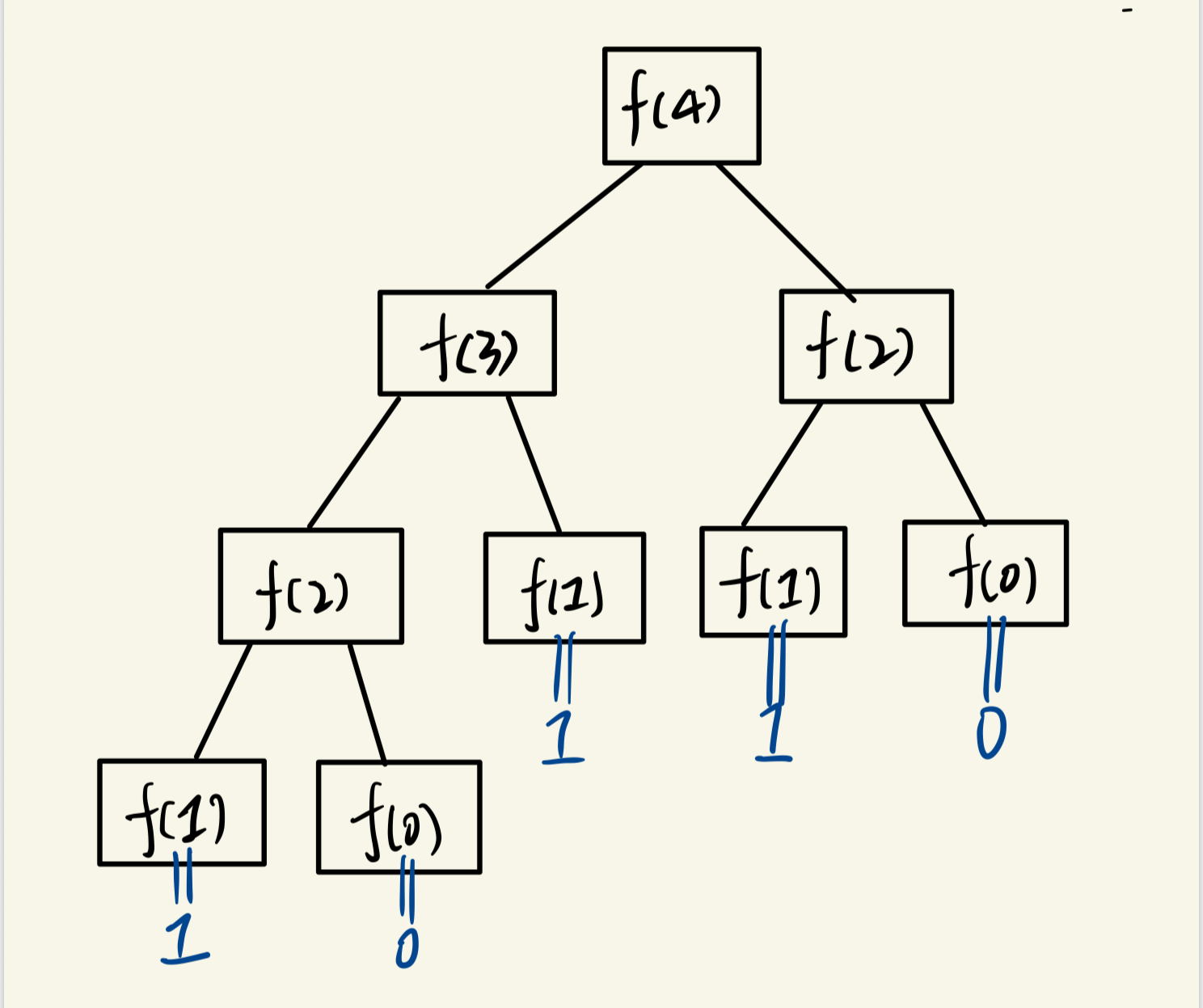
what the f...stop!这还不是最终形态,这只是超赛一形态罢了,接着我们直接超赛二形态,
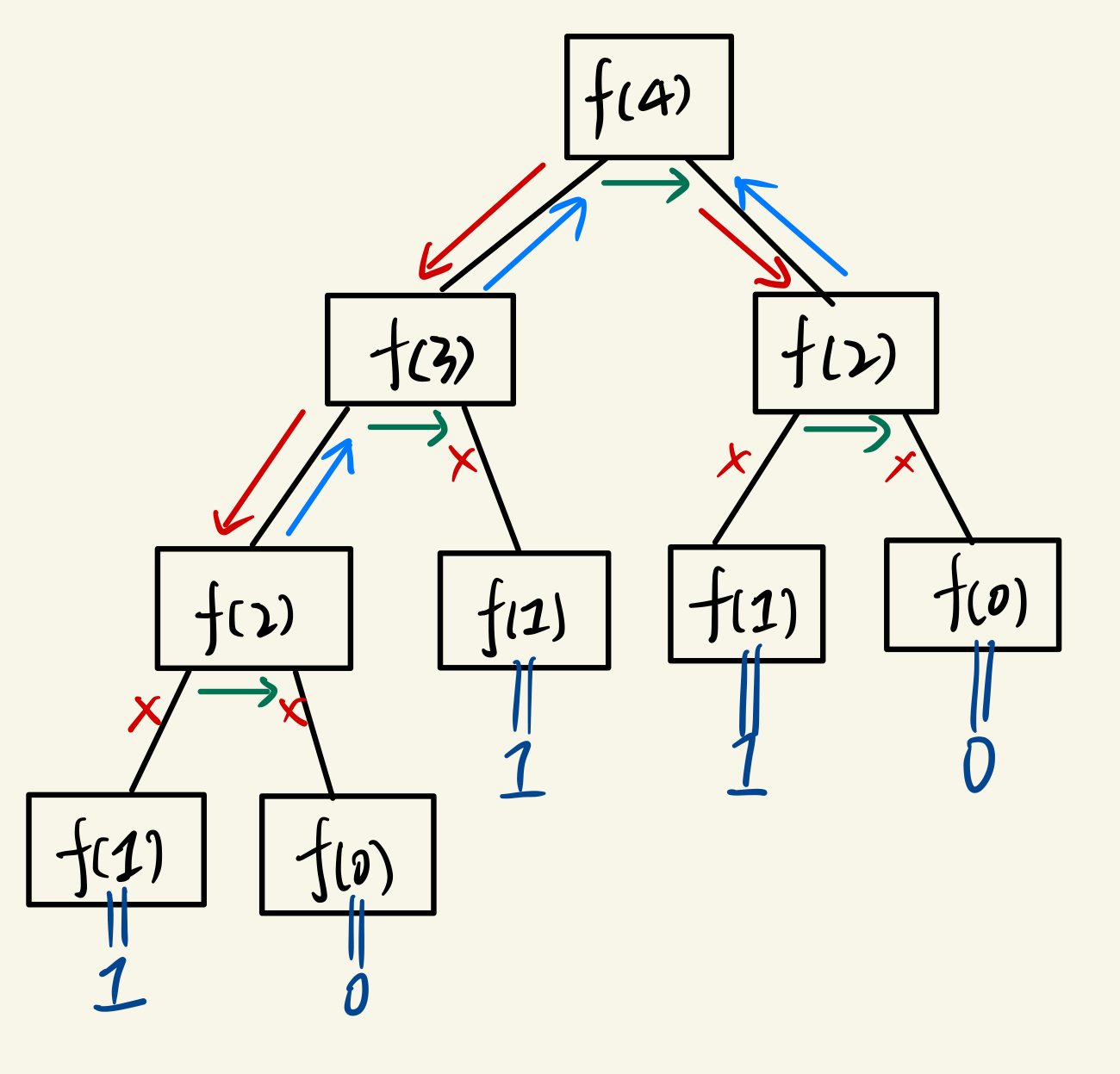
what the f***。好,其实很简单,你把上面我们遍历二叉树的过程带入到这里分析菲波那契数列就会豁然开朗。
总结一下,二叉树递归遍历的核心就是上面红、绿、蓝三条线,这三条线的位置分别对应树中节点前、中、后三个位置,你具体想做什么,就把代码写在哪个位置。比如,你如果想求某棵子树节点值之和的最大值,那最好的操作位置就是后序位置,现在你已经获取到了该节点的左右子树的信息,那么你就可以对比他们的节点值之和来获取到最大的那个。
注意!!!请大家牢记菲波那契数列这个图,因为这个图后面还可以用来理解动态规划,是的,虽然菲波那契数列本身并不具备最值特性,但是他的求解过程和求解动态规划问题及其相似!!!(这也是东哥的一篇神文提到的,大家可以直接去看他的文章)。
回文链表
接下来拿一道简单题练练手.
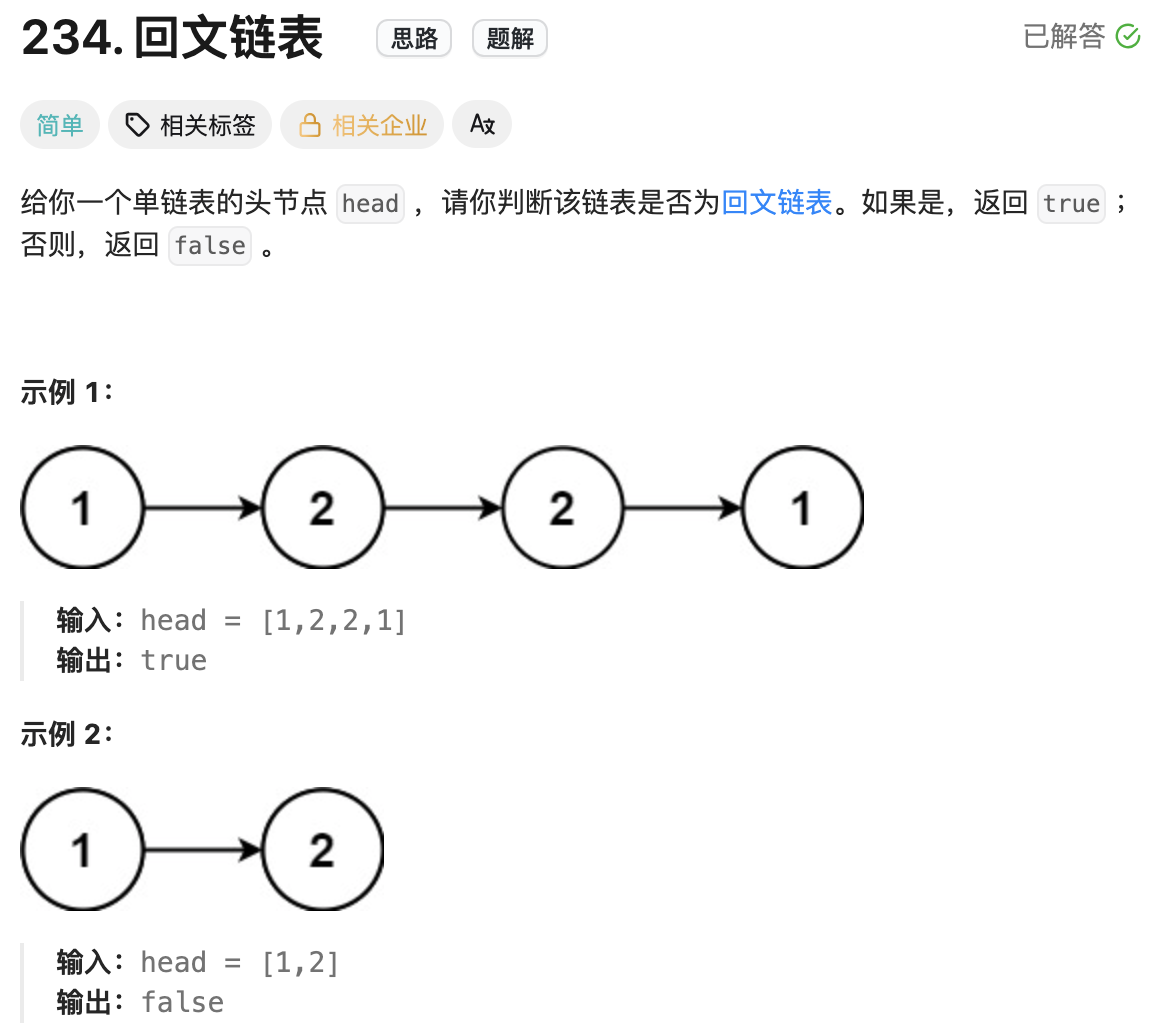
这道题实现方法有很多,最容易想到的是生成一条新的反转链表,然后用双指针从两个链表头开始遍历每个节点比较。这个算法还有一个巧妙的解法,那就是递归。
我们拿题目给出的这个链表来看,
emmm...平平无奇的链表,但是如果你抱起笔记本顺时针旋转45到60度再看一下,
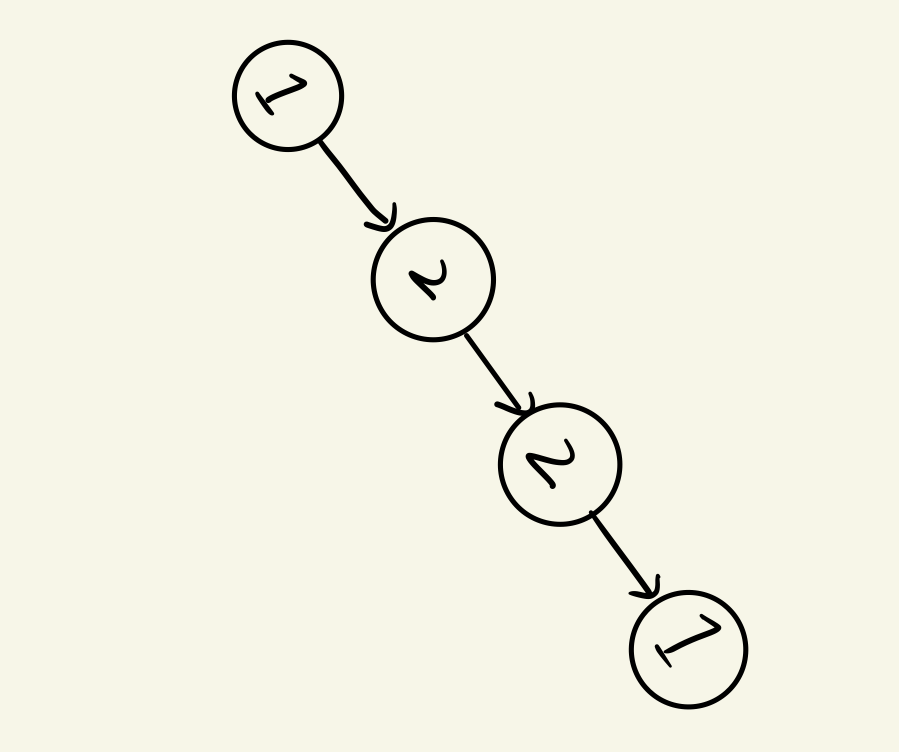
是不是很像某种我们刚才讲过的数据结构,然后我再改一下,
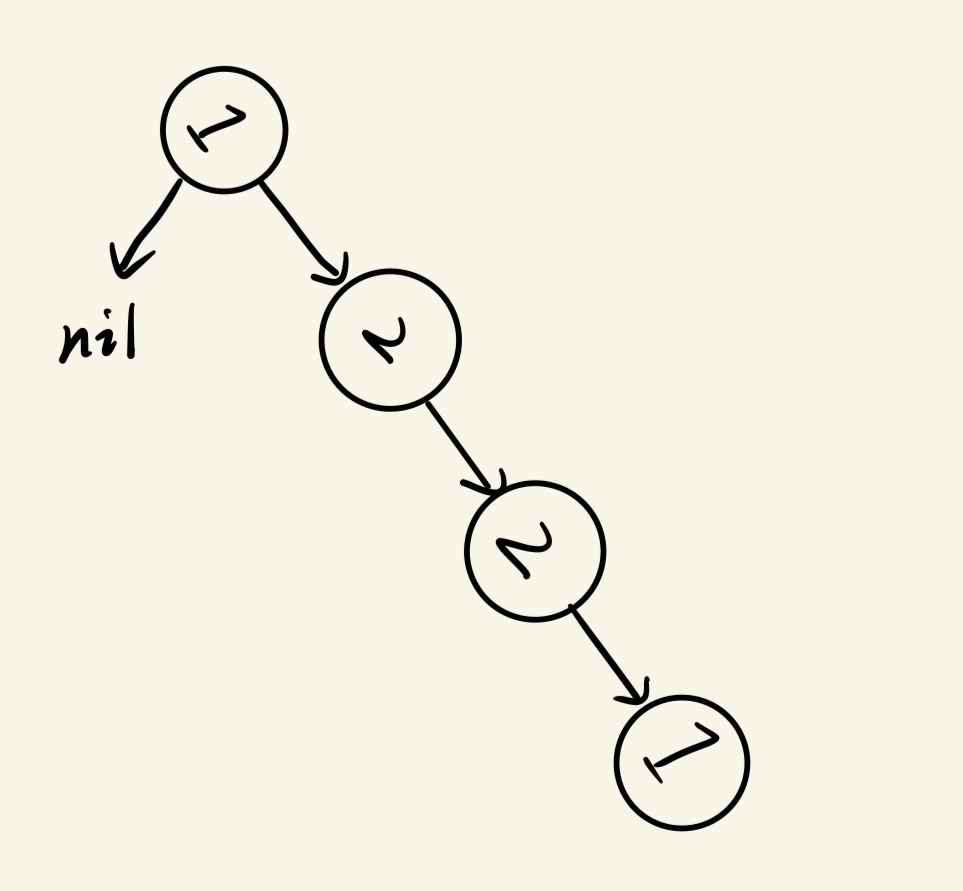
是的,其实链表就是一种特殊的二叉树,准确地说就是一棵根节点没有左子树的二叉树,那么,我们是不是可以用一个指针ASC指向链表头节点(也就是二叉树的根节点),然后通过遍历来倒序访问右子树的节点值呢?当然可以,只要我们在后序遍历的位置进行节点值访问即可。现在,我们可以倒序访问右子树,也可以通过ASC指针正序访问右子树,那我们就可以来验证链表是否为回文串,

代码如下:
/*** Definition for singly-linked list.* type ListNode struct {* Val int* Next *ListNode* }*/
func isPalindrome(head *ListNode) bool {asc := headvar res bool = truevar traverse func(desc *ListNode)traverse = func(desc *ListNode) {if desc == nil {return}traverse(desc.Next)if desc.Val != asc.Val {res = false}asc = asc.Next}traverse(head)return res
}
回溯
接下来,第二场重头戏来了。那就是用树的遍历来理解回溯算法,回溯的定义我就不说了,大家可以自己google或者问ai。我这里直接上例子说明。

全排列学过数学的都接触过,比如给你三个数1,2和3,给出所有可能的排列。按我们人类的思维,我们一般是这样的:
首先,第一个位置选择1,[1]
然后第二个位置我们有两个选择,2和3,我们先选择2,目前排列是[1,2],
最后第三个位置只剩3,那么我们得到第一个排列,即[1,2,3],
接着我们要生成第二个排列,我们人类的思维是可发散的,我们可以把第一个数改为选择2或者3,也可以把第二个位置改成3,可能脑容量大的哥们最后能得出正确答案,但我最后肯定乱掉,所以,我们最好是有逻辑的去组合这个排列。
比如我们在得到[1,2,3]后,我们可以把第二和第三个位置的数移除掉,这样排列就回退到[1],然后我们第二个位置不选择2,而是选择3,然后第三个位置只能选择2,这样我们就得到了一个新的排列[1,3,2],
再继续,这样一来1开头的排列就都得到了,然后我们再回退,这次我们把三个位置都移除掉,也就是回退到了空排列[],这个时候我们就可以重新选择第1个位置的数,这次我们选择2...
好,看到这肯定很多老哥已经快睡着了,无法直观的感受到树的遍历和回溯的有趣的地方,那动手画图来理解吧,就把前面选择1开头的排列过程画出来。
首先,来看一下我们目前手上的筹码吧,一个可选值列表 nums=[1,2,3],一个排列列表 permute=[],我们现在要做的事很简单,就是从 nums 中选择值放入到 permute 中,然后记录所有满足条件的 permute。那让我来一步一步地做吧。
(1)选择第1个位置的值。我们选择1,即 permute=[1],nums=[2,3]
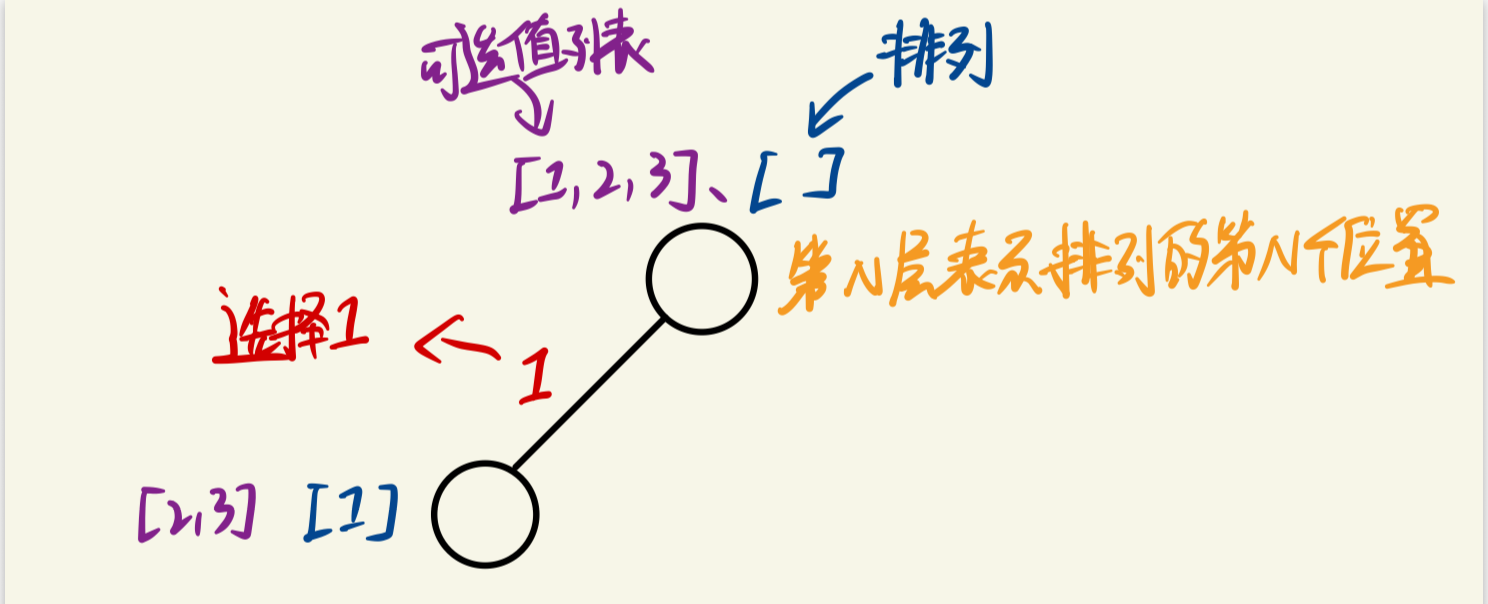
(2)选择第二个位置的值。我们选择2,即 permute=[1,2],nums=[3]
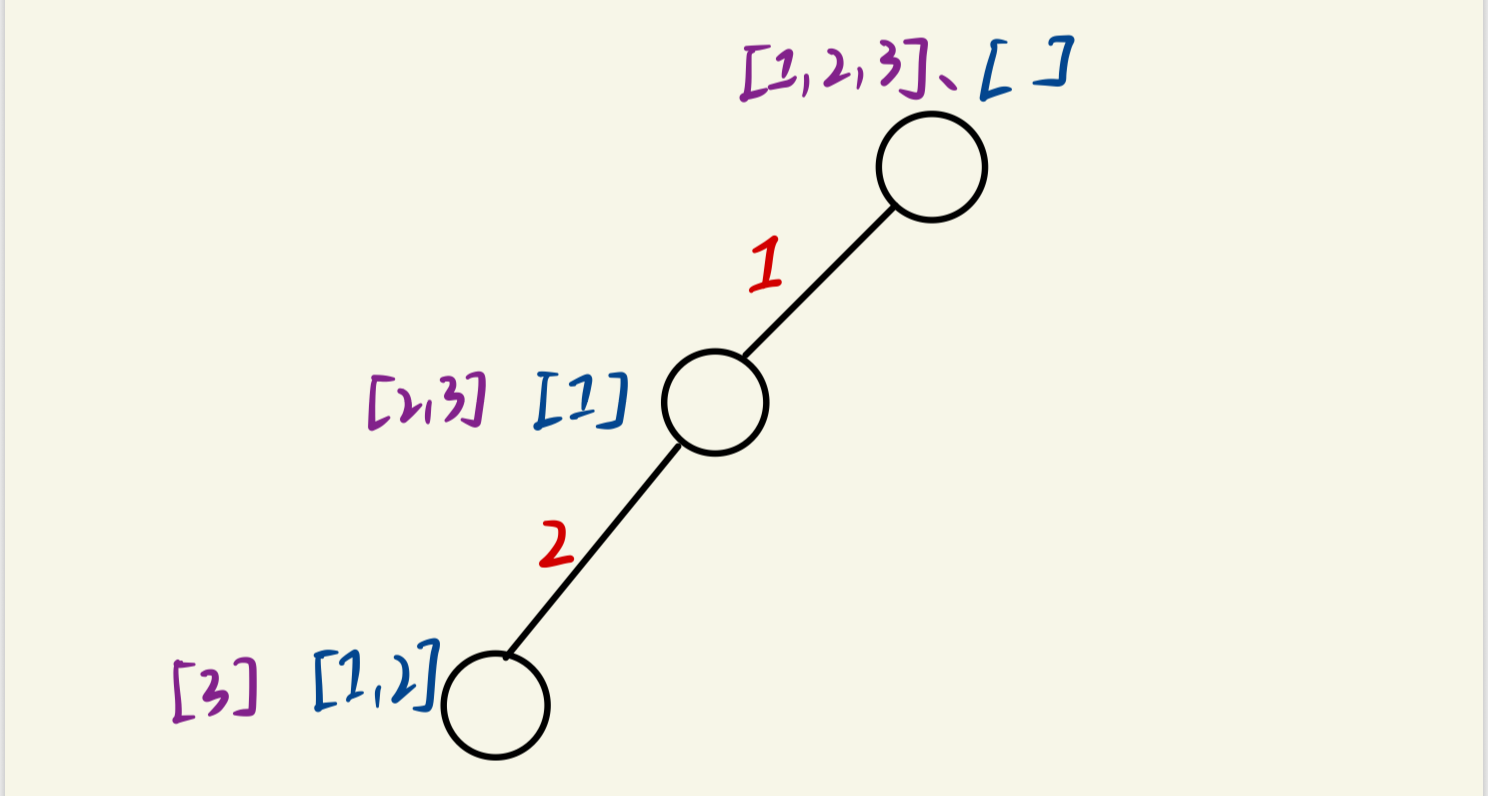
(3)选择第三个位置的值。我们选择3,即 permute=[1,2,3],nums=[],到这里,我们就得到了第一个全排列[1,2,3]
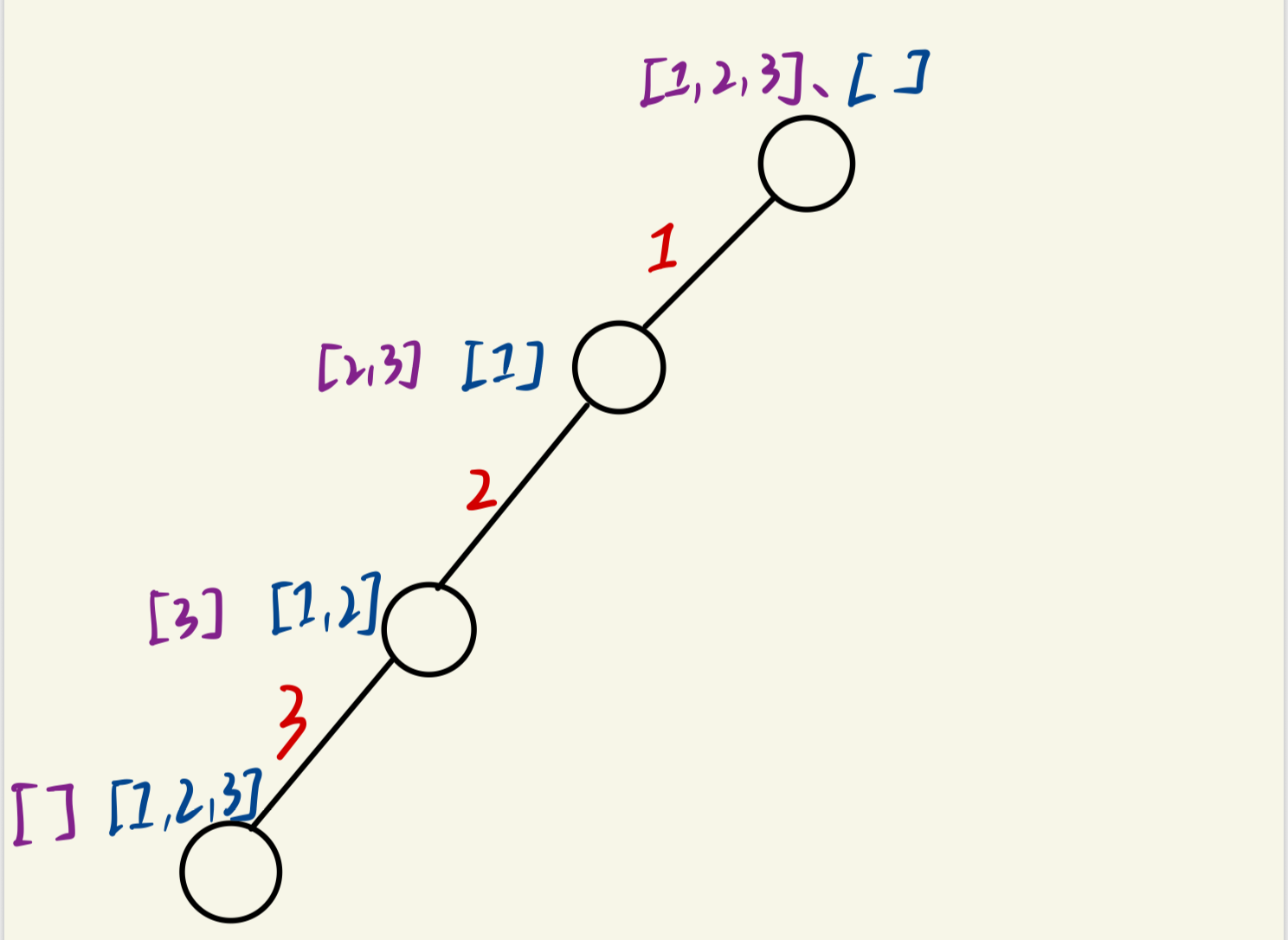
(4)接下来,就是最关键的一步,按我们上面说的要有逻辑的推导出全排列步骤,我们要把第三个位置的数移除掉,重新进行选择。首先,我们需要退到第三层的节点状态,这该怎么做?那就是在后序遍历的位置进行回退,即图中蓝色线部分,
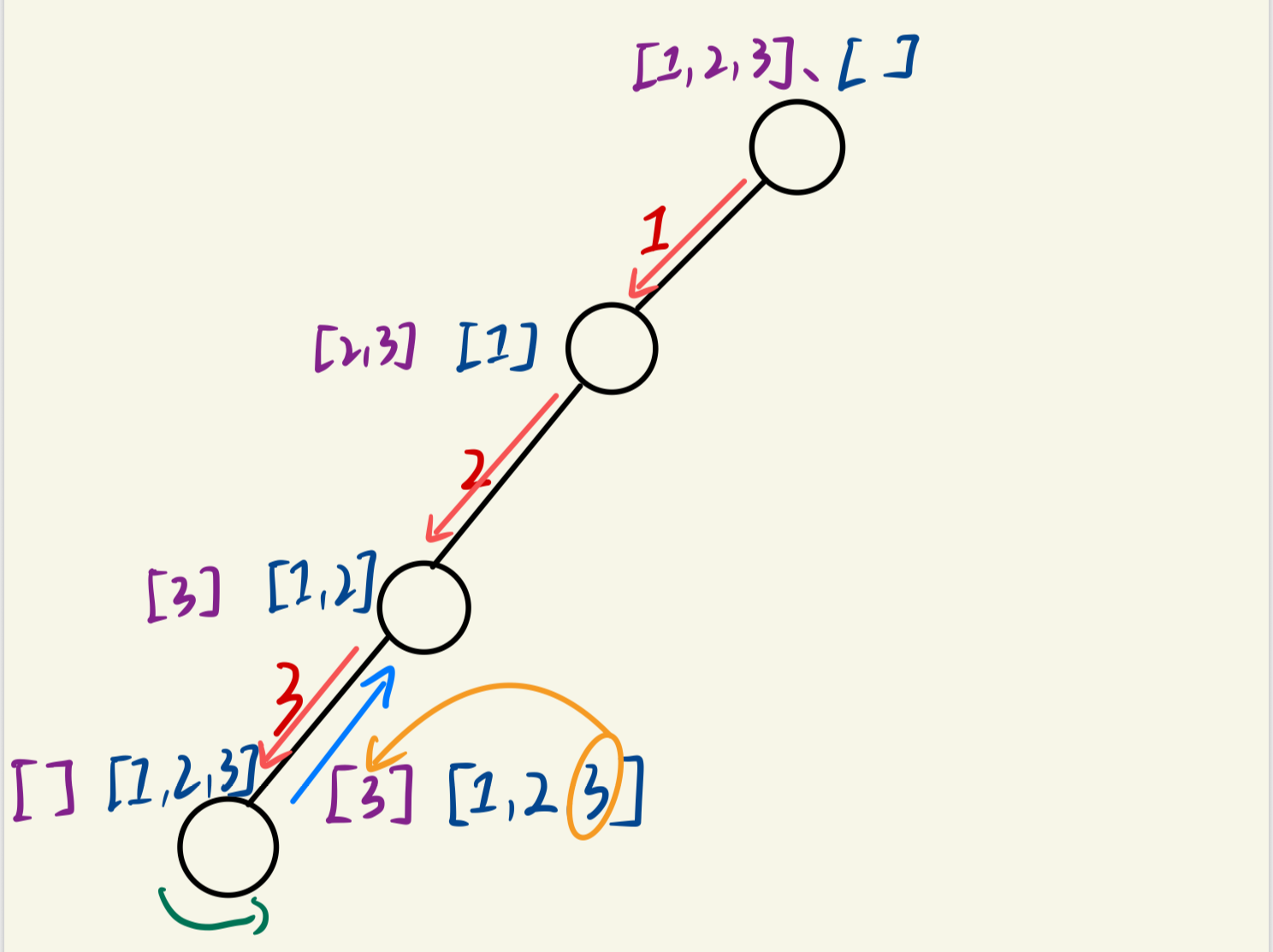
(5)经过上一步的操作,permute=[1,2],nums=[3],接下来我们移除第二个位置的数字,
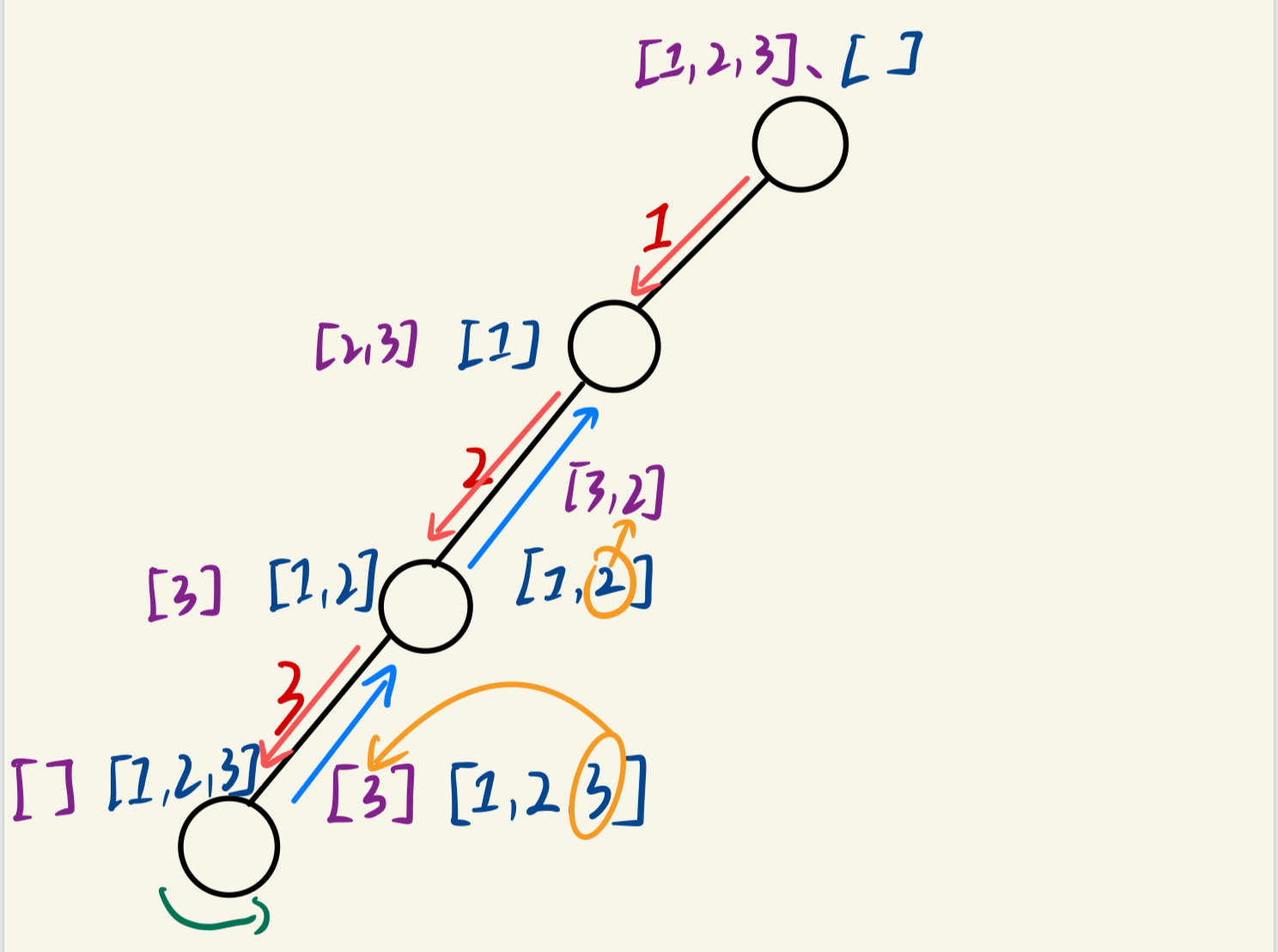
(6)现在,我们移除了第三和第二个位置的数字,即permute=[1],nums=[2,3],我们可以重新选择第二个位置的数字,这次我们选择3,
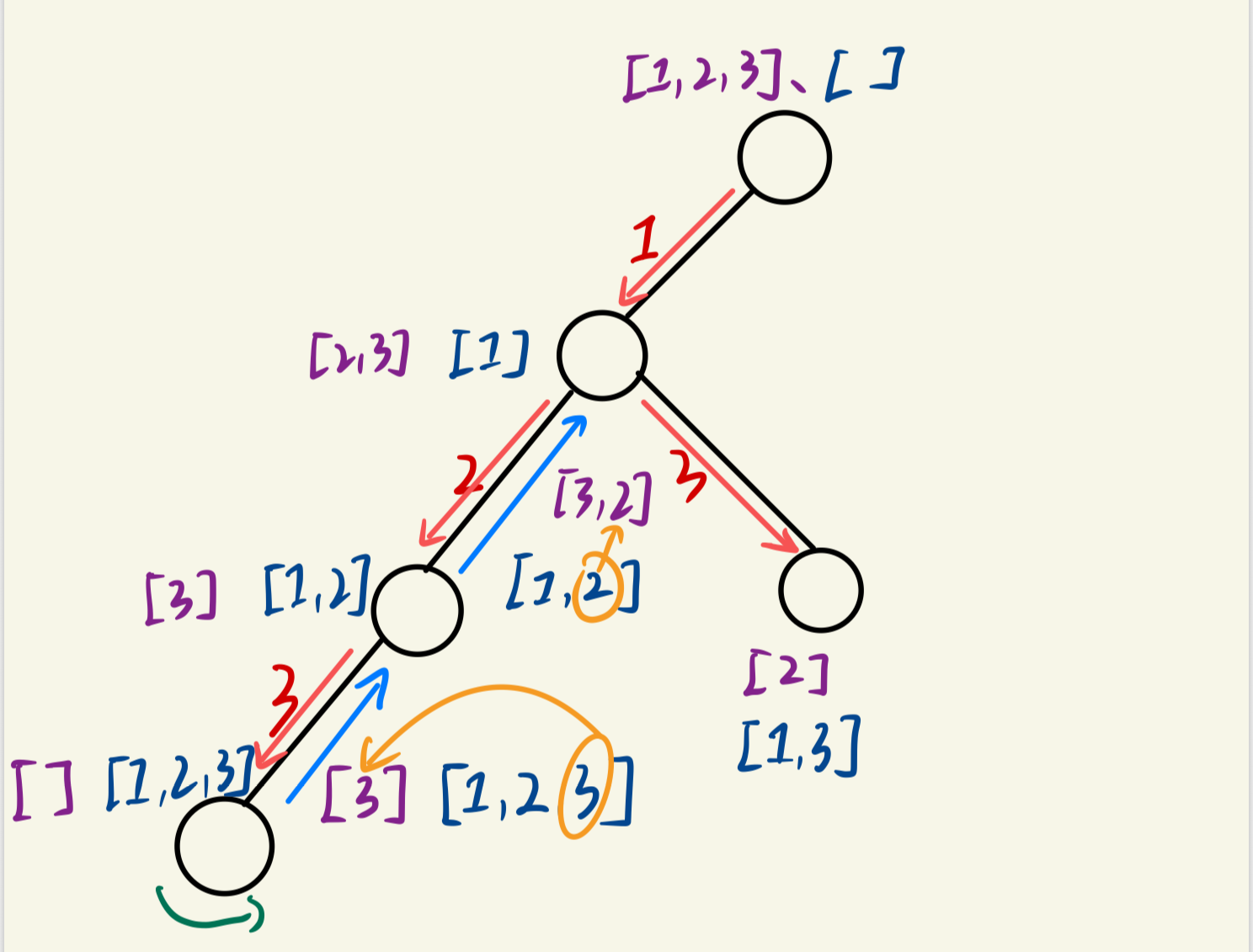
(7)再选择第三个位置的数字,即2,我们又得到了一个新的排列[1,3,2],
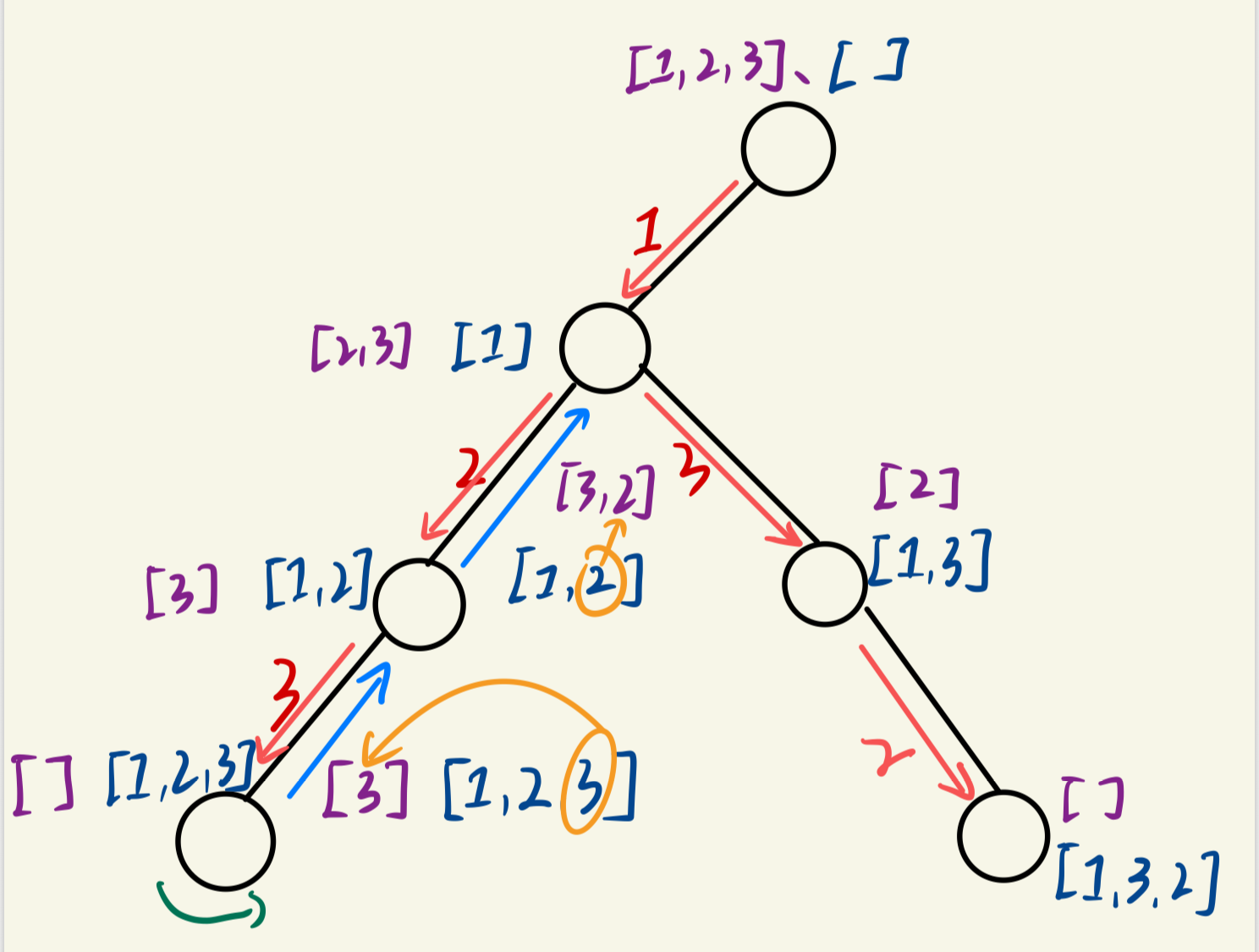
再后面会发生什么,我就不说了,大家可以自己慢慢品味。
当然,上面的图片只是大概的思路,要实现代码还是有很多细节要处理的,下面给出代码,大家可以自己跟着走一遍,
func permute(nums []int) [][]int {var res [][]intvar cur []intselected := make(map[int]bool)for i := 0; i < len(nums); i++ {selected[nums[i]] = false}var backtrack func(nums []int)backtrack = func(nums []int) {if len(cur) == len(nums) {tmp := make([]int, len(cur), len(cur))copy(tmp, cur)res = append(res, tmp)return}for i := 0; i < len(nums); i++ {num := nums[i]if selected[num] {continue}cur = append(cur, num)selected[num] = truebacktrack(nums)cur = cur[:len(cur)-1]selected[num] = false}}backtrack(nums)return res
}
递归、二叉树和动态规划(持续更新中...)
这一部分我会找时间做更新。以上我觉得算是二叉树和递归一个比较入门的讲解,讲解的题目也比较简单,大家可以更好的理解递归和二叉树,如果想进一步了解,大家可以去看labuladong的算法笔记,还有就是要多刷题,理解了和能写出代码完全是两个概念。
