网络计划图
概念
表示整个项目的网络图,成为项目网络。描述一个项目需要三方面的信息:活动、次序、时间。通常有两类网络:用弧表示活动的项目网络(双代号法,AOA);用节点表示活动的项目网络(单代号法,AON)。
AON中:
1、每个活动都用节点表示;
2、弧表示活动间的先后关系,从紧前活动指向它的紧后活动;
3、对有紧前活动的节点,每个紧前活动都各有一条弧指向它。
举例
【问题】A公司中标了一个价值540w的项目,这个项目有以下的活动构成,绘制它的项目网络图。
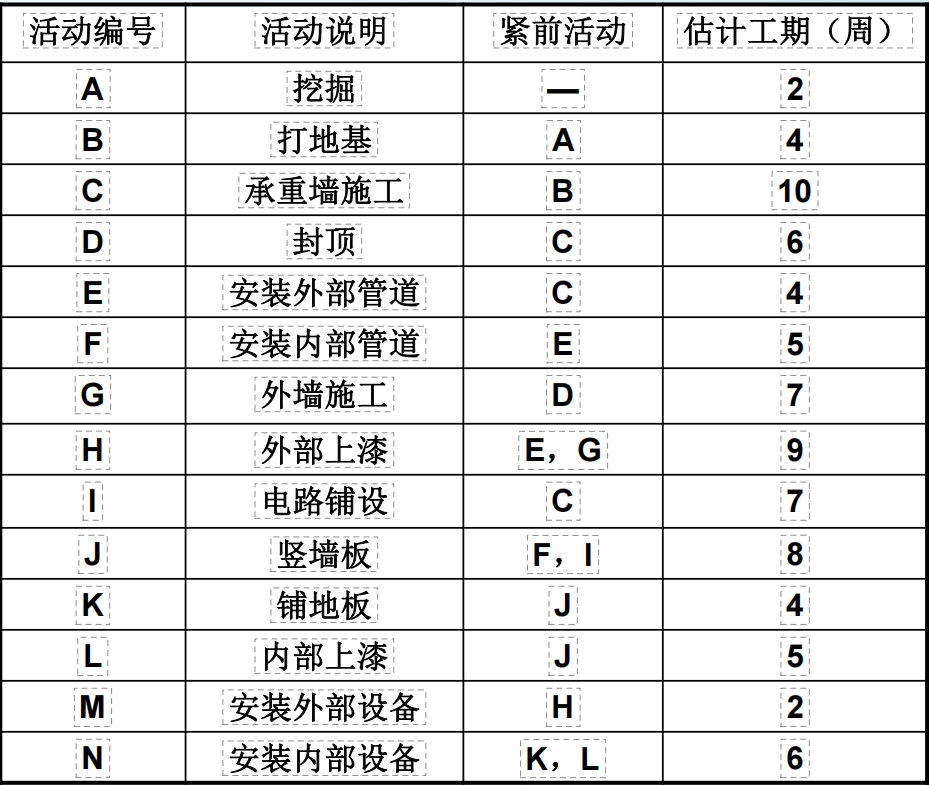
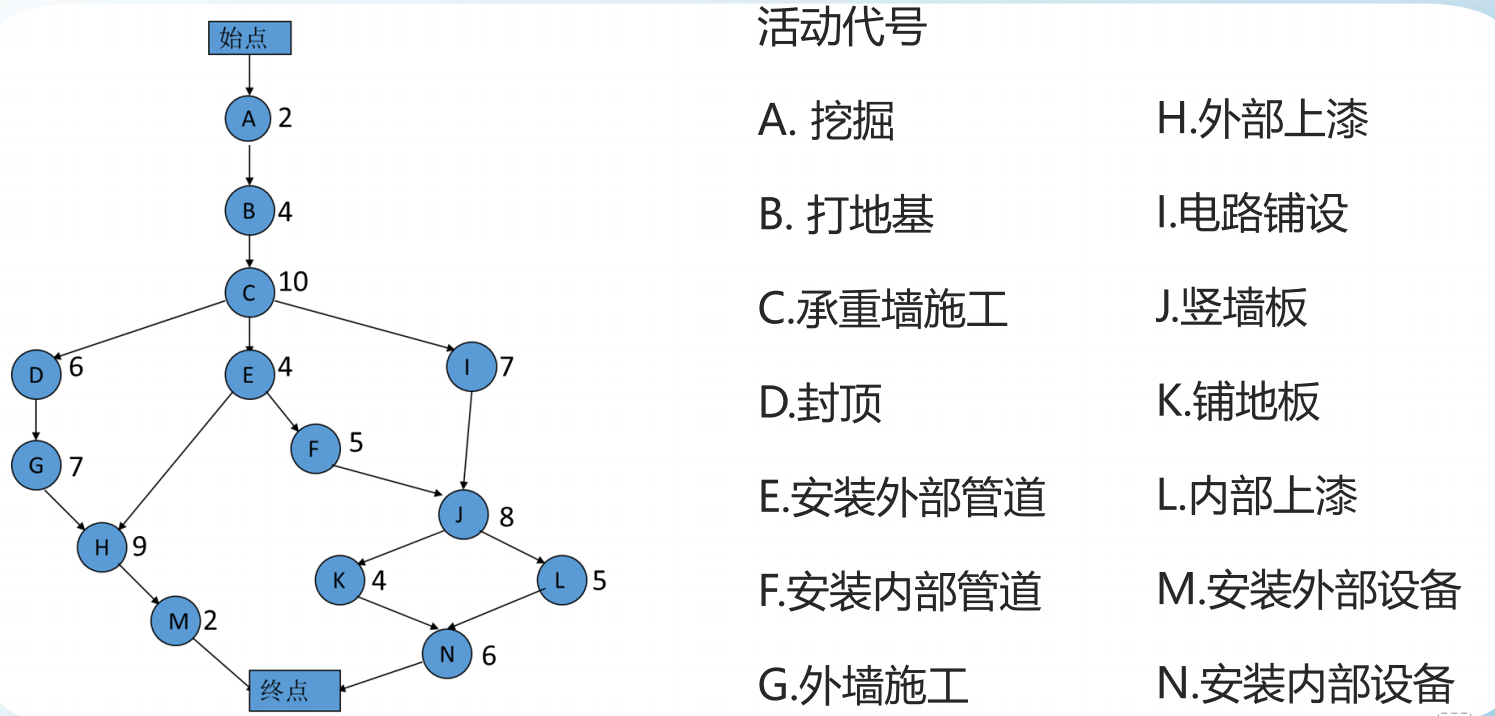
【解答】根据概念,先把每个有紧前活动的节点都画出来,并画出它的紧前活动。注意,要画出起点和终点。画图的时候,为了美观性,最好每一层级的节点放在同一层,比如DEI。
关键路径法(CPM)
概念
从起点到终点,沿着某条路径,计算此条路径的工期之和。工期最长的路径,就是关键路径。查找关键路径,有两种方法:
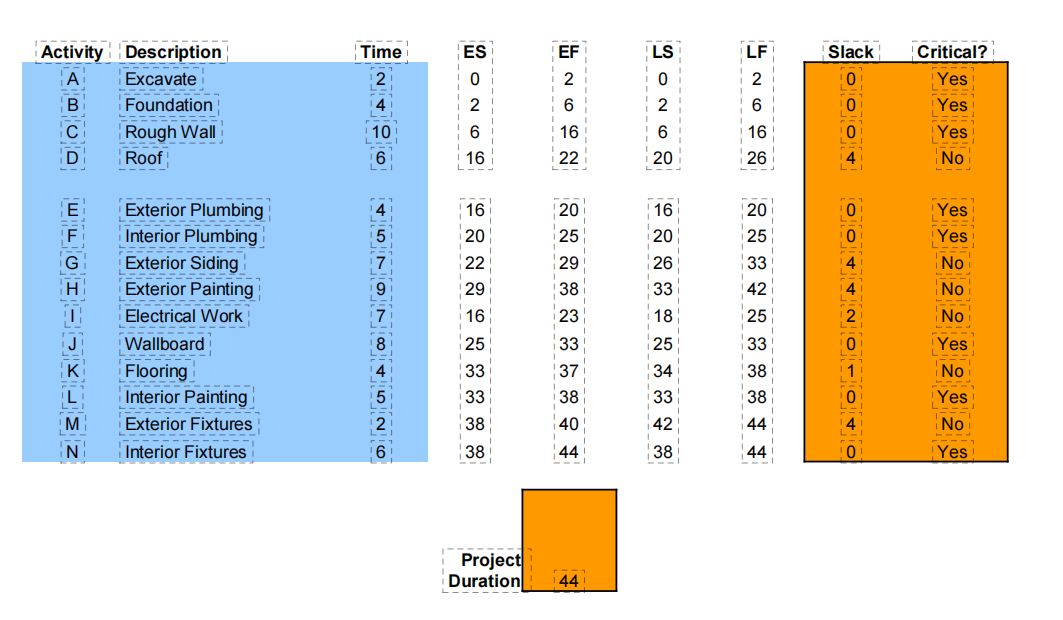
1、穷举法:每条路都算一下工期之和,最长的路径就是关键路径,比如上图有6条路径,最长的为“开始ABCEFJLN结束”,工期之和为44周;
2、时差法:把每个工序的最早开始时间(EST,起点的EST为0)、最晚开始时间(LST)、最早结束时间(EFT)、最晚结束时间(LFT)计算出来,得到每个工序的时差,即 每个节点的时差=最晚开始-最早开始=最晚结束-最早结束。在不延误总工期的前提下,可以理解为就是一个工序允许的buff时间。关键路径上的节点,时差为0,也就是没有任何buff给你灵活安排了。注意,终点的最早、最晚的开始、结束时间,都等于关键路径长度。其中,在所有工序均不延误的前提下:
1)(与其他节点有关【紧前工序】)最早开始时间=MAX此工序所有紧前工序的最早结束时间,即取决于紧前工序的最早结束时间。如果有多个紧前工序,就看谁结束的最晚,也就是所有紧前工序里面结束时间的最大值;
2)最早结束时间=最早开始时间+工序的时间 t ;
3)最晚开始时间=自己的最晚完成时间-自己的工序时间 t ,即最晚开始取决于你最晚什么时候必须结束;
4)(与其他节点有关【紧后工序】)最晚结束时间=MIN此工序所有紧后工序的最晚开始时间。如果有多个紧后工序,就看谁开始的最早,也就是所有紧前工序里面结束时间的最小值。
二者对比:
1、穷举法,需要遍历每条路径,最差的情况下,路径数量随节点数N的指数增加(O(N*2的N次方)。因为假如有 N 个节点(除去开始、结束),每个节点平均有 2 个分支,路径数就是 2的N次方,再乘以计算每条路径的成本,如果有N个节点,每个节点的计算用一个成本,近似看总成本就是 N。因此就得到 O(N⋅2的N次方) 的计算复杂度。),大规模问题下,效率较低;
2、时差法,计算出每个节点的EST、EFT、LST、LFT,然后得到开始和结束时间的时差,为0的节点会组成关键路径。算法耗时为O(N+E),N为节点数目,也就是工序数目,E是边的数目。就是每个节点算一下,每个边算一下。远比穷举法效率高,并且适合进行下一步延伸的研究。
举例
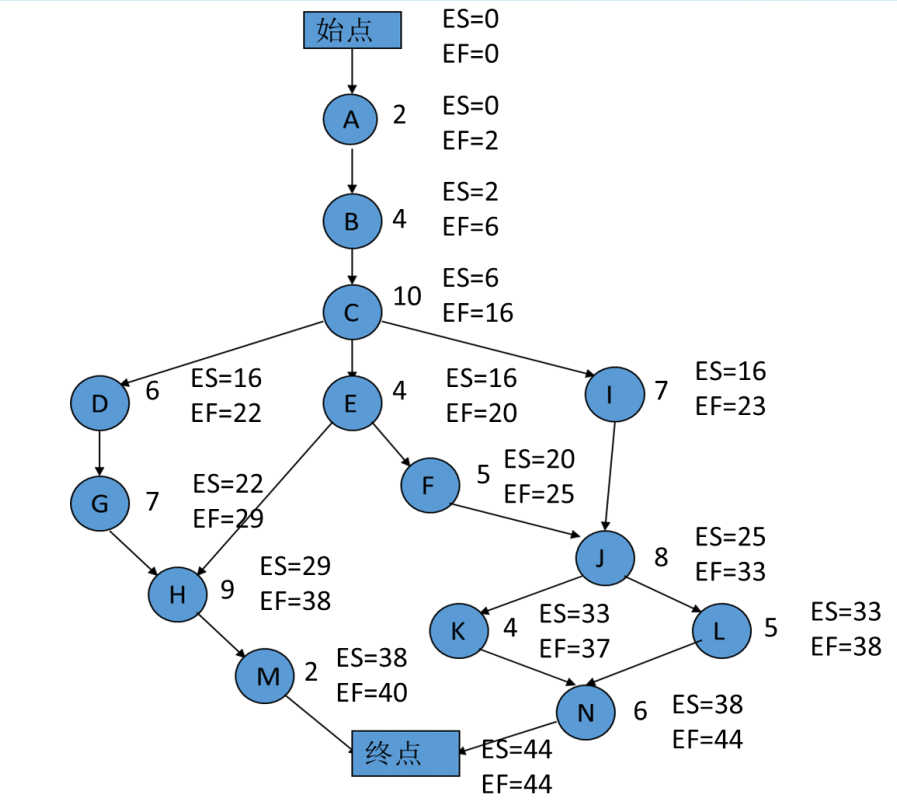
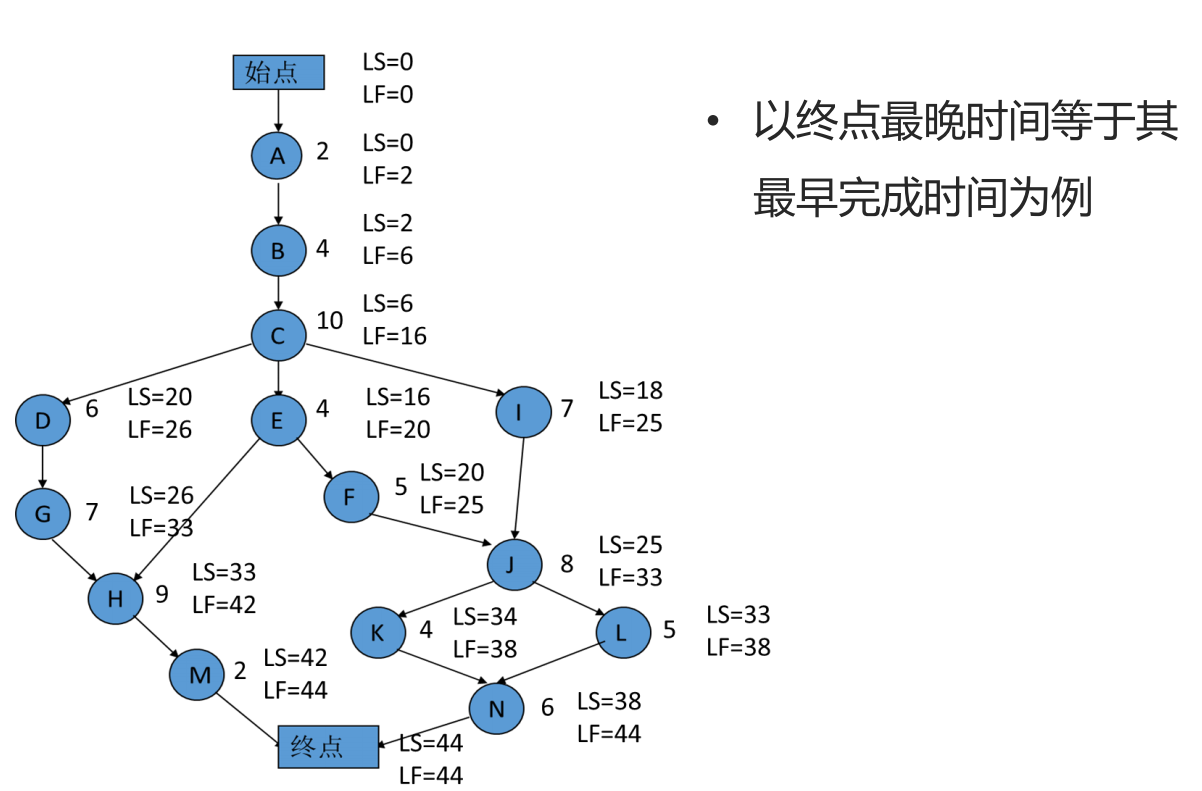
基于上面的网络图,可以得到每个节点的最早开始时间和最早结束时间,计算最早xx,都是从起点算:
基于上面的网络图,可以得到每个节点的最晚开始时间和最晚结束时间,计算最晚xx,都是从终点算:
基于上面的网络图,得到每个节点的时差情况,并判断是否处于关键路径:
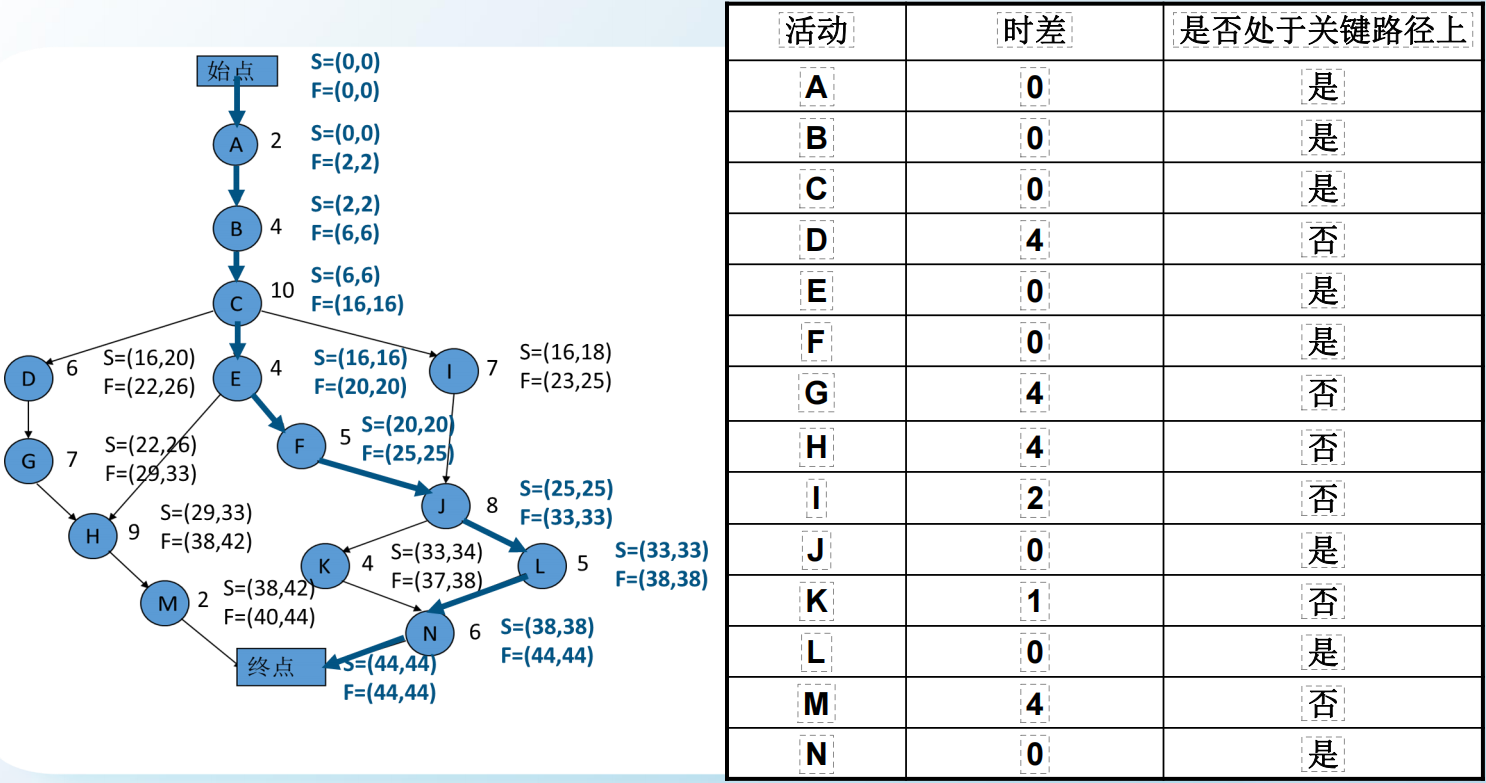
进而求得关键路径长度:
评估评审技术PERT
概念
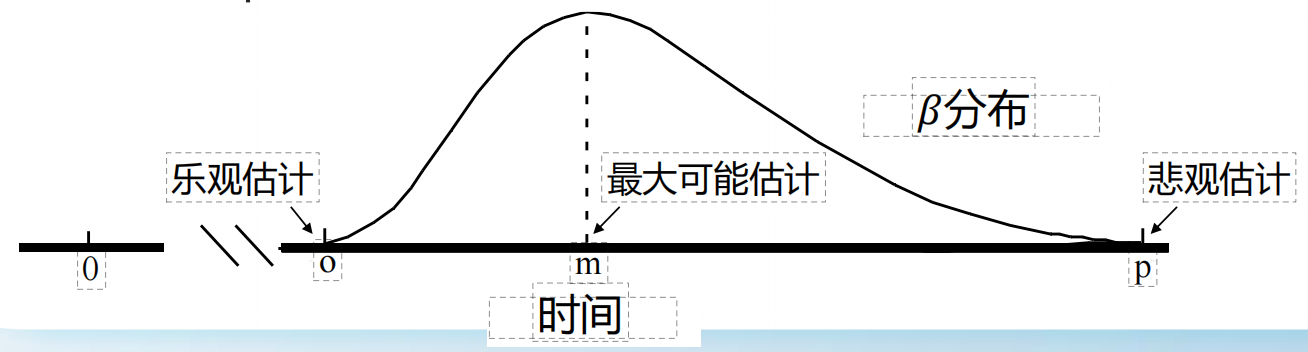
主要用于估计工期,以及按时完成的概率。具体设计到三个关键概念,这也就是PERT的三时估计:
1、最大可能估计(m)= 完成某项活动最可能的工期;
2、乐观估计(o)= 最佳条件下完成某项活动的工期;
3、悲观估计(p)= 最不利条件下完成某项活动的工期。
图像可能如下:
工期方差的近似估计:
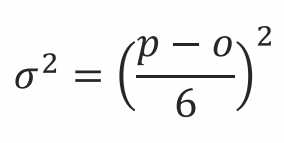
工期均值的近似估计:
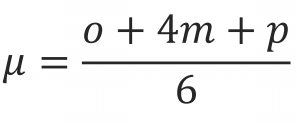
举例
基于上图,得到的三时估计和方差、均值计算如下:
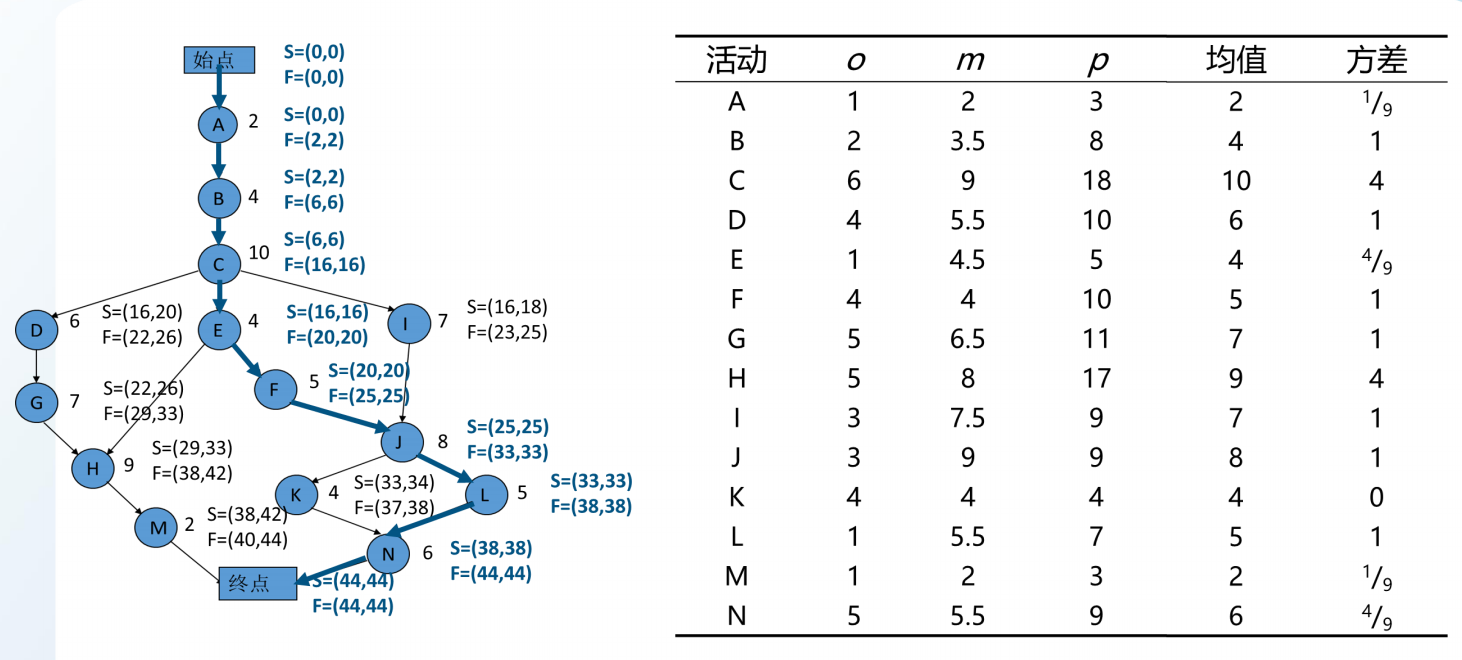
基于每个节点的均值工期,计算到的关键路径,就是均值关键路径。如果满足以下三个假设,则均值关键路径的工期之和,就是项目工期的均值。均值关键路径的方差之和,就是项目工期的方差。
1、假设1:均值关键路径是项目网络中,最长的一条路径;
2、假设2:均值关键路径的活动工期,具有统计独立性;
3、假设3:项目总工期的概率分布,为正态分布。
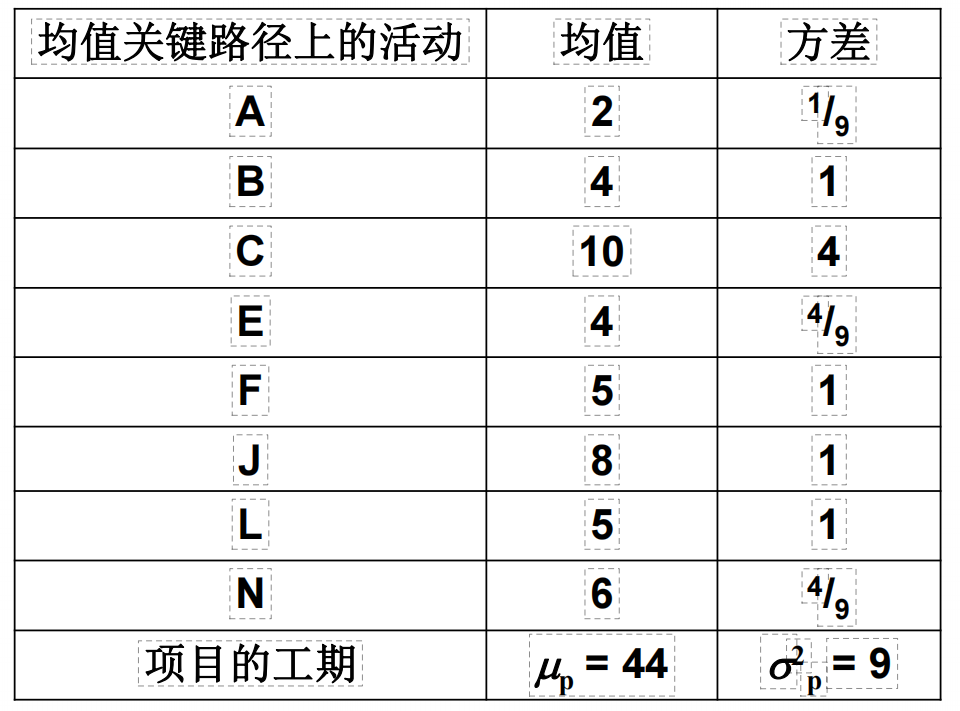
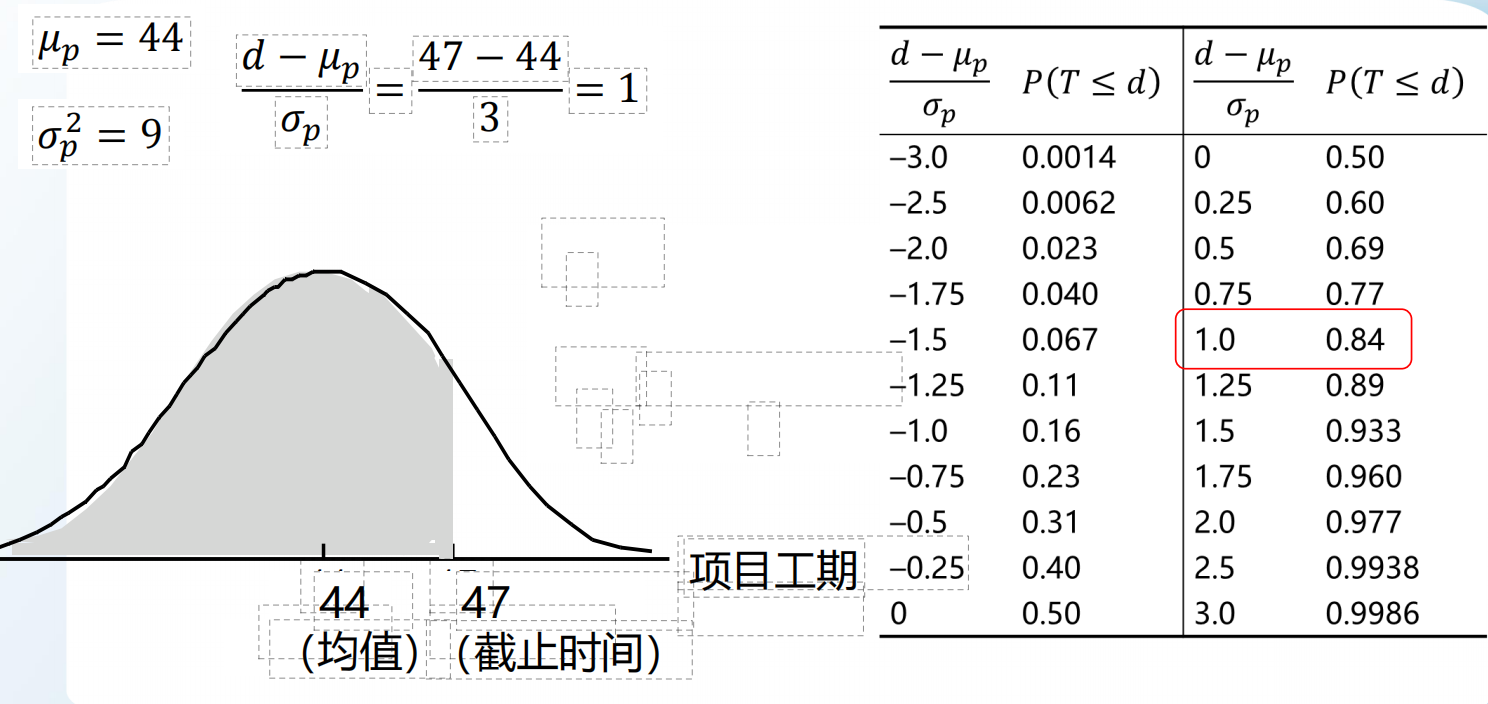
假设,在这个例子中,要求最长使用的工期只有47周,那么要想44周就完成的概率,就是 根据 要求的最长工期-项目的使用工期/项目标准差 求得的结果,再对比 标准正态分布的概率查询表 ,得到概率情况,即如果44周完成,概率是84%.(注意,这个表格代表的意思是:如果假定计划工期是47,平均工期如果是48,那就用左边比较(也就是算出来是负数);如果假定计划工期是47,平均工期如果是44,那就用右边比较(也就是算出来是正数)。)
项目时间与成本管理
概念
应急完成一项工序,是指,通过某些高费用的特殊途径,把活动的完成时间减少到正常水平之下。比如加班、雇佣临时工、使用一些特殊的省时材料或省时设备等。
应急完成项目,是指,对其中的一些活动,进行 应急处理,把工期缩短到正常值以下。
时间成本平衡的CPM方法:
1、应急处理关键路径上的活动,并考虑时间和成本的平衡问题;
2、优先应急处理关键路径上,边际应急成本最低的活动;
3、在不断地应急处理过程中,关键路径可能会变化。

举例
假设,基于上面的项目情况,我想用最低的成本,把项目总工期压缩到40周,应该怎么做呢?应急的成本对应表如下:
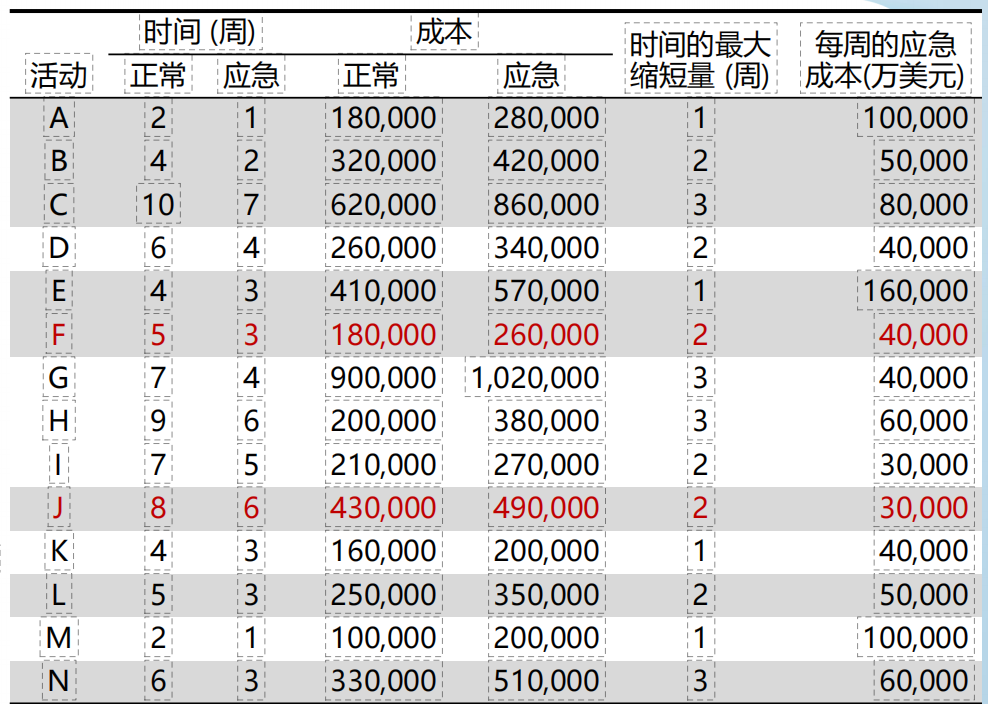
当前关键路径如下(红色):
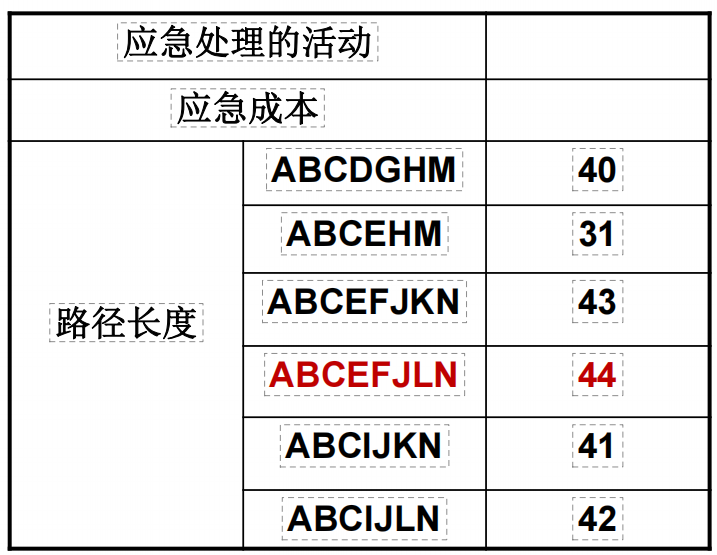
关键路径里面,J的边际成本最小,所以,我们先应急J一个周,总长度变为43,成本为30000:
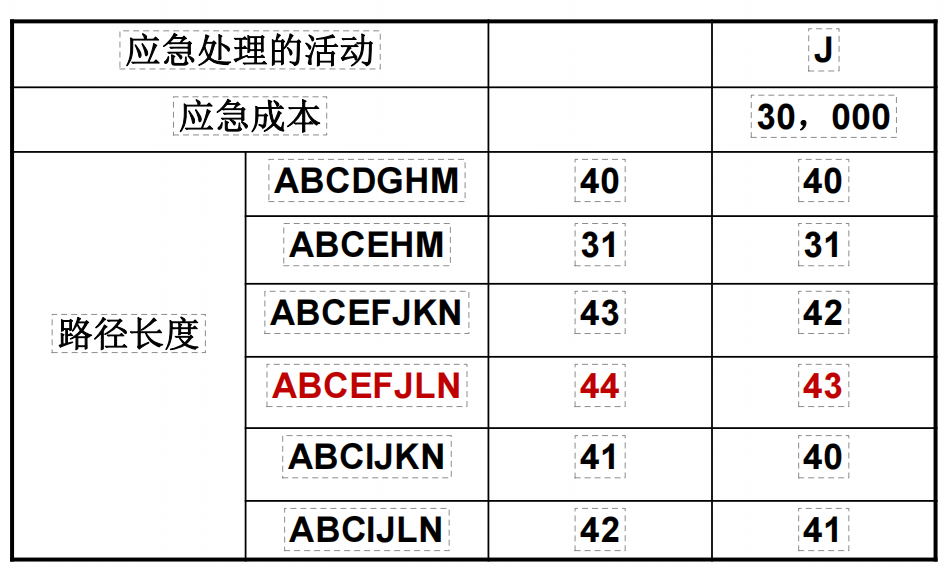
继续应急,还是选择J,所以,我们再应急J一个周,总长度变为42,成本再加30000:
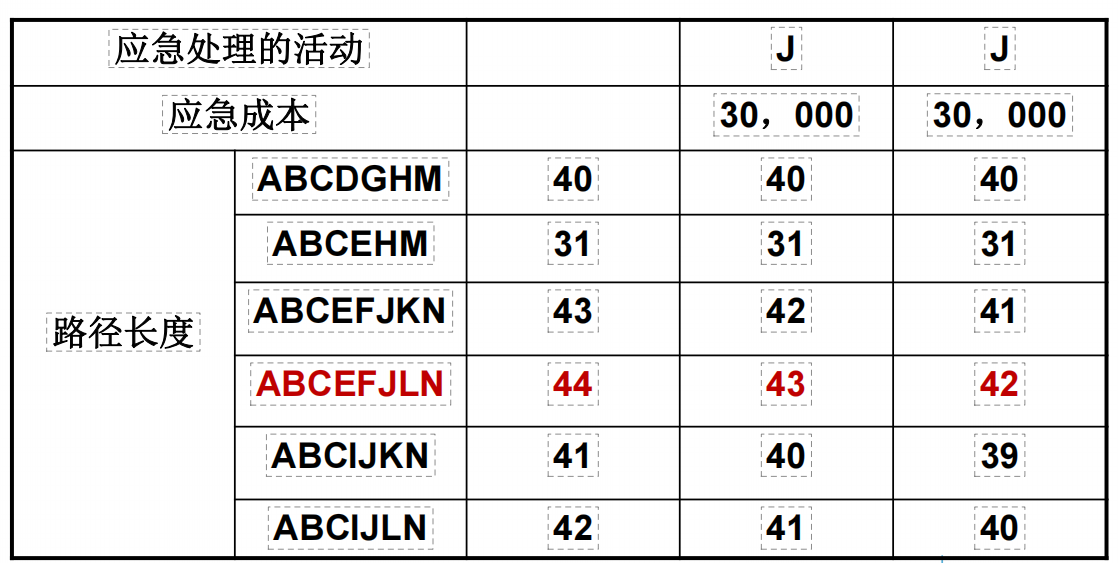
此时,J 可用于应急的时间已经耗尽,所以在关键路径上,继续找下一个边际成本最小的节点,也就是F。应急F一个周,关键路径总长度变为41,成本加40000:

继续应急 F 一个周,关键路劲总长度变为40,此时有了3条关键路径,并且达到了目标值的40周(小于等于目标值,就可以停下来了)。同时,这次的应急,成本需要再加40000:

以下为了解一下即可。 如果设计为线性规划,目标函数为使用的最低成本。约束条件为:
1、节约时间≤最大节约时间(每个工序节点);
2、项目完成时间≤要求的完成时间;
3、工序开始时间≥每个紧前工序的完成时间;
4、项目完成时间≥所有紧前工作的完成时间。
决策包括:
1、每个工序的开始时间;
2、应急后,每个工序的工期减少量;
3、项目的完成时间。
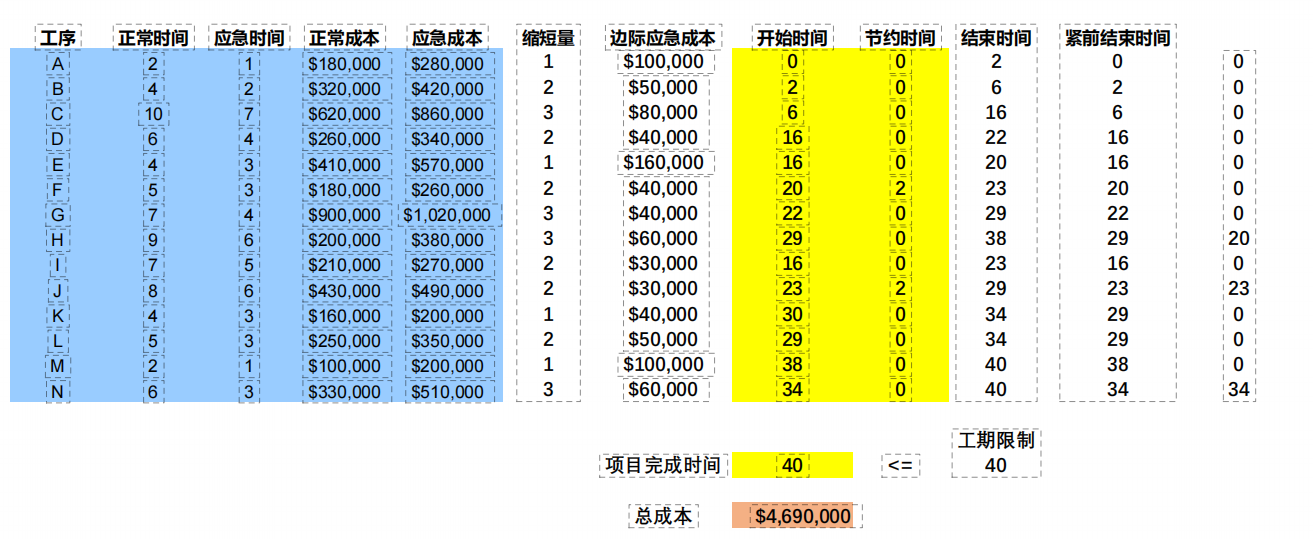
假设进一步问,要是可以在40周完成,就可以获得15w的奖励,我们是否可以冲刺一下?
根据新的工期,计算得到方差、概率的情况是,40周完成的概率,只有50%。这种情况下,我们应当反对启动使用额外的14w(3w+3w+4w+4w)进行应急。但是,这个计划完全不可用么?也不是,因为随着项目的推进,如果前期一直都非常顺利,甚至,还有很多提前,那么40w完成的概率,会不断提高。这时这个计划,也不是完全不可以。因此,这个计划,可以作为一个储备计划,并且,只有在节点F之前,所有的活动都进行的很好,才有使用这个计划的意义。(因为这次应急了两个节点,F和J,F是更靠前的。)
PERT/Cost成本监控
上述都是在一开始进行计算,那么项目过程中的监控应该怎么做呢?这时,可以使用PERT/Cost法。
1、当使用PERT/Cost时,假设完成一个活动需要的成本,在整个活动的工期内,是以固定的比率随时间上升的;
2、分别按最早开始、最晚开始计算成本线;
3、基于成本线进行实时监控。
假设,一个活动,按最早和最晚开始一时间,计划成本随时间的变化情况如下图所示。可以看到成本的花销上升速度不一样,可以假想一下,你越早开始,投入成本肯定多,但后期慢慢就投入少了。
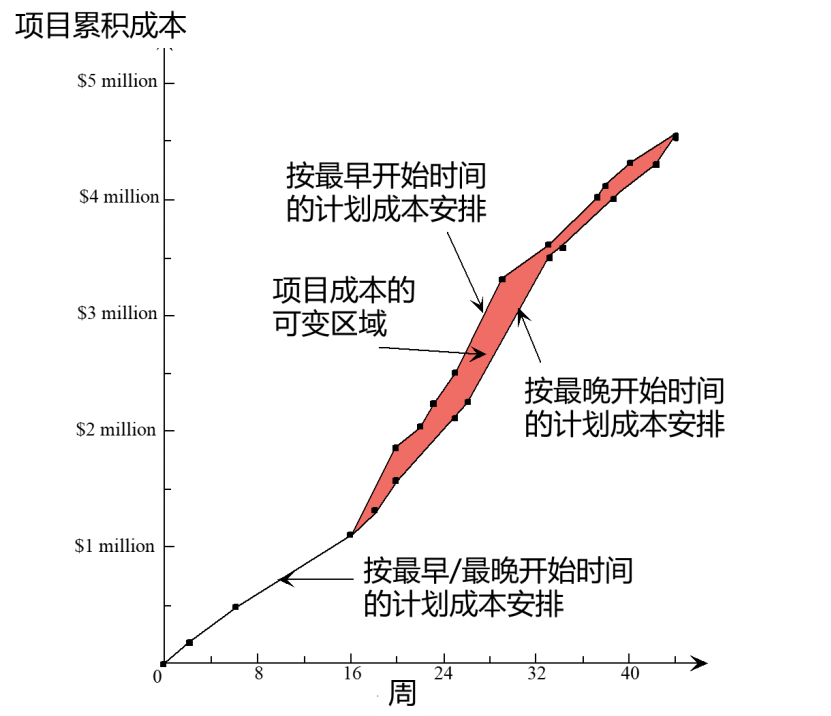
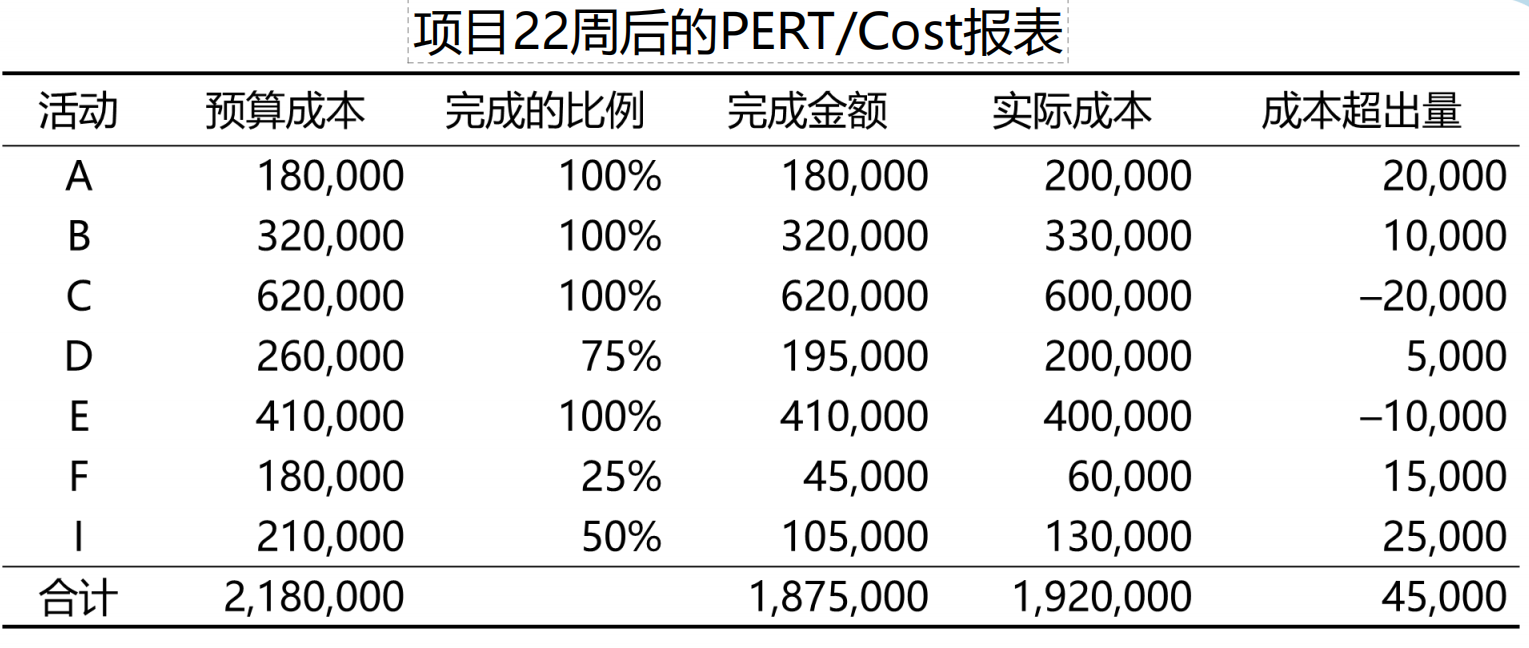
以下是一个PERT/Cost报表示例,可以基于这个,实时调整后续的投入策略。