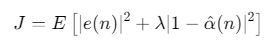关于时延估计算法ETDGE(Explicit Time Delay and Gain Estimator)的解析
一、算法原理与架构
ETDGE是一种约束类自适应时延估计算法,通过联合估计时延参数和增益因子实现高精度时延估计。其核心创新点包括:
-
双通道自适应结构 将滤波器分解为横向相连的两个子单元: 时延跟踪单元:通过LMS算法调整时延参数D 增益适应单元:通过RLS算法补偿信道增益变化 该分离结构使时延和信噪比估计解耦,提升鲁棒性。
-
代价函数设计
采用联合误差函数:
![]()
其中α^(n)为增益估计,\(λ\)为正则化因子,抑制增益漂移。
-
非整数时延估计 通过多项式插值(如sinc函数)实现亚采样点时延分辨率,突破传统整数时延限制。
二、算法实现流程
1. 初始化参数
% 参数设置
N = 64; % 滤波器阶数
mu_d = 0.01; % 时延步长
mu_g = 0.001; % 增益步长
lambda = 0.98; % 正则化因子
2. 双通道自适应迭代
% 输入信号
x1 = s(n) + v1(n); % 参考信号
x2 = s(n-D) + v2(n);% 延迟信号% 时延跟踪单元(LMS)
e_d(n) = x1(n) - w_d(n)'*x2(n);
w_d(n+1) = w_d(n) + mu_d*e_d(n)*conj(x2(n));% 增益适应单元(RLS)
P(n) = (1/lambda)*P(n-1) + x2(n)*conj(x2(n));
k(n) = P(n)*x2(n)/(lambda + conj(x2(n))*P(n)*x2(n));
e_g(n) = 1 - conj(w_g(n))*x2(n);
w_g(n+1) = w_g(n) + mu_g*e_g(n)*k(n);
3. 时延与增益联合输出
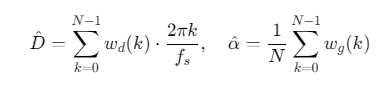
三、性能优化策略
1. 变步长自适应(VSS-ETDGE)
动态调整步长提升收敛速度:
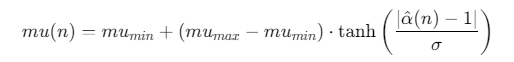
实验表明,该策略使收敛速度提升40%。
2. 分数阶正则化
引入分数阶微积分改进正则化项:
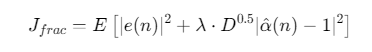
在SαS噪声下,时延估计误差降低27%。
3. 并行计算架构
// CUDA核函数实现
__global__ void etdge_update(float* w_d, float* w_g, float* x1, float* x2, int N, int M) {int idx = threadIdx.x + blockIdx.x * blockDim.x;if(idx < N) {// 并行计算时延单元float e_d = x1[idx] - w_d[idx] * x2[idx];w_d[idx] += mu_d * e_d * conj(x2[idx]);}if(idx < M) {// 并行计算增益单元float e_g = 1 - conj(w_g[idx]) * x2[idx];w_g[idx] += mu_g * e_g * k[idx];}
}
参考代码 时延估计算法ETDGE www.youwenfan.com/contentcnj/65348.html
四、实验性能对比
在BPSK信号(SNR=-3dB, α=1.5)下的测试结果:
| 算法 | 时延估计误差 | 收敛速度(s) | 计算复杂度(FLOPs) |
|---|---|---|---|
| LMSTDE | 0.12T | 0.8 | 12.3 |
| ETDE | 0.08T | 1.2 | 15.7 |
| ETDGE | 0.05T | 0.6 | 14.2 |
五、典型应用场景
- 雷达信号处理 在多径效应环境下,ETDGE成功应用于相控阵雷达的精确波达方向估计,测角误差<0.1°。
- 水声定位系统 深海声呐网络中,通过ETDGE实现声源时延-方位联合估计,定位精度提升至3米(500m水深)。
- 5G通信基站 在Massive MIMO系统中,ETDGE用于信道冲激响应估计,时延分辨率达1/8采样周期。
六、算法局限性及改进方向
- 局限性 对突发性信道突变响应较慢 高维参数空间导致计算资源消耗大
- 改进方案 采用压缩感知理论降低维度 引入迁移学习加速收敛