T1 舞蹈机器⼈
题目大意:
给一个可以向四个方向移动的小点,对于每次移动,如果上或下⽅向进⾏了⼀次移动,那么,下⼀次就只能往左或右⽅向进⾏⼀次移动,反之亦然。
求该点可以到达的位置数量。
STEP 1.
对于这个问题,我们可以想到一种非常暴力且优雅的 DFS 解法:
void dfs(int x,int y,int towards,int step){if(x < 0 || x >= n || y < 0 || y >= m) return; // 越界if(step==n){arr[x][y]++; // 到达位置}if(towards==0){ // 左右dfs(x-1,y,1,step+1);dfs(x+1,y,1,step+1);}else{ // 上下dfs(x,y-1,0,step+1);dfs(x,y+1,0,step+1);}
}
int main(){/*其他内容*/dfs(501,501,0,0); //从中间开始dfs(501,501,1,0);int ans=0;for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(arr[i][j]) ans++; // 统计到达位置的数量}}cout<<ans;return 0;
}
喜提 \(60\space pts\)!
STEP 2.
言归正传,这其实是一道数学题。
对于 \(n\) 为偶数时,对于整个的移动过程⽽⾔,每两次移动就相当于是在正⽅形的对⻆线上移动了⼀次(即斜着⾛了⼀步),我们可以发现其能够到达的地方其实就是一个边长为 \(n/2+1\) 的正方形。
例如,在 \(n=4\) 时,图中所标记的蓝色点即为可到达的点
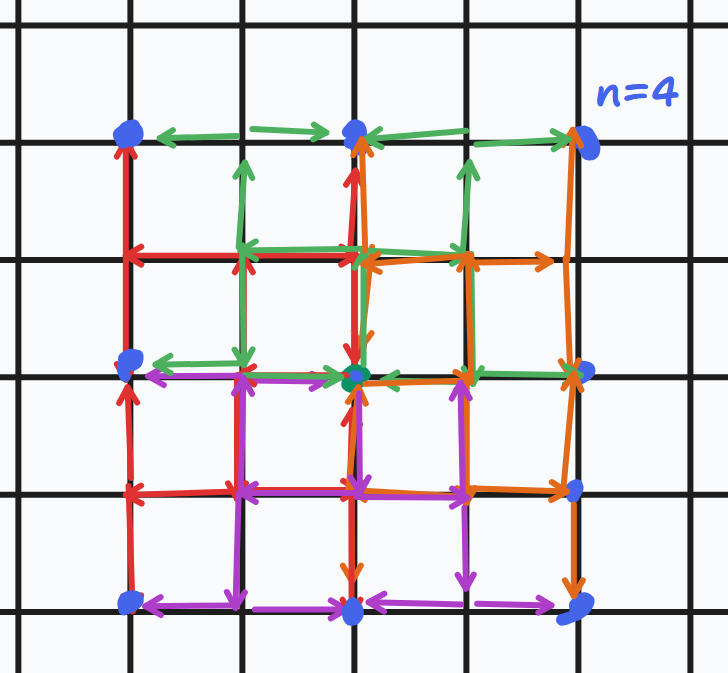
对于 \(n\) 为奇数时,我们可以发现其能够到达的地方其实就是两个长为 \(n/2+1\) 宽为 \(n/2+2\) 的长方形构成的。
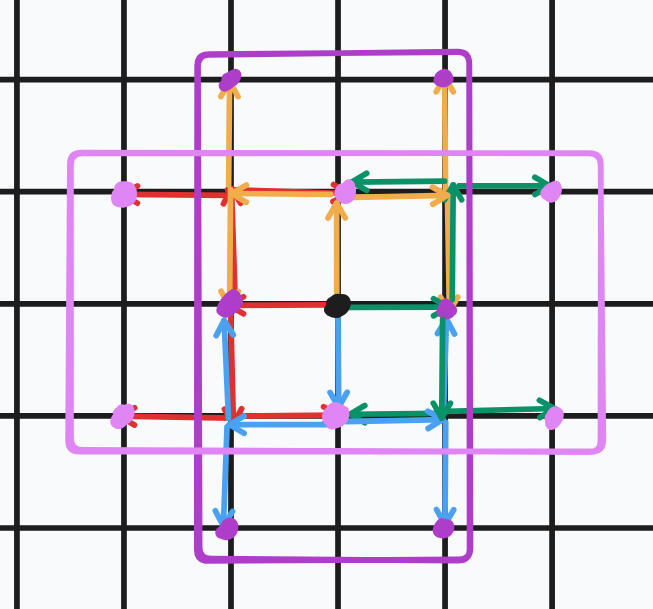
STEP 3.
因此,我们可以根据 \(n\) 的奇偶性,来获得最终答案
\( ans=\begin{cases} (n/2+1)^2&n\space mod\space 2=0\\ 2\times(n/2+1)\times(n/2+2)&n\space mod\space 2=1 \end{cases} \)
代码
#include<bits/stdc++.h>
using namespace std;
int main(){int n;cin>>n;if(n&1){ // n 为奇数cout<<2*(n/2+1)*(n/2+2);}else{ // n 为偶数cout<<(n/2+1)*(n/2+1);}return 0;
}
