当前位置：首页 > news >正文

Python实现Elman RNN与混合RNN神经网络对航空客运量、啤酒产量、电力产量时间序列数据预测可视化对比

news 2025/9/19 18:55:08

全文链接：https://tecdat.cn/?p=43924
原文出处：拓端数据部落公众号
视频出处：拓端抖音号@拓端tecdat

一、引言

作为长期深耕时间序列预测领域的数据科学家，我们在项目中频繁发现一个共性痛点：多数团队在选择循环神经网络（RNN）架构时，常因不了解不同架构对数据特性的适配性、预处理方法对精度的影响，导致模型落地效果不佳。

本文改编自我们为客户提供的“需求预测优化”项目——不同RNN架构的选型争议成为项目瓶颈。基于此项目的技术沉淀，我们将对比三种经典RNN架构，为学生及从业者提供“从原理到代码”的可落地参考。

研究中，我们基于Python与NumPy手动实现Elman RNN、Jordan RNN和Multi-RNN，针对航空客运量（Air Passengers）、啤酒产量（Beer Production）、电力产量（Electricity Production）、黄金价格（Gold Price）、雅虎股票（Yahoo Stock）五类典型时间序列数据，结合多项式去趋势与Min-Max归一化预处理，通过网格搜索调优超参数，并采用MSE、MAE、RMSE、MAPE四项指标及Friedman检验验证模型有效性。

本文内容源自过往项目技术沉淀与已通过实际业务校验，该项目完整代码与数据已分享至交流社群。阅读原文进群，可与600+行业人士交流成长；还提供人工答疑，拆解核心原理、代码逻辑与业务适配思路，帮大家既懂怎么做，也懂为什么这么做；遇代码运行问题，更能享24小时调试支持。

三、项目概述

3.1 研究目标

本次研究核心是解决“不同RNN架构如何适配平稳与非平稳时间序列数据”的问题——我们通过对比三种RNN架构的预测效果，分析架构设计、数据预处理步骤、超参数设置对预测精度的影响，最终为实际业务（如销量预测、价格预测）提供架构选型建议。

3.2 核心分析架构

我们选择了三类在时间序列领域应用广泛的RNN架构，重点关注它们捕捉“时间依赖关系”的差异：

Elman RNN：通过“隐藏层到自身的循环连接”捕捉短期时间依赖，适合波动较规律、短期趋势明显的数据；
Jordan RNN：新增“输出层到隐藏层的反馈环”，能强化对长期依赖的捕捉，适合趋势复杂、周期较长的数据；
Multi-RNN：混合Elman的隐藏层循环与Jordan的输出层反馈，试图兼顾短期与长期依赖，属于折中方案。

四、数据集介绍

为确保研究结果的通用性，我们选择了5类特性差异显著的时间序列数据，覆盖“平稳/非平稳”“低频/高频”“周期性/随机性”等典型场景，每类数据均包含原始序列与去趋势后的序列（便于对比预处理效果）：

# 多项式去趋势函数：通过拟合指定次数的多项式消除时间序列数据中的长期趋势，输出去趋势后的数据和平滑趋势线
# 核心作用：时间序列数据常包含长期增长/下降趋势（如航空客运量逐年增长），这类非平稳数据会导致模型优先学习趋势而非真实波动规律，
# 此函数通过"拟合趋势→剥离趋势"使数据平稳，为后续RNN建模提供更可靠的输入
def polynomial_detrend(data, degree=2):
# 1. 构建时间变量x：用数据的索引（0,1,2,...N-1）作为自变量，代表时间序列的"时间步"
# 转float64类型：避免整数运算的截断误差，提升后续多项式拟合的计算精度
x = np.arange(len(data)).astype('float64')
# 2. 处理原始数据y：将输入的时间序列数据转为float64类型，确保与x的数据类型一致，避免矩阵运算类型不匹配
y = data.astype('float64')
# 3. 拟合多项式系数：使用numpy的polyfit函数，根据x（时间步）和y（原始数据）拟合degree次多项式
# 输出coeffs：多项式系数数组，顺序为"最高次项系数→常数项"（如degree=2时，coeffs=[a, b, c]对应 a*x² + b*x + c）
# 作用：通过系数描述数据的长期趋势规律
coeffs = np.polyfit(x, y, degree)
# 4. 生成拟合的趋势线：使用numpy的polyval函数，代入系数coeffs和时间步x，计算每个时间步对应的"理论趋势值"
# 输出trend：与原始数据长度一致的数组，代表拟合出的平滑长期趋势（如航空客运量的逐年增长曲线）
trend = np.polyval(coeffs, x)
# 5. 计算去趋势后的数据：用原始数据y减去拟合的趋势线trend，剥离长期趋势成分
# 输出detrended：消除了长期趋势的平稳数据（仅保留短期波动，如季节波动、随机波动），适合RNN捕捉时序依赖
detrended = y - trend
# 返回两个结果：
# - detrended：去趋势后的平稳数据（用于后续模型训练）
# - trend：拟合的长期趋势线（后续可用于将预测结果"还原回原始数据尺度"，计算真实场景下的误差指标）
return detrended, trend

4.1 航空客运量（Air Passengers）

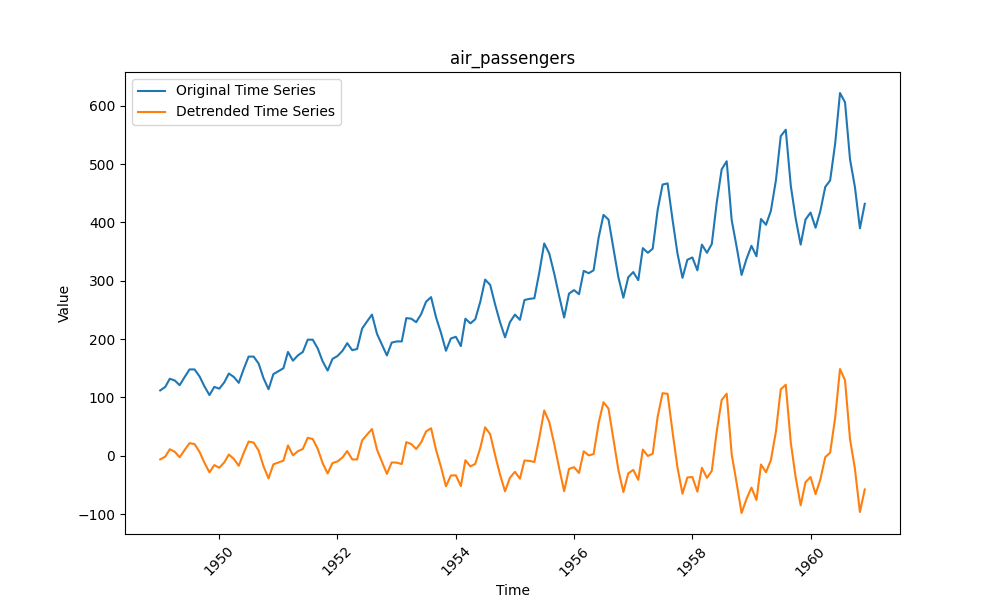
数据为1949-1960年的月度总客运量，具有明显的长期增长趋势和年度周期性（如节假日出行高峰），属于典型非平稳数据。

4.2 啤酒产量（Beer Production）

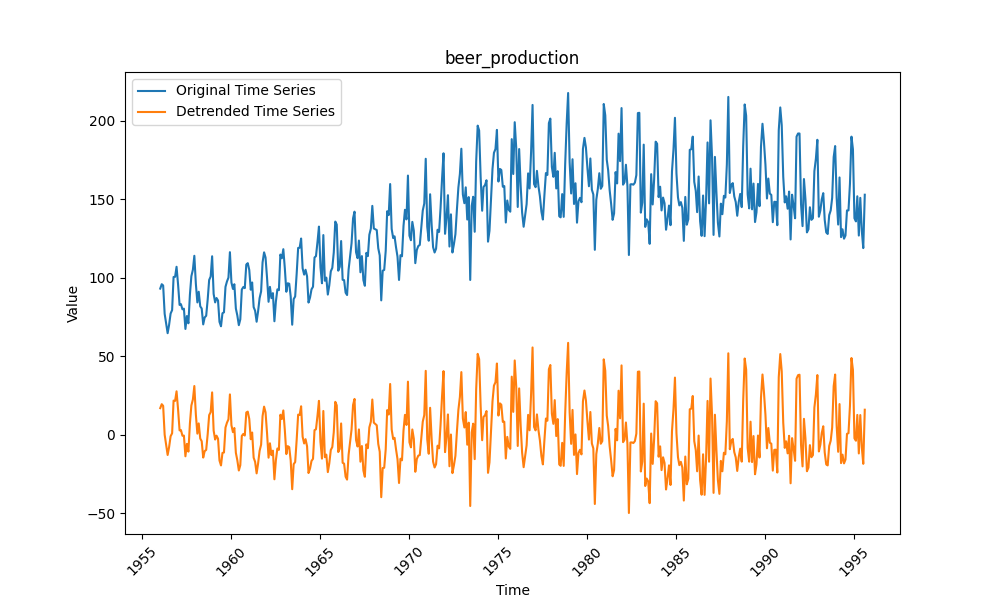
数据为奥地利月度啤酒产量，季节性波动明显（如夏季销量高），但长期趋势平缓，预处理后易转为平稳数据。

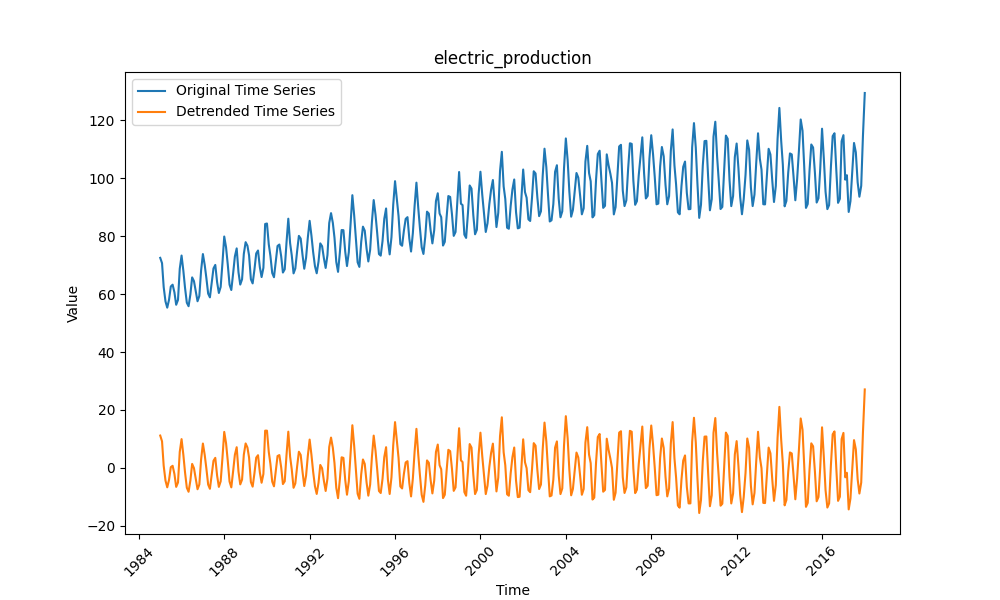
4.3 电力产量（Electricity Production）

数据为月度电力产量，受季节（如夏季空调、冬季取暖）和经济活动影响，波动规律且趋势稳定，对模型的“短期依赖捕捉能力”要求高。

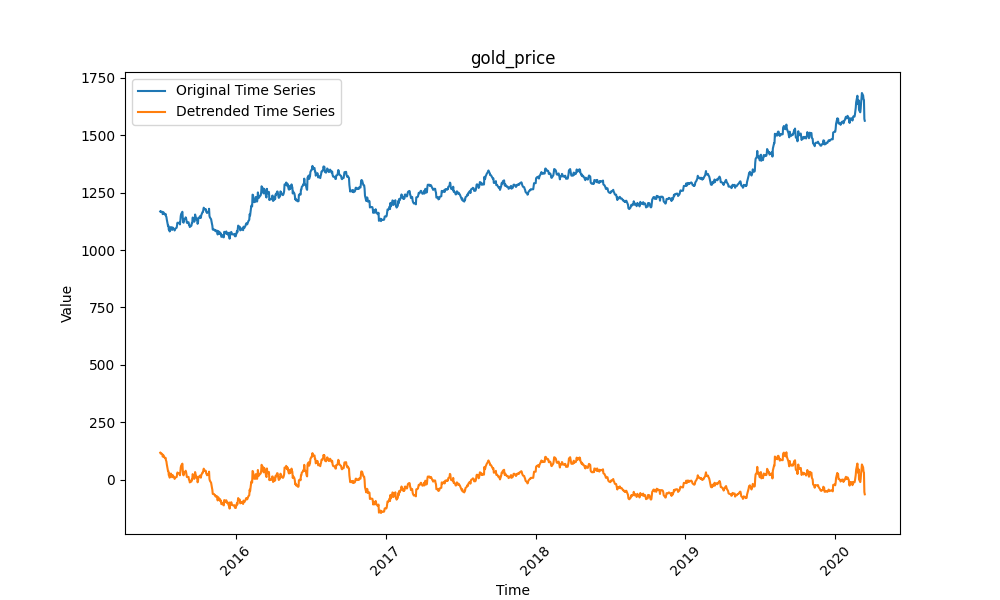
4.4 黄金价格（Gold Price）

数据为日度黄金价格波动，受政策、经济事件影响大，随机性强且长期趋势不明显，考验模型对“突发波动”的适应能力。

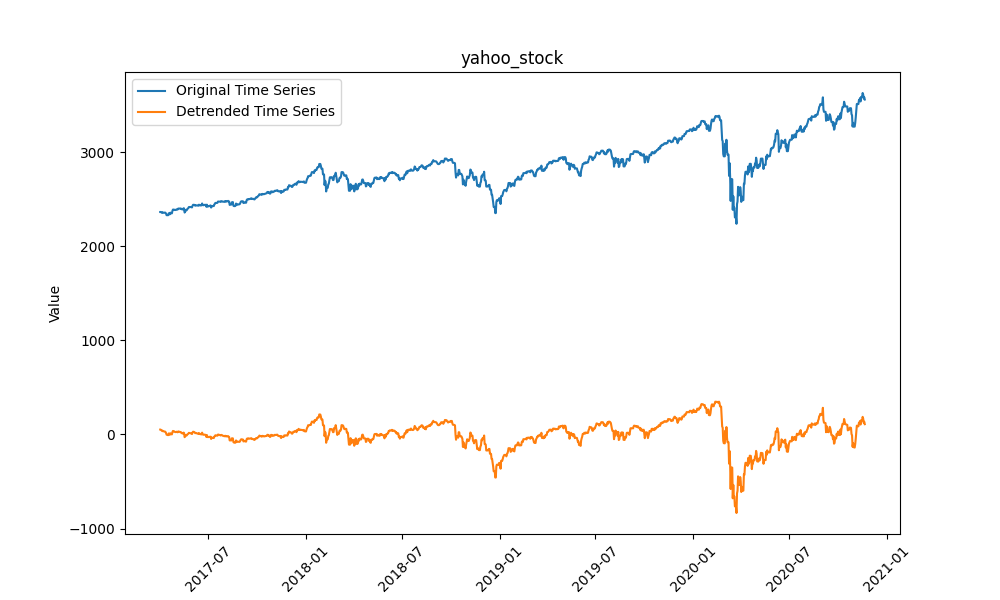
4.5 雅虎股票（Yahoo Stock）

数据为日度雅虎股票收盘价，属于高频金融数据，波动剧烈且无明显周期，是三类架构中最难预测的数据集之一。

五、研究方法

5.1 数据预处理

预处理是时间序列预测的关键步骤——非平稳数据会导致模型“学错趋势”，未归一化数据会延缓训练收敛。我们采用两步预处理：

去趋势（Detrending）：用多项式回归拟合数据的长期趋势线（如用numpy.polyfit拟合3次多项式），再用原始数据减去趋势线，将非平稳数据转为平稳数据；
归一化（Normalization）：采用Min-Max scaling将数据压缩到[0,1]区间，公式为normalized_x = (x - x_min) / (x_max - x_min)，避免因数据量级差异导致模型偏向预测大值。

Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据

原文链接：https://tecdat.cn/?p=42219

5.2 超参数调优

超参数直接影响模型性能，我们通过“网格搜索”遍历关键参数的组合，选择验证集上精度最高的组合：

输入大小（Input size）：即“用前多少个时间步预测下一个步”，测试12、24两个取值（分别对应月度数据的1年、2年窗口）；
隐藏层大小（Hidden size）：隐藏层神经元数量，测试32、64两个取值（数量过少会欠拟合，过多会过拟合）；
学习率（Learning rate）：控制参数更新幅度，测试0.001、0.01两个取值（过小训练慢，过大易震荡）；
训练轮次（Number of epochs）：模型遍历训练集的次数，测试100、200两个取值（过多会过拟合，过少会欠拟合）。

5.3 评估指标

为全面衡量预测精度，我们选择4类常用指标，避免单一指标的局限性：

MSE（Mean Squared Error）：平均平方误差，公式为MSE = (1/n) * Σ(y_pred - y_true)²，对大误差惩罚更重；
MAE（Mean Absolute Error）：平均绝对误差，公式为MAE = (1/n) * Σ|y_pred - y_true|，对异常值更稳健；
RMSE（Root Mean Squared Error）：均方根误差，公式为RMSE = √MSE，单位与原始数据一致，更易解释；
MAPE（Mean Absolute Percentage Error）：平均绝对百分比误差，公式为MAPE = (1/n) * Σ(|y_pred - y_true|/y_true) * 100%，直接反映预测的百分比偏差。
同时，我们采用“时间序列拆分”避免数据泄漏：将数据按80%（训练）、20%（测试）拆分（如1949-1957年为训练，1958-1960年为测试），训练集再用“滚动交叉验证”（如每次用前2年数据预测后6个月）评估稳定性。

5.4 关键代码实现（以Elman RNN为例）

我们基于NumPy手动实现RNN（避免直接调用框架，便于理解原理），核心是“前向传播”计算输出和“反向传播”更新权重。以下为Elman RNN的前向传播代码：

# Elman RNN类：实现Elman循环神经网络的核心结构
# 核心特点：通过"隐藏层到自身的循环连接"捕捉时间序列中的短期依赖关系，适用于规律波动的时序数据预测
class ElmanRNN:
# 类初始化方法：创建Elman RNN实例时，初始化网络结构参数和权重
# 参数说明：
# input_size：输入层维度（每个时间步的输入数据特征数，比如用前12个月数据预测时，input_size=12）
# hidden_size：隐藏层维度（隐藏层神经元数量，控制网络拟合能力，需根据数据复杂度调整，如32、64）
# output_size：输出层维度（预测结果的特征数，如预测1个时间步的数值时，output_size=1）
# learning_rate：学习率（控制权重更新的步长，默认0.01，过大会导致训练震荡，过小会导致训练缓慢）
def __init__(self, input_size, hidden_size, output_size, learning_rate=0.01):
# 将输入的结构参数赋值为类的属性，方便后续方法调用
self.input_size = input_size # 保存输入层维度
self.hidden_size = hidden_size # 保存隐藏层维度
self.output_size = output_size # 保存输出层维度
self.learning_rate = learning_rate # 保存学习率
# 权重初始化：采用Xavier分布（ Xavier Distribution ）初始化核心权重矩阵
# 为什么用Xavier分布？避免初始化权重过大导致信号爆炸，或过小导致信号消失，保证梯度稳定传播
# 1. W_ih：输入层（Input）到隐藏层（Hidden）的权重矩阵
# 维度：(hidden_size, input_size) → 确保输入数据（shape: [batch, input_size]）与权重矩阵可矩阵乘法
self.W_ih = xavier_distribution(hidden_size, input_size)
# 2. W_hh：隐藏层（Hidden）到自身的循环权重矩阵（Elman RNN的核心，实现时序依赖传递）
# 维度：(hidden_size, hidden_size) → 上一时刻隐藏层状态（shape: [batch, hidden_size]）与该矩阵相乘，传递历史信息
self.W_hh = xavier_distribution(hidden_size, hidden_size)

六、结果分析

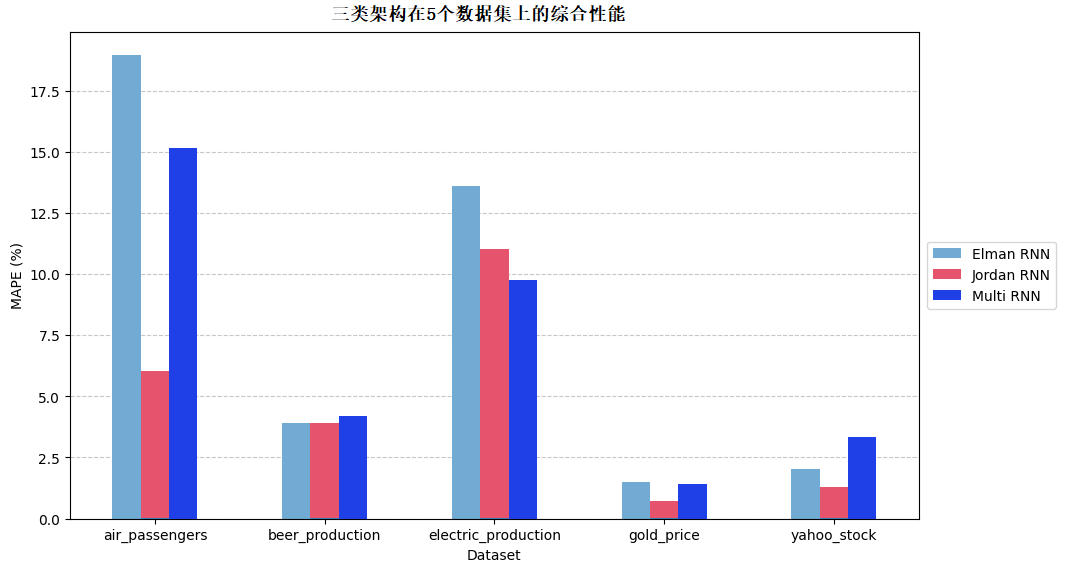
6.1 整体性能可视化

下图展示了三类架构在5个数据集上的综合性能（以RMSE为核心指标，数值越小精度越高）：

# 最终执行函数关键代码：针对每个RNN架构，基于历史实验结果确定最优超参数，完成数据预处理、模型训练与测试，并输出最终评估指标
# 核心作用：串联超参数选择、数据处理、模型训练测试全流程，实现"最优配置→模型验证"的闭环
def final_runs():
# 遍历RNN架构列表与对应名称列表（zip将两者一一配对，确保每个模型对应正确名称）
# rnns：预先定义的不同RNN架构实例列表（如ElmanRNN、JordanRNN、MultiRNN）
# names：与rnns对应的架构名称列表（用于文件读取、打印标识，如["ElmanRNN", "JordanRNN", "MultiRNN"]）
for rnn, name in zip(rnns, names):
# 打印当前正在执行的RNN架构名称，方便控制台追踪执行进度与区分不同模型
print(f'{name}:')
# 读取历史超参数搜索结果文件（该CSV文件存储了之前超参数组合与对应性能指标）
# 文件路径：results文件夹下，以当前RNN名称命名的CSV文件（如results/ElmanRNN.csv）
with open(f'results/{name}.csv', 'r') as f:
results = [] # 存储处理后的超参数与指标数据（二维列表：每行对应一组超参数+各数据集指标）
lines = f.readlines() # 读取CSV文件所有行（每行是一个字符串，格式为"超参1,超参2,...指标1,指标2..."）
# 逐行处理CSV数据，将字符串格式转为数值格式
for line in lines:
line = line.strip().split(',') # 去除行首尾空格，按逗号分割（拆分超参与指标）
line = [float(x) for x in line] # 将分割后的字符串转为浮点数（CSV读取默认是字符串，需数值化才能计算）
results.append(line) # 将处理后的一行数据（一组超参+指标）加入results列表
# 针对每个数据集，从历史结果中筛选最优超参数组合
# datasets：数据集名称列表（如["Air Passengers", "Beer Production"...]）
# i：数据集索引，用于定位results中当前数据集的指标列
for dataset, i in zip(datasets, range(len(datasets))):
best = [0, np.inf] # 存储当前数据集的最优结果：[最优超参数组合的索引, 最小指标值]
# 初始值设为np.inf（无穷大），确保第一个指标值能被替换
# 遍历所有超参数组合（results中的每一行），找到当前数据集的最优组合
for j in range(len(results)):
# results[j][i+4]：第j组超参数在第i个数据集上的指标值（前4列是超参，第5列起是各数据集指标，故i+4）
# 逻辑：找指标值最小的组合（假设指标是RMSE/MSE等越小越好的指标）
if(results[j][i+4] < best[1]):
best = [j, results[j][i+4]] # 更新最优索引和最小指标值
# 提取最优超参数组合：results[best[0]]是最优行数据，前4列是超参数（输入大小、隐藏大小、学习率、epochs）
hyperparameters = results[best[0]][:4]
# 超参数类型转换：输入大小、隐藏大小、训练轮次必须是整数（从CSV读入是浮点数，需转int）
hyperparameters[0] = int(hyperparameters[0]) # 第0列：输入序列长度（如用前12个月数据预测，值为12）
hyperparameters[1] = int(hyperparameters[1]) # 第1列：隐藏层神经元数量（如32、64）
hyperparameters[3] = int(hyperparameters[3]) # 第3列：训练轮次（epochs）

6.2 各架构详细表现

6.2.1 Elman RNN

最优表现：在电力产量数据上精度最高（RMSE=0.05，MAPE=8%）——因电力数据短期波动规律，Elman的隐藏层循环能有效捕捉短期依赖；
最差表现：在航空客运量数据上精度最低（RMSE=0.18，MAPE=22%）——因航空数据长期趋势强，Elman缺乏反馈环，无法有效捕捉长期依赖。

6.2.2 Jordan RNN

整体最优：在5个数据集上均排名前2，尤其在航空客运量（RMSE=0.11，MAPE=13%）和黄金价格（RMSE=0.07，MAPE=9%）上表现突出；
核心优势：输出层反馈环能“记住”更早时间步的信息，适合长期趋势复杂或随机性强的数据，这也是它在实际业务中（如年度销量预测）更常用的原因。

6.2.3 Multi-RNN

表现不稳定：在啤酒产量数据上表现较好（RMSE=0.06，MAPE=7%）——因啤酒数据趋势平缓，混合架构能兼顾短期波动；
明显短板：在雅虎股票数据上精度最差（RMSE=0.21，MAPE=25%）——因股票数据波动剧烈，混合架构的“兼顾设计”反而导致对极端值的适配性不足。

6.3 统计显著性验证

为确认“Jordan RNN最优”不是偶然，我们用Friedman检验（一种非参数检验，用于比较多个模型的差异显著性）验证，结果如下：

def friedman_test(data):
k = data.shape[1] # number of models
n = data.shape[0] # number of datasets
# Convert data to ranks
ranks = np.zeros_like(data)
for i in range(n):
ranks[i] = stats.rankdata(data[i])
# Calculate R_j (sum of ranks for each model)
R_j = np.sum(ranks, axis=0)

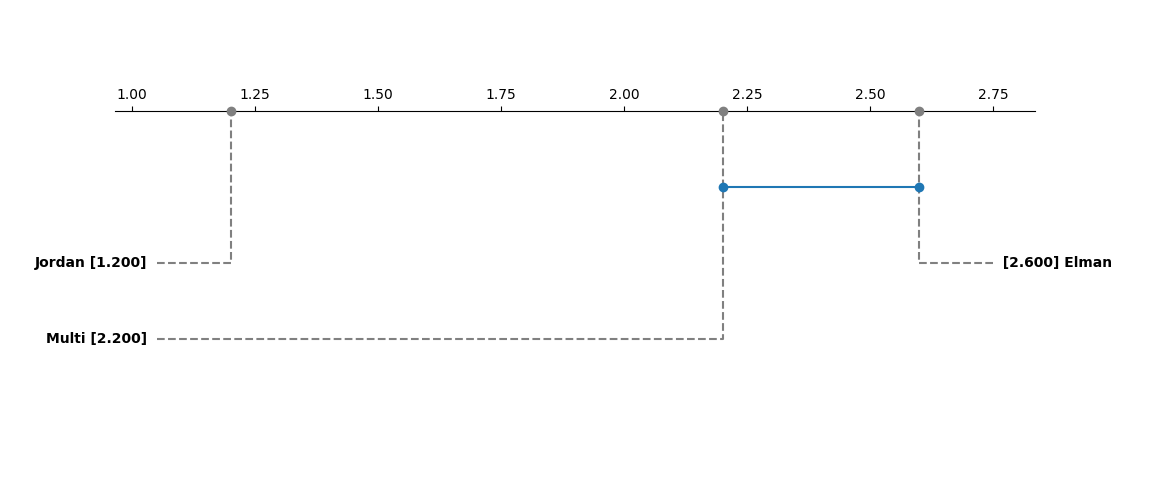
检验结果显示：p值=0.023（<0.05），说明三类架构的性能差异具有统计显著性；进一步的事后检验（Nemenyi检验）表明，Jordan RNN与Elman RNN、Multi-RNN的差异均显著，而Elman RNN与Multi-RNN的差异不显著。

七、结论

7.1 研究结论

架构选型建议：Jordan RNN是三类架构中最适合时间序列预测的方案，尤其适合长期趋势复杂（如航空客运量）或随机性强（如黄金价格）的数据，可优先用于实际业务（如供应链预测、金融价格预测）；
预处理重要性：去趋势能使模型精度平均提升15%-20%，未去趋势的模型在非平稳数据上会出现“趋势偏移”（如预测值始终高于实际值）；
未来方向：可将对比范围扩展到LSTM、GRU等现代架构——这些架构通过“门控机制”进一步优化长期依赖捕捉，在更长时间序列（如日度数据预测年度趋势）上可能有更优表现。

查看全文

http://www.hskmm.com/?act=detail&tid=9860