咕掉好几场墨泥塞的僵尸来颓题解惹
因为想等大 ~蛇 ~们 ~改完之后再改(根本不会)
rt:
你说这是吃薯片-S?
我还是跳楼来的比较快。
这题太**的神秘了,看上去都可做实际上(我)都写不出来。
sssssssssssssad。
A. 集合
题面link
开题!T1就是图论吗?T1就是图论吗?T1就是图论吗?T1就是图论吗?T1就是图论吗?T1就是图论吗?T1就是图论吗?
不是,T1是个结论!!!!!!
哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈
咳咳。
赛时
手玩2.5h,发现一个神秘的性质:
rt:
将1,2结盟
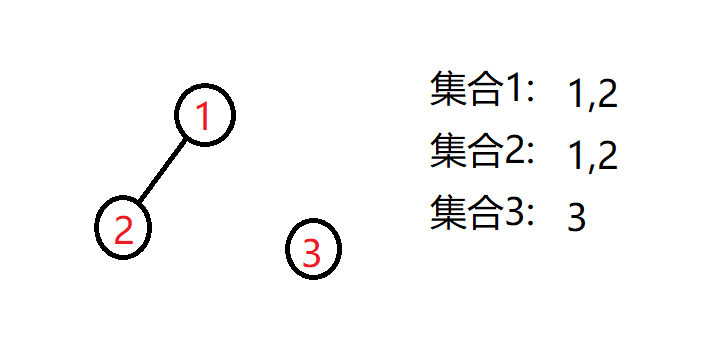
将1,3结盟
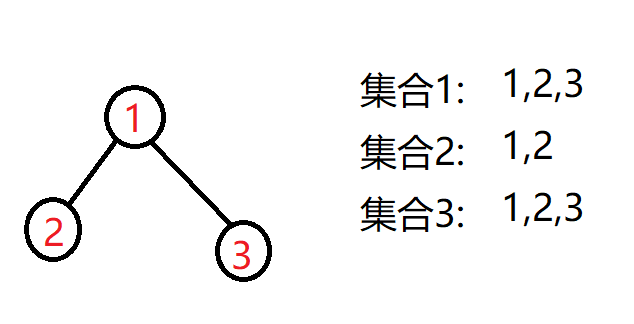
将1,2结盟

发现在\(1,2,3\)随意连边,发现最大的集合大小为连通块大小,然后你考虑非最大的集合,发现其可以通过过倒着遍历加边来处理集合大小。
然后。。
发现你不能合理的处理这个东西
死了。┏┛墓┗┓...(((m-__-)m
赛后
根据题解可知:
若你倒着按输入连边,可以得到 \(i\) 出现在哪些集合里面(手玩一下可得),且与集合大小是相等的,然后你打开高一数学课本,发现:
然后可以发现,若你连一个边,可能会有以下两种情况:
- 之前这条边没有被连过
那这两个集合一定没有公共元素,所以它们两个的交集大小是他们的大小之和。连完之后可得两个集合的交集大小是它们的集合大小 - 之前这条边有被连过
那这两个集合一定有公共元素,所以它们两个的交集大小是他们的大小之和减去他们的并集大小。
考虑他们的并集大小就是上一次连这条边得到的集合大小。
好!然后就模拟一下啊!
代码
#include<bits/stdc++.h>
using namespace std;
int x[400010],y[400010];
int to[400010],siz[400010],last[400010];
bool vis[400010];
int main()
{freopen("set.in","r",stdin);freopen("set.out","w",stdout);int n,m;cin>>n>>m;for(int i=1;i<n;i++){cin>>x[i]>>y[i]; } for(int i=1;i<=m;i++){cin>>to[i];}for(int i=1;i<=n;i++){siz[i]=1;}for(int i=m;i>=1;i--){int js=to[i];if(vis[js]==0){siz[x[js]]=siz[y[js]]=siz[x[js]]+siz[y[js]];last[js]=siz[x[js]];}else{siz[x[js]]=siz[y[js]]=siz[x[js]]+siz[y[js]]-last[js];last[js]=siz[x[js]];}vis[js]=1;}for(int i=1;i<=n;i++){cout<<siz[i]<<" ";}return 0;
}
